DS博客作业05——树
1.本周学习总结 
1.1思维导图
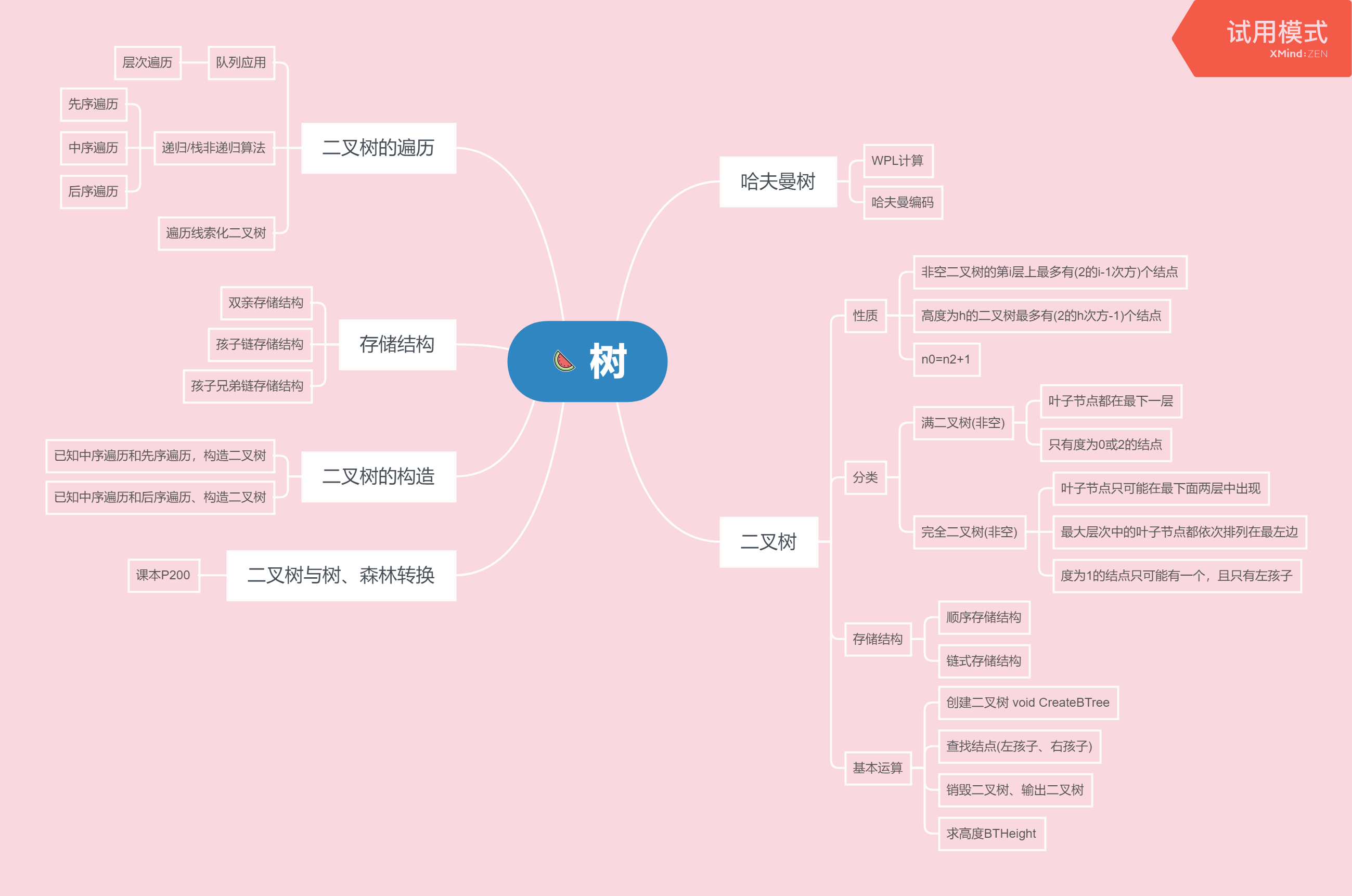
1.2学习体会
- 学习:相比于之前的数据结构,树多了很多性质,相应的也多了很多计算题,不得不说,专有名词也是颇多。觉得树最独特的地方就是它的兄弟、孩子结点,用以组成了它独特的树状结构,其他部分则是对于前面所学习知识点的复习以及再应用,即递归算法、顺序存储结构、链式存储结构、栈、队列。
- 体会:递归算法虽然代码量非常少,容易编写,但是必须得完全明白整个递归过程,一旦出现错误,我觉得不是很容易找到,pta的日常练习因为概率考试有些耽误,几乎是在上机考试之前才刚好做完,上机测试中,考的很差,每道题都有基本写出来,但都存在大大小小的疏忽,有了错误检查很久都没有找出来,还是对于递归算法比较生疏,而且发现了自己对于形参的传递这一块知识点有些模糊,要再进行复习巩固。
2.PTA实验作业 
说明:由于在日常提交列表中调试过程以及碰到的问题不太明显,所以将上机考试中的困难点列出
2.1.题目1:表达式树
输入一行中缀表达式,转换一颗二叉表达式树,并求解.

2.1.1设计思路
【建立二叉表达式树】
#建立字符栈op&&树根栈tree
op.push('#')
#遍历 str[i]
- if 是数字
依次存入树根栈内
- if 是符号
判断 str[i] 与 op栈顶的优先级
if str[i] 低于 栈顶
T->data为op栈顶符号,右、左子树为先后取tree栈顶元素
T入栈且op栈顶出栈
if str[i] 高于 栈顶
str[i]入栈
if str[i] 等于 栈顶
栈顶出栈
#栈顶元素不为’#‘
同 str[i] 低于 栈顶优先级
【计算表达式结果】
# if T不空
if 无左右子树即叶子结点 //递归口
return T->data
else
x= EvaluateExTree(左子树)
y=EvaluateExTree(右子树)
判断符号进行相应四则运算
“注意” 判断分母为零时
2.1.2代码截图


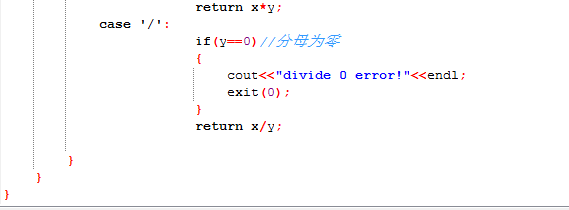
2.1.3本题PTA提交列表说明。

说明:
感觉PTA习题提交列表没有很准确,因为当时是在老师上完课之后就敲上去的,比较流畅,但是到了上机考试的时候还是 有很多小bug
- bug 1:当遍历字符数组str[i]时,栈顶元素优先级高于字符时,T->data应该取的是栈顶元素,而不是str[i];
- bug 2:将str[i]入栈时代码应为op.push(str[i++]),而不是手滑成op.push(i++);
- bug 3: 计算结果函数中忽略了递归出口,以至于大体结构都有写出来,但是还是没有发现致命bug
- 总结:在树的程序编写之中,应该更加细心,尤其是在建树结束之后,不应该急于写应用函数,而是应该先检查建树是否成功,否则后面函数再完整也没啥用,表达式相关的题一直是我的一个弱点区,还是得多熟练熟练
2.2 题目2:算出二叉树所有叶子结点的带权路径长度和
二叉树叶子结点的带权路径长度指:叶子结点的权重路径长度。本题要求算出二叉树所有叶子结点的带权路径长度和
2.2.1设计思路
【递归建树】
Create(i,str)
- i从0开始
- if i > 字符串长度,即建树完毕 || str[i]为’#‘
return NULL //递归口
- else
T->data = str[i]
左子树=Create(2*I,str)
右子树=Creta(2*i+1,str)
return T
【计算带权路径长度和】
####形参为T和高度h以及引用wpl
- if 是空树
return
- else
if 是叶节点
wpl+=h*(T->data-'0')
else
h++;
递归(左子树,wpl,h);
递归(右子树,wpl,h);
2.2.2代码截图


2.2.3本题PTA提交列表说明。

说明:
- bug 1:这道题在练习过程中没有什么问题,但是在上机考试中,在计算wpl的函数上,出现了很大的误区,在递归的过程中我的代码明显会让整个程序崩溃,开始觉得这道题没有很难,就只是单纯靠着记忆,没有真正区看它整个递归的过程,以至于我的递归函数写成了 T->lchild=GetWpl(T,wpl,h),右子树也是如此,当时没有发现任何不对,现在看看确实是很荒唐了;
- bug 2:递归建树中,如若左子树递归的是2i,右子树递归的是2i+1,那么i应该从1开始而不是从0开始
- 总结:递归函数虽然代码量少,考试靠记忆问题也不大,但还是不能投机取巧,还是要明白整个递归过程,不然记忆过程除了纰漏,当下很难找出问题所在
2.3 题目3:输出二叉树每层节点
层次遍历树中所有节点。输出每层树节点。
2.3.1设计思路
【递归法建树】
略
【层次遍历】
void Level(BTree T)
# 新建队列q
- level表示层数,flag作为判断标志——初始化为0
curNode作为前指针,last作为后指针——初始化为T
- if 空树
输出NULL,return
else
T入队
# 遍历队列 while(队列不空)
- if curNode == lastNode //遍历一层结束
level++
if flag==0 即第一层
cout<< 层数:
flag=1;
else
cout<<endl再输出层数:
lastNode=队尾
curNode=队首
输出curNode->data
- if 左或右子树不空
左或右子树进队
- 队首出队
2.3.2代码截图
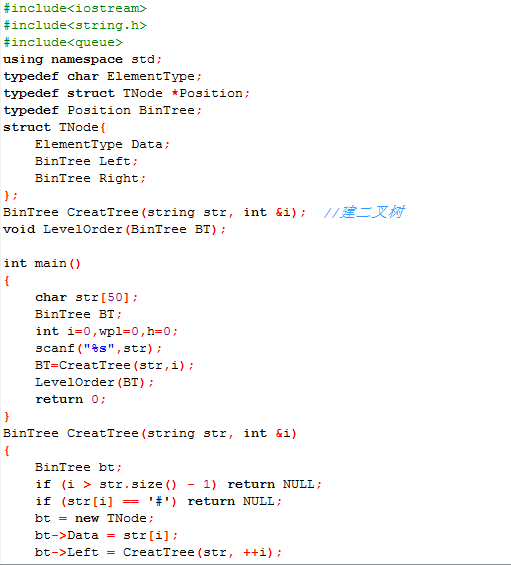


2.3.3本题PTA提交列表说明。

说明:
- bug:应当在对于是否输出完了一层之后再对于curNode进行赋值为队首,否则无法输出第一层的结点
- 总结:之所以把这道题列出来,是觉得这是对于队列的一次很好的练习,在树的遍历来说,相对于其它三种遍历,层次遍历代码量大了一些,更需要细心记住每一部分,要更加仔细编写。
3、阅读代码 
3.1 题目:二叉树剪枝
给定二叉树根结点 root ,此外树的每个结点的值要么是 0,要么是 1,返回移除了所有不包含 1 的子树的原二叉树。( 节点 X 的子树为 X 本身,以及所有 X 的后代。)

3.2 解题思路
- 当我们需要修剪root时,我们需要先修剪root->left、root->right,然后再修剪root。这显然是一个递归定义,所以采用递归法处理。
- 先序遍历会导致某些值为0的节点没被删掉,所以采用后序遍历。
3.3 代码截图
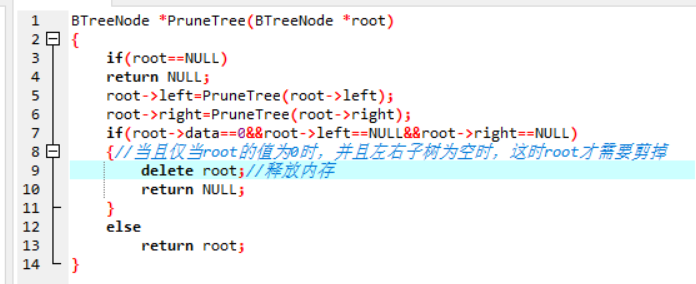
3.4学习体会
- 这道题:递归很巧妙的解决了这个问题,但是很容易卡在用哪种遍历上,起初我以为大概时随便哪种遍历方法都ok,但是后来看见评论才发现先序遍历会删的不彻底,所以以后写题还是要注意细节;
除了这种方法,还可以先利用传递bool标记是否需要修剪,减少剪枝动作。 - 总结:看了一下力扣上有关树的题集,大部分都是采用递归的算法,代码量非常少,看上去感觉特别简单,这道题也是如此,但是递归我觉得算是一个巧思,想到了就很简单,没有的话就还是很难的,而且阅读代码之后的感觉是解题不应该只是完成代码,更关键的是简化代码,会用不同的方法去解题,递归算法需要在更多的练习中去熟练运用。

