BZOJ2087[Poi2010] Sheep

Description

Lyx的QQ牧场养了很多偶数个的羊，他是Vip，所以牧场是凸多边形（畸形）。现在因为他开挂，受到了惩罚，系统要求他把牧场全部分为三角形（划分线不能在牧场中相交，只能在顶点相交），羊也是有个性的，如果他们在三角形中是单数就会有羊自杀（Lyx的样就是畸形），这让Lyx很难办，于是他向你求助了。

Input

输入：第一行由空格隔开的3个整数n（4<=n<=600），k（2<=k<=20000），m(2<=m<=20000)，n表示牧场的顶点数，k表示羊的个数（保证为偶数）。接下来n行为顶点的坐标xi、yi，（-15000<=xi,yi<=15000）由空格隔开，接下来k行为羊的坐标，pi，pj，和xi，yi范围一样但是不会在顶点上，严格在牧场内。

Output

输出：牧场能划分的总方案数被m除的余数。

Sample Input

5 4 10

5 5

3 0

-1 -1

-3 4

1 10

1 0

-1 0

1 6

-2 5

Sample Output

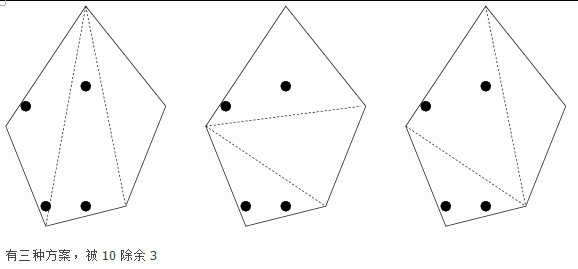
3

Solution

还是被笔者从网上找到题面了啊，虽然并没有BZOJ权限号。。。笔者本想下载题目压缩包然后打开题面，没成想是这个效果：

这个翻译还是没那么明白。。就是把一个n多边形通过连接顶点方式分成\((n-2)\)个三角形， 要求每个三角形里面的点的数量都是偶数。

首先我们可以发现这个多边形的边其实不多，所以我们甚至可以用\(n^3\)的复杂度去解这道题。

然后我们可以自己YY出一个很正确的美妙的定理，就是我们没办法把一个奇数分成两个偶数，这样一来我们的任务就变成了每次都要把它左右的点分成两个都是偶数的部分。然后发现我们可以用极角排序来简化这个过程。然后直接DP就可以了。

用\(f[i][j]\)表示从i顺时针到j之间的已经全部分完了的方案数，可得

\(f[i][j]= \sum_{o=i+1}^{j-1}f[i][o]*f[o][j]\) 。

Code

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <string>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <set>
#include <map>
#define re register
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(arr) memset(arr, 0, sizeof(arr))
const int inf = 0x3f3f3f3f;
struct P
{
	int x,y;
	P(int x=0,int y=0):x(x),y(y){}
	friend P operator -(P x,P y){
		return P(x.x-y.x,x.y-y.y);
	}
	friend double operator *(P x,P y){
		return (x.x*y.y-x.y*y.x);
	} 
};
P a[10001],k[20001],now;
ll m,b[610][610],f[610][610],mo,n;
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();
    while(ch=='-') c*=-1,ch=getchar();
    while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
inline bool cmp(P a,P b)
{
	return (a-now)*(b-now)<0;
}
int main() 
{
    //freopen("date.in","r",stdin);
    n=read();m=read();mo=read();
    for(re int i=1;i<=n;i++)
    	a[i].x=read(),a[i].y=read();
    for(re int i=1;i<=m;i++)
    	k[i].x=read(),k[i].y=read();
    for(re int i=1;i<=n;i++){
    	now=a[i];
    	sort(k+1,k+m+1,cmp);
    	int cnt=0;
    	for(re int j=i+1;j<=n;j++){
    		while(cnt<m&&(k[cnt+1]-now)*(a[j]-now)<0) cnt++;
    		if(cnt&1||(k[cnt+1]-now)*(a[j]-now)==0) continue;
    		b[i][j]=b[j][i]=1;
    	}
    }
    for(re int i=1;i<n;i++)
    	f[i][i+1]=1;
    for(re int l=2;l<n;l++){
    	for(re int L=1;L+l<=n;L++){
    		int R=L+l;
    		if(b[L][R]){
    			for(re int o=L+1;o<R;o++)
    				if(b[L][o]&&b[o][R])
    					f[L][R]+=(f[L][o]*f[o][R])%mo;
    		}
    	}
    }
    cout<<f[1][n]%mo;
    return 0;
}