[CQOI2014]排序机械臂
题目描述
为了把工厂中高低不等的物品按从低到高排好序,工程师发明了一种排序机械臂。它遵循一个简单的排序规则,第一次操作找到高度最低的物品的位置 $P_1$ ,并把左起第一个物品至 $P_1$ 间的物品 (即区间 $[1,P_1]$ 间的物品) 反序;第二次找到第二低的物品的位置 $P_2$ ,并把左起第二个至 $P_2$ 间的物品 (即区间 $[2,P_2]$ 间的物品) 反序……最终所有的物品都会被排好序。
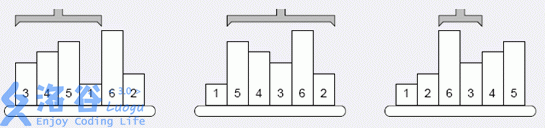
上图给出有六个物品的示例,第一次操作前,高度最低的物品在位置 $4$ ,于是把第一至第四的物品反序;第二次操作前,第二低的物品在位罝六,于是把第二至六的物品反序……
你的任务便是编写一个程序,确定一个操作序列,即每次操作前第 $i$ 低的物品所在位置 $P_i$ ,以便机械臂工作。需要注意的是,如果有高度相同的物品,必须保证排序后它们的相对位置关系与初始时相同。
输入输出格式
输入格式:第一行包含正整数n,表示需要排序的物品数星。
第二行包含n个空格分隔的整数ai,表示每个物品的高度。
输出格式:输出一行包含n个空格分隔的整数Pi。
输入输出样例
说明
N<=100000
Pi<=10^7
首先明白一个事,这个题主体是在让你干什么。这个题明显,要维护一个数据结构,让这个数据结构实现区间翻转和 查询工作。
区间翻转应该都会了吧。不会的请左转去文艺平衡树那个模板题。我这里主要介绍一下建树的操作和查询。
可以发现,那个模板题建树的时候数字是完全有序的,所以可以直接建树。这个题由于给了一个高度,所以不能这么干,然而我们可以使用结构体,以高度为第一关键字,下标为第二关键字sort一下,然后高度就没用了,我们执行模板里的翻转操作即可。
然后我们要求的是什么,一个排名,没错。那么想一下,如果我们把要求的那个点直接旋转到根节点,然后求出它的左子树大小+1是不是就可以了,省去了很多功夫。然而要注意的是,我们因为一开始设置了哨兵节点,所以最后还要-1.
剩下的就没什么很困难的了,不明白的再仔细看看代码吧。
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #include<queue> #define re register #define maxn 1000007 #define ll long long #define ls rt<<1 #define rs rt<<1|1 #define inf 1000000007 using namespace std; int ch[100001][2],f[maxn],cnt[maxn],key[maxn],size[maxn],mark[maxn],root,sz,data[maxn]; struct po { int id,k; }a[maxn]; inline int read() { int x=0,c=1; char ch=' '; while((ch>'9'||ch<'0')&&ch!='-')ch=getchar(); while(ch=='-')c*=-1,ch=getchar(); while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar(); return x*c; } bool cmp(po x,po y) { if(x.k<y.k) return 1; else if(x.k==y.k) return x.id<y.id; return 0; } inline int get(int x) { return ch[f[x]][1]==x; } inline void update(int x) { size[x]=size[ch[x][1]]+size[ch[x][0]]+1; } inline void pushdown(int x) { if(mark[x]){ if(ch[x][0]) mark[ch[x][0]]^=1; if(ch[x][1]) mark[ch[x][1]]^=1; swap(ch[x][0],ch[x][1]); mark[x]=0; } } inline void rotate(int x) { int y=f[x],z=f[y]; int kind=get(x); pushdown(y);pushdown(x); ch[y][kind]=ch[x][kind^1];f[ch[y][kind]]=y; ch[x][kind^1]=y;f[y]=x;f[x]=z; if(z){ ch[z][ch[z][1]==y]=x; } update(y);update(x); } inline void splay(int x,int tar) { for(re int fa;(fa=f[x])!=tar;rotate(x)){ pushdown(f[fa]);pushdown(fa);pushdown(x); if(f[fa]!=tar) rotate(get(x)==get(fa)?fa:x); } if(!tar) root=x; } inline void build(int l,int r,int fa) { if(l>r) return; int mid=l+r>>1; if(mid<fa) ch[fa][0]=mid; else ch[fa][1]=mid; size[mid]=1;f[mid]=fa; if(l==r) return; build(l,mid-1,mid); build(mid+1,r,mid); update(mid); } inline int findx(int x) { int now=root; while(1){ if(mark[now]) pushdown(now); if(x<=size[ch[now][0]]&&ch[now][0]) now=ch[now][0]; else { x-=size[ch[now][0]]+1; if(x==0) return now; else now=ch[now][1]; } } } int main() { int n; cin>>n; for(re int i=2;i<=n+1;i++){ a[i].k=read(); a[i].id=i; } a[1].id=1,a[1].k=-inf; a[n+2].id=n+2,a[n+2].k=inf; sort(a+1,a+n+3,cmp); build(1,n+2,0); root=n+3>>1; for(re int i=2;i<=n;i++){ splay(a[i].id,0); int ans=size[ch[root][0]]+1; printf("%d ",ans-1); int x1=findx(i-1); int y1=findx(ans+1); splay(x1,0);splay(y1,x1); mark[ch[ch[root][1]][0]]^=1; } cout<<n; }

