后缀数组 最详细讲解

转载自后缀数组 学习笔记

后缀数组 最详细(maybe)讲解

后缀数组这个东西真的是神仙操作……

但是这个比较神仙的东西在网上的讲解一般都仅限于思想而不是代码，而且这个东西开一堆数组，很多初学者写代码的时候很容易发生歧义理解，所以这里给出一个比较详细的讲解。笔者自己也是和后缀数组硬刚了一个上午外加一个中午才理解的板子。

本人版权意识薄弱，如有侵权现象请联系博主邮箱xmzl200201@126.com

参考文献：

百度百科_后缀数组

%%%曲神学长的blog%%%

以下是不认识的dalao们：

wsy的cnblog

soda的cnblog

I'MJACKY的cnblog

董雨的cnblog

特别感谢以下的两位dalao，写的特别好，打call

J.K.的cnblog

J_Sure的csdn

什么是后缀数组

我们先看几条定义：

子串

在字符串s中，取任意i<=j，那么在s中截取从i到j的这一段就叫做s的一个子串

后缀

后缀就是从字符串的某个位置i到字符串末尾的子串，我们定义以s的第i个字符为第一个元素的后缀为suff(i)

后缀数组

把s的每个后缀按照字典序排序，

后缀数组sa[i]就表示排名为i的后缀的起始位置的下标

而它的映射数组rk[i]就表示起始位置的下标为i的后缀的排名

简单来说，sa表示排名为i的是啥，rk表示第i个的排名是啥

一定要记牢这些数组的意思，后面看代码的时候如果记不牢的话就绝对看不懂

后缀数组的思想

先说最暴力的情况，快排(n log n)每个后缀，但是这是字符串，所以比较任意两个后缀的复杂度其实是O(n)，这样一来就是接近O(n^2 log n)的复杂度，数据大了肯定是不行的，所以我们这里有两个优化。

ps：本文中的^表示平方而不是异或

倍增

首先读入字符串之后我们现根据单个字符排序，当然也可以理解为先按照每个后缀的第一个字符排序。对于每个字符，我们按照字典序给一个排名(当然可以并列)，这里称作关键字。

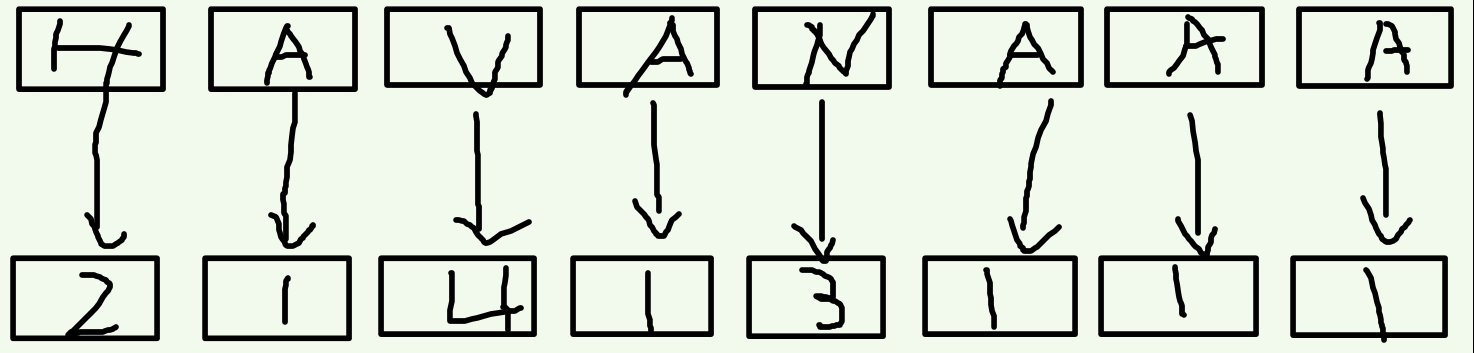
接下来我们再把相邻的两个关键字合并到一起，就相当于根据每一个后缀的前两个字符进行排序。想想看，这样就是以第一个字符(也就是自己本身)的排名为第一关键字，以第二个字符的排名为第二关键字，把组成的新数排完序之后再次标号。没有第二关键字的补零。

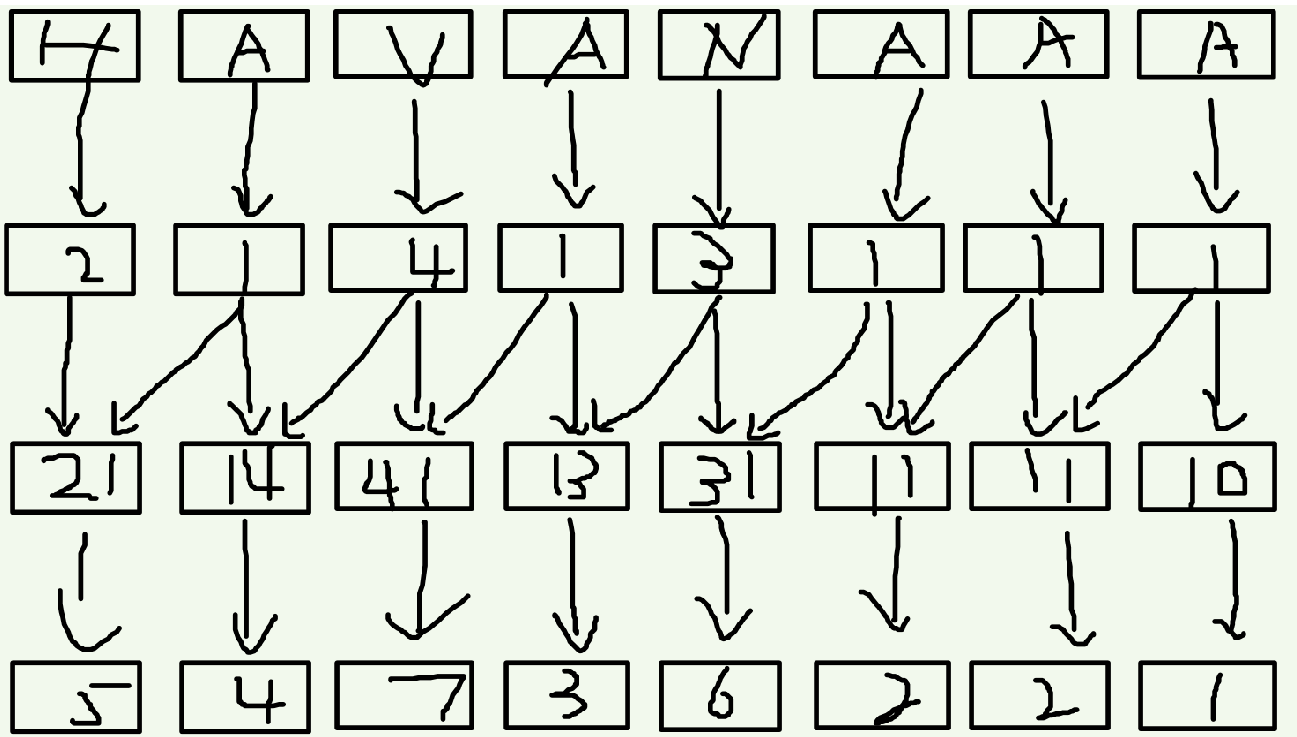
既然是倍增，就要有点倍增的样子。接下来我们对于一个在第i位上的关键字，它的第二关键字就是第(i+2)位置上的，联想一下，因为现在第i位上的关键字是suff(i)的前两个字符的排名，第i+2位置上的关键字是suff(i+2)的前两个字符的排名，这两个一合并，不就是suff(i)的前四个字符的排名吗？方法同上，排序之后重新标号，没有第二关键字的补零。同理我们可以证明，下一次我们要合并的是第i位和第i+4位，以此类推即可……

ps：本文中的“第i位”表示下标而不是排名。排名的话我会说“排名为i”

那么我们什么时候结束呢？很简单，当所有的排名都不同的时候我们直接退出就可以了，因为已经排好了。

显然这样排序的速度稳定在(log n)

基数排序

如果我们用快排的话，复杂度就是(n log^2 n) 还是太大。

这里我们用一波基数排序优化一下。在这里我们可以注意到，每一次排序都是排两位数，所以基数排序可以将它优化到O(n)级别，总复杂度就是(n log n)。

介绍一下什么是基数排序，这里就拿两位数举例

我们要建两个桶，一个装个位，一个装十位，我们先把数加到个位桶里面，再加到十位桶里面，这样就能保证对于每个十位桶，桶内的顺序肯定是按个位升序的，很好理解。

最长公共前缀——后缀数组的辅助工具

话说这个费了我好长时间，就为了证明几条定理……懒得证明的话背过就行了，不过笔者还是觉得知道证明用起来更踏实一些，话说我的证明过程应该比较好懂，适合初学者理解……

什么是LCP？

我们定义LCP(i,j)为suff(sa[i])与suff(sa[j])的最长公共前缀

为什么要求LCP？

后缀数组这个东西，不可能只让你排个序就完事了……大多数情况下我们都需要用到这个辅助工具LCP来做题的

关于LCP的几条性质

显而易见的

1. LCP(i,j)=LCP(j,i);
2. LCP(i,i)=len(sa[i])=n-sa[i]+1;

这两条性质有什么用呢？对于i>j的情况，我们可以把它转化成i<j，对于i==j的情况，我们可以直接算长度，所以我们直接讨论i<j的情况就可以了。

我们每次依次比较字符肯定是不行的，单次复杂度为O(n)，太高了，所以我们要做一定的预处理才行。

LCP Lemma

LCP(i,k)=min(LCP(i,j),LCP(j,k)) 对于任意1<=i<=j<=k<=n

证明：设p=min{LCP(i,j),LCP(j,k)}，则有LCP(i,j)≥p,LCP(j,k)≥p。

设suff(sa[i])=u,suff(sa[j])=v,suff(sa[k])=w;

所以u和v的前p个字符相等，v和w的前p个字符相等

所以u和w的前p的字符相等，LCP(i,k)>=p

设LCP(i,k)=q>p 那么q>=p+1

因为p=min{LCP(i,j),LCP(j,k)}，所以u[p+1]!=v[p+1] 或者 v[p+1]!=w[p+1]

但是u[p+1]=w[p+1] 这不就自相矛盾了吗

所以LCP(i,k)<=p

综上所述LCP(i,k)=p=min{LCP(i,j),LCP(j,k)}

LCP Theorem

LCP(i,k)=min(LCP(j,j-1)) 对于任意1<i<=j<=k<=n

这个结合LCP Lemma就很好理解了

我们可以把i_{k拆成两部分i}(i+1)以及(i+1)~k

那么LCP(i,k)=min(LCP(i,i+1),LCP(i+1,k))

我们可以把(i+1)~k再拆，这样就像一个DP，正确性显然

怎么求LCP？

我们设height[i]为LCP(i,i-1)，1<i<=n，显然height[1]=0;

由LCP Theorem可得，LCP(i,k)=min(height[j]) i+1<=j<=k

那么height怎么求，枚举吗？NONONO，我们要利用这些后缀之间的联系

设h[i]=height[rk[i]]，同样的，height[i]=h[sa[i]];

那么现在来证明最关键的一条定理：

h[i]>=h[i-1]-1;

证明过程来自曲神学长的blog，我做了一点改动方便初学者理解：

首先我们不妨设第i-1个字符串按排名来的前面的那个字符串是第k个字符串，注意k不一定是i-2，因为第k个字符串是按字典序排名来的i-1前面那个，并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。

这时，依据height[]的定义，第k个字符串和第i-1个字符串的公共前缀自然是height[rk[i-1]]，现在先讨论一下第k+1个字符串和第i个字符串的关系。

第一种情况，第k个字符串和第i-1个字符串的首字符不同，那么第k+1个字符串的排名既可能在i的前面，也可能在i的后面，但没有关系，因为height[rk[i-1]]就是0了呀，那么无论height[rk[i]]是多少都会有height[rk[i]]>=height[rk[i-1]]-1，也就是h[i]>=h[i-1]-1。

第二种情况，第k个字符串和第i-1个字符串的首字符相同，那么由于第k+1个字符串就是第k个字符串去掉首字符得到的，第i个字符串也是第i-1个字符串去掉首字符得到的，那么显然第k+1个字符串要排在第i个字符串前面。同时，第k个字符串和第i-1个字符串的最长公共前缀是height[rk[i-1]]，

那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rk[i-1]]-1。

到此为止，第二种情况的证明还没有完，我们可以试想一下，对于比第i个字符串的排名更靠前的那些字符串，谁和第i个字符串的相似度最高（这里说的相似度是指最长公共前缀的长度）？显然是排名紧邻第i个字符串的那个字符串了呀，即sa[rank[i]-1]。但是我们前面求得，有一个排在i前面的字符串k+1，LCP(rk[i],rk[k+1])=height[rk[i-1]]-1;

又因为height[rk[i]]=LCP(i,i-1)>=LCP(i,k+1)

所以height[rk[i]]>=height[rk[i-1]]-1，也即h[i]>=h[i-1]-1。

代码(详细注释)

例题：luogu3809 后缀排序

注意上面那个题不用求lcp……看代码建议先大略扫一遍，因为的确有点绕

#include<iostream>
#include<cstdio>
#include<cstring>
#define rint register int
#define inv inline void
#define ini inline int
#define maxn 1000050
using namespace std;
char s[maxn];
int y[maxn],x[maxn],c[maxn],sa[maxn],rk[maxn],height[maxn],wt[30];
int n,m;
inv putout(int x) {
	if(!x) {
		putchar(48);
		return;
	}
	rint l=0;
	while(x) wt[++l]=x%10,x/=10;
	while(l) putchar(wt[l--]+48);
}
inv get_SA() {
	for (rint i=1; i<=n; ++i) ++c[x[i]=s[i]];
//c数组是桶
//x[i]是第i个元素的第一关键字
	for (rint i=2; i<=m; ++i) c[i]+=c[i-1];
//做c的前缀和，我们就可以得出每个关键字最多是在第几名
	for (rint i=n; i>=1; --i) sa[c[x[i]]--]=i;
	for (rint k=1; k<=n; k<<=1) {
		rint num=0;
		for (rint i=n-k+1; i<=n; ++i) y[++num]=i;
//y[i]表示第二关键字排名为i的数，第一关键字的位置
//第n-k+1到第n位是没有第二关键字的 所以排名在最前面
		for (rint i=1; i<=n; ++i) if (sa[i]>k) y[++num]=sa[i]-k;
//排名为i的数 在数组中是否在第k位以后
//如果满足(sa[i]>k) 那么它可以作为别人的第二关键字，就把它的第一关键字的位置添加进y就行了
//所以i枚举的是第二关键字的排名，第二关键字靠前的先入队
		for (rint i=1; i<=m; ++i) c[i]=0;
//初始化c桶
		for (rint i=1; i<=n; ++i) ++c[x[i]];
//因为上一次循环已经算出了这次的第一关键字 所以直接加就行了
		for (rint i=2; i<=m; ++i) c[i]+=c[i-1]; //第一关键字排名为1~i的数有多少个
		for (rint i=n; i>=1; --i) sa[c[x[y[i]]]--]=y[i],y[i]=0;
//因为y的顺序是按照第二关键字的顺序来排的
//第二关键字靠后的，在同一个第一关键字桶中排名越靠后
//基数排序
		swap(x,y);
//这里不用想太多，因为要生成新的x时要用到旧的，就把旧的复制下来，没别的意思
		x[sa[1]]=1;
		num=1;
		for (rint i=2; i<=n; ++i)
			x[sa[i]]=(y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k]) ? num : ++num;
//因为sa[i]已经排好序了，所以可以按排名枚举，生成下一次的第一关键字
		if (num==n) break;
		m=num;
//这里就不用那个122了，因为都有新的编号了
	}
	for (rint i=1; i<=n; ++i) putout(sa[i]),putchar(' ');
}
inv get_height() {
	rint k=0;
	for (rint i=1; i<=n; ++i) rk[sa[i]]=i;
	for (rint i=1; i<=n; ++i) {
		if (rk[i]==1) continue;//第一名height为0
		if (k) --k;//h[i]>=h[i-1]-1;
		rint j=sa[rk[i]-1];
		while (j+k<=n && i+k<=n && s[i+k]==s[j+k]) ++k;
		height[rk[i]]=k;//h[i]=height[rk[i]];
	}
	putchar(10);
	for (rint i=1; i<=n; ++i) putout(height[i]),putchar(' ');
}
int main() {
	gets(s+1);
	n=strlen(s+1);
	m=122;
//因为这个题不读入n和m所以要自己设
//n表示原字符串长度，m表示字符个数，ascll('z')=122
//我们第一次读入字符直接不用转化，按原来的ascll码来就可以了
//因为转化数字和大小写字母还得分类讨论，怪麻烦的
	get_SA();
//get_height();
}