Machine Learning & Deep Learning Fundamentals

机器学习与深度学习基础

[源自]Reference

---

Deep Learning And Artificial Neural Networks For Beginners

什么是机器学习？

机器学习是一种运用算法分析数据，从数据中学习，并对新数据做出确定和预测的实践。

Machine learning is the practice of using algorithms to analyze data, learn from that data, and then make a determination or prediction about new data.

Deep Learning Explained

什么是深度学习？

深度学习是机器学习的子集，使用的算法受到神经网络的结构和功能的启发。

Deep learning is a sub-field of machine learning that uses algorithms inspired by the structure and function of the brain's neural networks.

深度学习中使用的神经网络与生物神经网络不同，但具有相似的结构，我们称之为人工神经网络（ANNs）

Deep Learning中的Deep是什么意思

1. 首先需要了解ANN的结构
   人工神经网络ANN由神经元组成，神经元构成了ANN中的“层”，除了输入层和输出层的层，称之为隐藏层

2. 如何一个ANN的隐藏层数大于1，则称之为Deep ANN

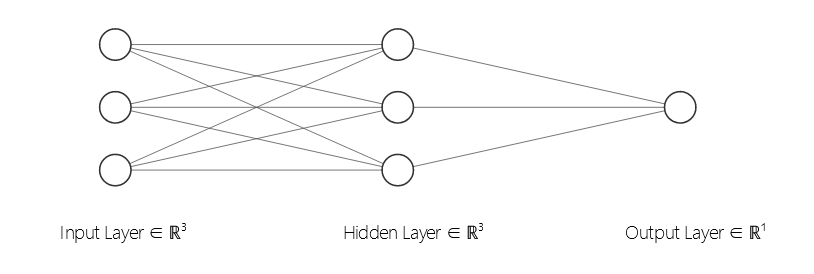
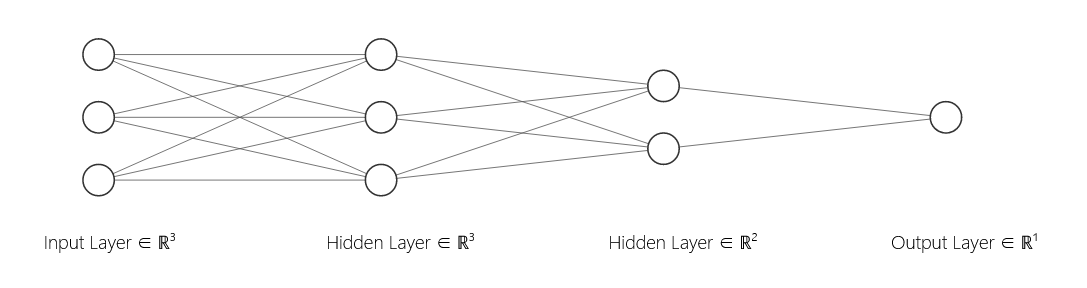
Artificial Neural Networks Explained

图示的ANN，输入层2个神经元（节点），隐藏层3个神经元，输出层2个神经元。所以可以知道该网络的每个输入都必须有两个维度，而每个输入都有两个可能的输出。

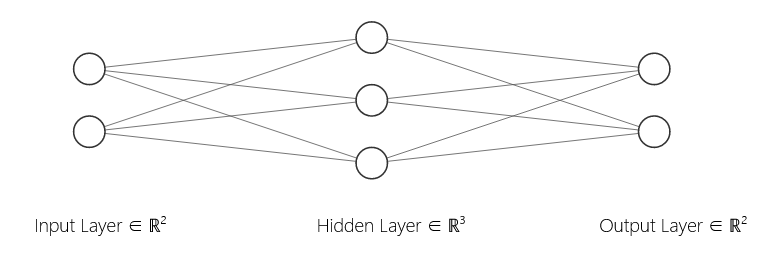
Layers In A Neural Network Explained

神经网络中的层

\(\circ\)密集层（全连接层）
\(\circ\)卷积层
\(\circ\)池化层
\(\circ\)递归层
\(\circ\)规范化层

为什么有不同类型的层

1. 不同的层对它们的输入做不同类型的转换
2. 有的层比其他层更适合做某些工作
     比如卷积层通常用于处理图像数据的模型中；循环层用于处理时间序列数据的模型中；完全连接层将每个输入完全连接到该层的每个输出中。

ANN实例

这个ANN实例中，输入层有８个神经元，其中每个神经元都代表我们数据集中给定样本的一种特征。换句话说，数据集中的一个样本要包含8个维度，当我们将样本传递给模型时，样本包含的八个维度的值都需要提供给输入层相应的神经元。

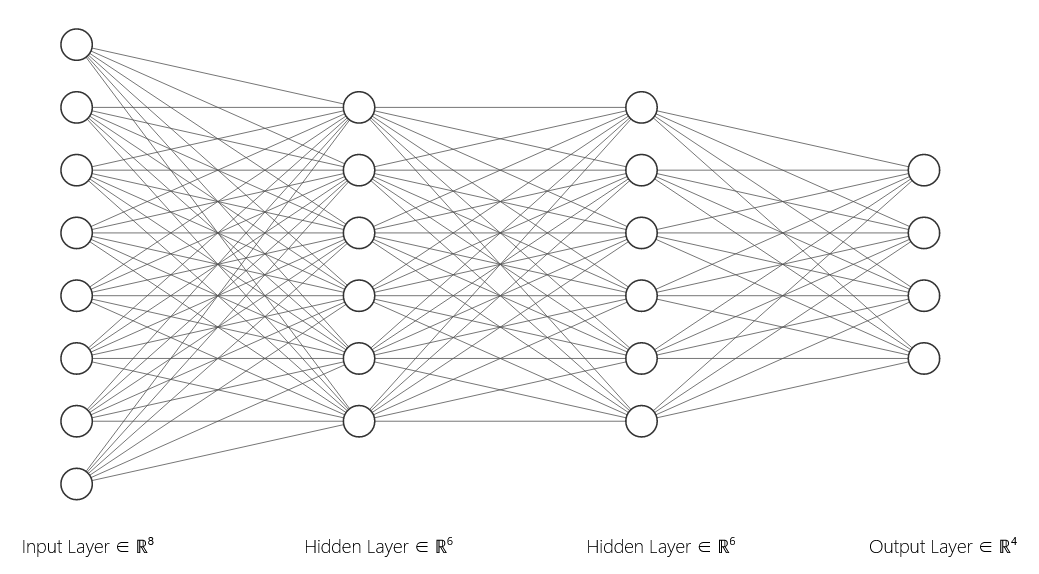
层权重

每两个节点（神经元）之间的连接都是有权重代表它们的关联强度，在输入层给定节点接收到输入时，会将这个输入乘以连接的权重再传递给下一个节点。对于第二层中的节点，还需将加权后的总和传递给激活函数。

\[节点输出=激活函数*(\sum_{n=1}^N 输入*权重) \]

通过神经网络向前传递

获得给定节点的输入后，得到的输出作为下一层的输入，一直持续到输出层。输出层节点数取决于可能的输出或预测类的数量，在这个实例中，我们有四个可能的预测类。假设我们的模型负责对四种类型的动物进行分类。输出层中的每个节点将代表四种可能性之一。例如，我们可以养猫，狗，美洲驼或蜥蜴。

激活函数

激活函数是将节点的输入映射到其相应输出的函数。其将输入的加权总和限定在一个有限的区间内，该函数通常是一个非线性函数。
[为什么使用非线性的激活函数？]
  如果使用线性函数，那么神经网络在前向传递的过程中只进行线性变换，意味着从输入到输出都是线性的，但我们希望我们的神经网络可以计算任意复杂的函数，所以使用非线性的激活函数

Sigmoid激活函数

\[sigmoid(x)=\frac{e^x}{e^{x}+1} \]

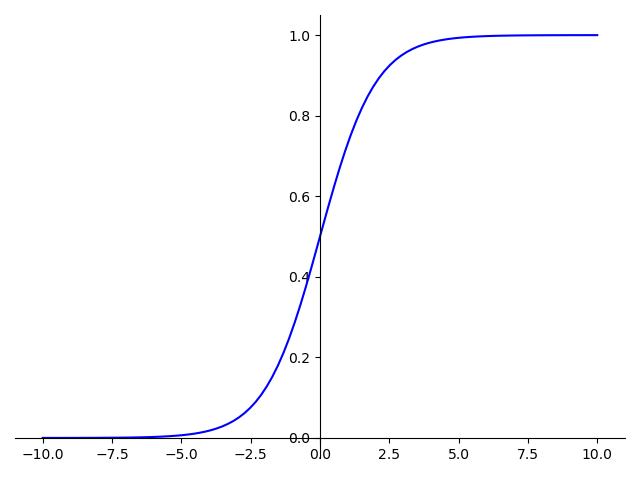
Relu激活函数

\[relu(x)=max(0, x) \]

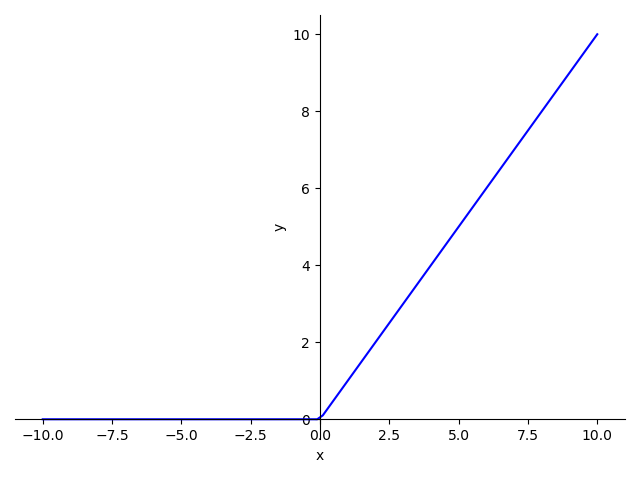
训练ANN

训练模型，实际上就是在尝试解决优化问题（优化模型中的权重），任务是找到最准确的将输出映射到正确类别的权重。训练过程中，权重不断更新朝最佳值移动。

优化算法

通常用优化器optimizer来指代所选的算法，常见的优化器有随机梯度下降SGD。SGD的目标是使损失最小。

损失函数

常见的损失函数有均方差MSE，但是实际损失是什么呢？在训练过程中，我们给模型提供了数据及数据对应的标签。例如，假设我们有一个模型要训练以分类图像是猫还是狗。我们将为模型提供图像，以及这些图像的标签，这些标签说明每个图像是猫还是狗。一张图像经过网络，输出猫的概率和狗的概率。
当所有数据通过模型以后，需将相同的数据重复送进模型中迭代，这就是训练的过程。

ANN的学习方式

当我们的数据集中的所有数据点都通过了网络，说明完成了一次迭代(epoch)
[epoch]
  训练过程中，整个数据集在网络中完成一次传递。

损失函数的梯度

计算出损失以后，根据网络中的每个权重值计算损失的梯度，再根据梯度值来更新模型的权重。梯度会告诉我们哪个方向的损失更小。

学习率

需将梯度值乘以一个学习率。学习率是一个很小的数值，通常在\(0.01\sim 0.0001\)，其实际值是可以变化的。
[学习率]
  是一个超参数，告诉我们应该在去往最小值的方向走多大的一步。过小的学习率会让权重迭代更多的次数才能接近最优解，过大的学习率可能会越过最优解。

更新权值

\[\omega_{new}=\omega_{old}-\alpha*gradient\ \ \ \ \ \ \alpha为学习率 \]

也即

\[\omega=\omega-\alpha*\frac{\partial loss}{\partial \omega} \]

这里我们只拿一个权值来解释概念，实际上，数据通过模型时，每个权值都会发生这样的变化。唯一的区别是，计算损失函数的梯度时，对于每个权值而言梯度的值也会有所不同。所以所有的权值都会在每次epoch中更新，使权值逐渐接近优化值。

模型的学习过程

这种权值的更新过程实际就是模型的学习过程。

损失函数

训练过程中每轮迭代结束的时候，会用输出的预测值与真实值做比较，它们的差值就是损失loss

MSE均方差

对于单个输入\(input\)，预测值\(\hat{y}\)，真实值\(y\)其均方差为

\[MSE(input)=(\hat{y}-y)^{2} \]

如果一次性将整个数据集都传递给模型，那么会在每个epoch结束的时候计算；如果将训练集分成多个批次（batch），一次将一个批次送进模型，那么在每个批次结束时计算损失。

训练集 测试集 验证集

训练集

是用于训练模型的数据集，我们的模型会在训练集中的相同的数据上反复训练，学习数据的特征。这样做的目的是，根据对训练集数据的了解，去预测新数据。

验证集

在训练期间验证我们的模型，验证过程获取的信息可以帮助我们调整超参数。训练期间在每次迭代中，都需要使用训练集对模型进行训练，同时也要使用验证集进行验证。模型会基于对训练集中正在训练的数据的了解，对验证集的输入进行分类。
[注意]
  模型不会根据我们在验证集得到的损失去更新权重。

训练集和验证集的数据是分开的，所以验证的数据不包含模型已经从训练集中熟悉的样本。

需要验证集的原因

确保模型不会过拟合（过拟合的模型无法对未经训练的数据进行准确分类）。如果在训练集中可以得到很好的分类结果，但是验证集的结果不好，就说明我们的模型过拟合了。
  验证集使我们可以看到模型在训练过程中的推广程度。

测试集

测试集与其他两个数据集的区别是没有标签，用于最终的泛化能力检查。

如何避免过拟合

[过拟合]
  模型可以对训练集准确分类，但验证和测试时效果不好

在训练集中加入更多的数据

数据扩增 Data Augmentation

通过合理修改训练集中的数据来创建额外的扩增数据的过程。对与图像数据而言，可能的修改方法有：裁剪、旋转、缩放等

降低模型的复杂性

1. 从模型中删除某些层
2. 降低层中神经元的个数

随机失活（dropout）

在学习过程中通过将隐含层的部分权重或输出随机归零，降低节点间的相互依赖性（co-dependence ）从而实现神经网络的正则化（regularization），降低其结构风险

如何避免欠拟合

[欠拟合]
  模型无法对所训练的数据进行分类。

增加模型复杂性

1. 增加层数
2. 增加层中神经元个数

在输入样本中加入更多特征

减少dropout

监督学习

监督学习需要给模型提供标签，其训练数据都是成对的，有输入-输出，或样本-标签。

无监督学习

训练集的数据是没有标签的，模型将尝试从数据中学习某种类型的结构并提取有用的信息或特征

聚类算法

自动编码器

假设有一组手写数字图像，并将它们传递给自动编码器（是一个神经网络），该神经网络将获取该数字图像，然后对其进行编码，在网络的末端，它将解码图像并输出原始图像的解码后的重建版本。这里的目标是使重建图像尽可能接近原始图像
在不目视检查原始图像的情况下，我们如何测量这种自动编码器的性能呢？我们可以将这种自动编码器的损失函数视为测量图像的重建版本与原始版本的相似程度。重建图像与原始图像越相似，损失越小。

半监督学习

半监督学习采用一种有监督和无监督结合的方式，我们既有“有标签的数据”又有“无标签的数据”时，会采用半监督学习的方法。在半监督学习中，将使用伪标签。

伪标签 Pseudo-Labeling

首先需要标记数据集中的一部分数据，然后利用这些有标签的数据训练模型。训练完成后，使用模型对未标记的数据进行预测，用我们预测得到的每个输出为它们标记。伪标记使我们可以在更大的数据集上进行训练。
[伪标签的本质]
  用模型预测的输出去为未标记的数据添加标签

独热编码

模型预测的输出不会是各个单词，而是0（冷值），1（热值）组成的向量，向量中有一个指标是热值。向量的维度和我们需要分类的类别数有关。比如分成猫、狗、蜥蜴，则有如下向量

标签	向量
猫	[1,0,0]
狗	[0,1,0]
蜥蜴	[0,0,1]

若分成四类，如猫、狗、蜥蜴、骆驼，则有

标签	向量
猫	[1,0,0,0]
狗	[0,1,0,0]
蜥蜴	[0,0,1,0]
骆驼	[0,0,0,1]

卷积神经网络 CNN

卷积神经网络可以识别或检测模式，所以CNN对图像分析很有用。
CNN具有卷积层

卷积层

卷积层的输入成为输入通道，输出成为输出通道。卷积层中的转换属于卷积运算，在数学上，这样的卷积运算实际上称为互相关

滤波器和卷积运算

对于每个卷积层，我们需要指定滤波器的数目，这些滤波器用于检测模式。比如单个图像可能有一下模式：边缘、形状、纹理、曲线、颜色等，如果某个滤波器可以检测到图像的边缘，可以称之为边缘检测器。网络越深入，滤波器就会越复杂，因此在更深的层中，滤波器可以检测出更复杂的物体。

滤波器的数目决定输出通道的数目
从技术上讲，滤波器相当于一个相对较小的矩阵（张量），我们需要确定矩阵的行数和列数，并用随机数进行初始化。

卷积操作示例

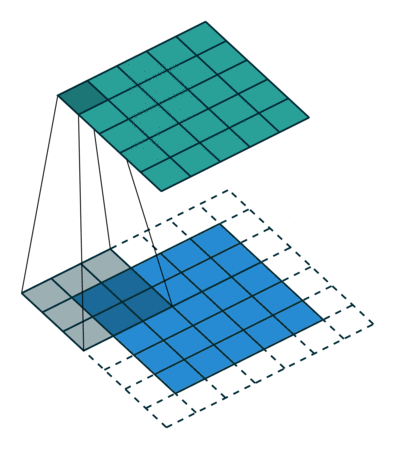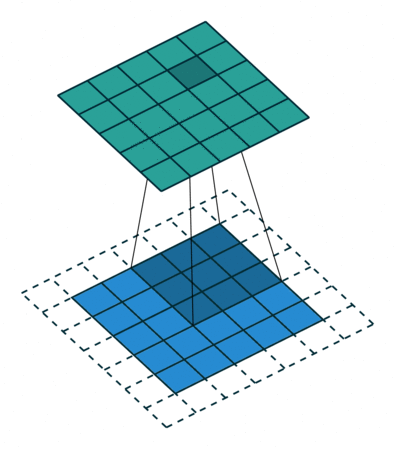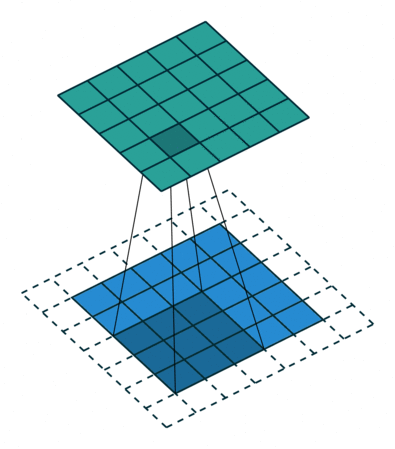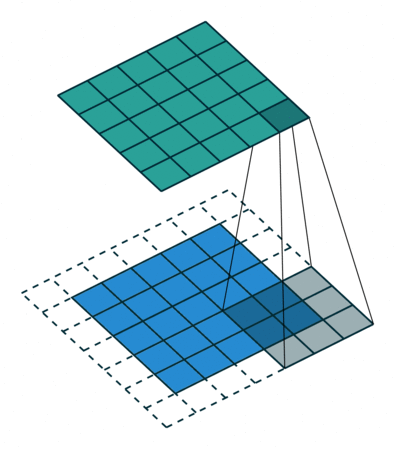
比如，我们指定第一个卷积层包含一个大小为\(3\times3\)的滤波器。下图的动画中，包含：
\(\circ\)输入通道（底部/蓝色）
\(\circ\)\(3\times3\)卷积滤波器（底部阴影）
\(\circ\)输出通道（顶部/绿色）

输入通道的每个位置，滤波器都会进行计算，并将它们映射到输出通道（对应的阴影部分）。该卷积层接受一个输入通道后，滤波器会以$3\times3$的像素块为单位在输入通道滑动，直到滑过整个图像所有$3\times3$的像素块。这种**滑动**就是**卷积**。 蓝色的输入通道是来自MNIST数据集的图像的矩阵表示。此矩阵中的值是图像中的单个像素，这些图像是灰度图像，因此我们只有一个输入通道。

\(\circ\)灰度图像只有一个颜色通道
\(\circ\)RGB图像有三个颜色通道
输入将被传递到卷积层。前面有提到，我们指定第一个卷积层只有一个滤波器，这个滤波器将会卷积输入的每一个像素块。当滤波器落在第一个像素块时，将计算并存储滤波器本身与像素块的点积。当滤波器对整个输入做完卷积后得到的输出通道，将会作为下一层的输入通到。

输入和输出通道

假设用MNIST数据集中7的灰度图像作为我们的输入。

设第一个卷积层中有4个滤波器，滤波器的值如下，其中-1代表黑色，1代表白色，0代表灰色。

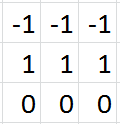
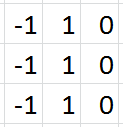
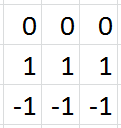
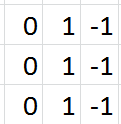
如果用这四个滤波器分别对原始的7的图像做卷积处理，各滤波器的输出通道如下图所示：

可以看到四个滤波器都在检测边缘，再输出通道中，最亮的像素可以被解释为滤波器检测到的像素。在第一个输出中，我们可以看到检测出7的顶部水平边缘，这部分最亮（白色）；第二个检测左侧垂直边缘； 第三个检测底部水平边缘；第四个检测右侧垂直边缘。 这些滤波器仅能检测边缘，它们位于卷积神经网络的开始，更复杂的滤波器位于网络的更深处，可以检测出更复杂的模式。 令人惊奇的是，模式检测器是由网络自动派生的。滤波器的值以随机值开始，并且随着网络在训练期间学习而改变，其模式检测功能会自动出现。