04 Back Propagation
Compute Gradient in complicated network
- 在简单的网络中计算梯度
- 最简单的线性模型可能是\(\hat{y}=x*\omega+b\),在两层网络中,\(\hat{y}=W_2(W_1*x+b_1)+b_2\),如果不做其他处理,实际上又可以整理成
\[\hat{y}=W_{1}W_{2}*x+W_{2}b_{1}b_{2}
\]
\[=W*x+b
\]
这样的话,不管有多少层网络,它的实际效果和一层是一样的,因此,在每层计算出结果后还需要再经过一个非线性函数(激励函数\(\sigma\)),再将激励函数的结果作为下一层的输入。
3. BP基本过程
import torch
import matplotlib.pyplot as plt
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w = torch.Tensor([1.0])
w.requires_grad = True
def forward(x):
return x*w
def loss(x,y):
y_pred = forward(x)
return (y_pred-y)**2
print("Predict (before training): ", 4, forward(4).item())
l = 0
l_list = []
epoch_list = []
cnt = 0
for epoch in range(100):
for x,y in zip(x_data,y_data):
l = loss(x,y)
l.backward()
print('\tgrad:',x,y,w.grad.item())
w.data = w.data - 0.01*w.grad.data
w.grad.data.zero_()
l_list.append(l.item())
epoch_list.append(epoch)
print("Process: ", epoch, l.item())
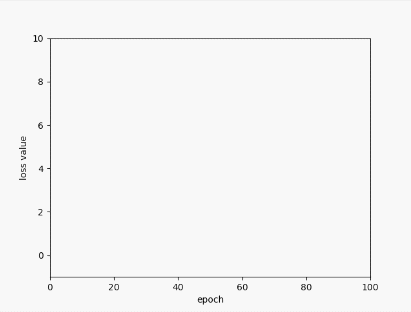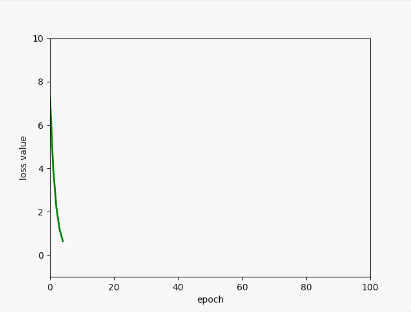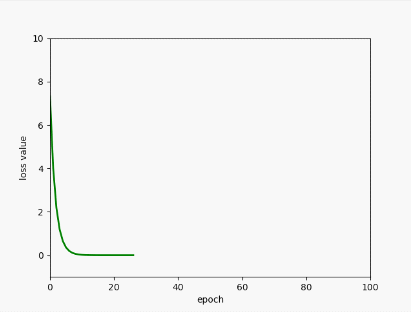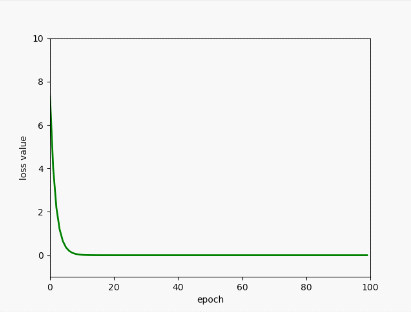
plt.plot(epoch_list, l_list, color="green", linewidth=2)
plt.xlabel("epoch")
plt.ylabel("loss value")
plt.xlim(0, 100)
plt.ylim(-1, 10)
plt.savefig("E:\\Result\\lecture04BP\\{0}.png".format(cnt))
plt.show()
cnt += 1
print("Predict (after training): ", 4, forward(4).item())