03 Gradient Descent

Linear Model

1. 假设已有数据x_data = [1.0, 2.0, 3.0]，y_data = [2.0, 4.0, 6.0]
2. 线性模型为

\[\hat{y}=x*\omega \]

3. 损失函数（均方差MSE）为：

\[cost(\omega)=\frac{1}{N}\sum_{n=1}^N(\hat{y_n}-y_n)^{2} \]

Gradient Descent Algorithm

1. 我们给定一个初始的\(\omega\)值，梯度gradient为：

\[\frac{\partial cost}{\partial \omega} \]

2. 整理梯度公式有：

\[\frac{\partial cost}{\partial \omega}=\frac{\partial}{\partial \omega}\frac{1}{N}\sum_{n=1}^N(x_n*\omega-y_n)^2 \]

\[=\frac{1}{N}\sum_{n=1}^N\frac{\partial}{\partial \omega}(x_n*\omega-y_n)^2 \]

\[=\frac{1}{N}\sum_{n=1}^N 2*x_n(x_n*\omega-y_n) \]

至此，求梯度值的函数gradient即可写出。
3. 我们希望梯度越来越小，同时也不想权值\(\omega\)跳得太快，所以会有：

\[\omega=\omega-\alpha*gradient \]

来更新\(\omega\)，这里的\(\alpha\)是学习率，这是一个人为设定的正数。（过小的学习率会让\(\omega\)迭代更多的次数才能接近最优解，过大的学习率可能会越过最优解并逐渐发散）
4. 本次实验迭代了100次，迭代的大致过程如下

import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

def forward(x):
    return x * w

def cost(xs, ys):
    result = 0
    for x,y in zip(xs, ys):
        y_pred = forward(x)
        result += (y_pred - y) ** 2
    return result / len(xs)

def gradient(xs, ys):
    grad = 0
    for x,y in zip(xs, ys):
        grad += 2 * x * (x * w - y)
    return grad / len(xs)

print('Predict (before training)', 4, forward(4))

cost_list = []
epoch_list = []

for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data,y_data)
    w -= 0.01*grad_val
    print('Epoch:', epoch, 'w=', w, 'loss=', cost_val)

    cost_list.append(cost_val)
    epoch_list.append(epoch)
    plt.plot(epoch_list, cost_list)
    plt.xlabel('epoch')
    plt.ylabel('cost value')
    plt.show()

print('predict (after training)', 4, forward(4))

Stochastic Gradient Descent(SGD)

随机梯度下降法
如果使用梯度下降法，每次⾃自变量量迭代的计算开销为 ，它随着 线性增⻓长。因此，当训练数据样本数很⼤大时，梯度下降每次迭代的计算开销很高。SGD减少了每次迭代的开销，在每次迭代中只随机采一个样本并计算梯度。

	梯度下降法	随机梯度下降法
\(\omega\)	\(\omega=\omega-\alpha\frac{\partial cost}{\partial \omega}\)	\(\omega=\omega-\alpha\frac{\partial loss}{\partial \omega}\)
损失函数导函数	\(\frac{\partial cost}{\partial \omega}=\frac{1}{N}\sum_{n-1}^N2 x_n (x_n \omega - y_n)\)	\(\frac{\partial loss_n}{\partial \omega}=2 x_n (x_n \omega - y_n)\)

# -*- coding: utf-8 -*-
"""
Created on Wed Aug 26 11:01:09 2020

@author: huxu
"""

import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

def forward(x):
    return x*w

def loss(x,y):
    y_pred = forward(x)
    return (y_pred-y)**2

def gradient(x, y):
    return 2*x*(x*w-y)

print('Predict (before training)', 4, forward(4))

loss_list = []
epoch_list = []

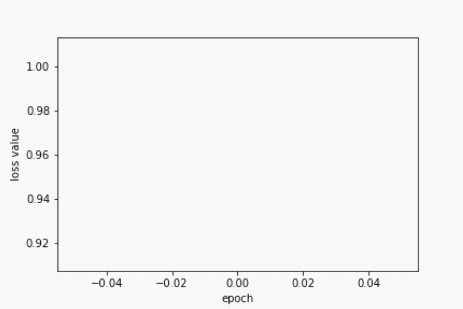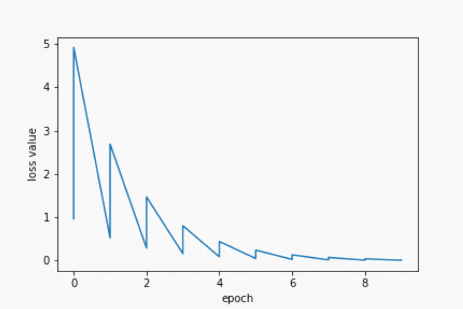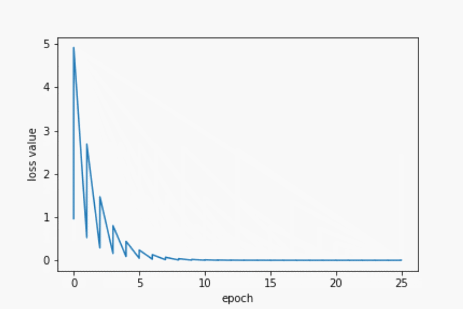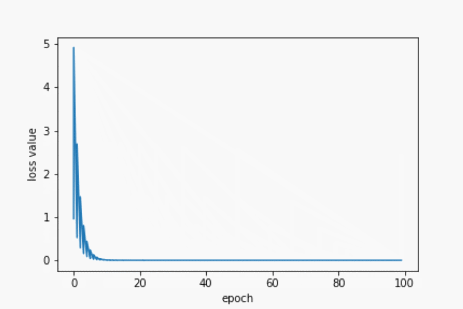
for epoch in range(100):
    for x,y in zip(x_data, y_data):
        grad = gradient(x, y)
        w -= 0.01 * grad
        print('\tgrad: ',x,y,grad)
        l = loss(x,y)
    
        loss_list.append(l)
        epoch_list.append(epoch)
        plt.plot(epoch_list, loss_list)
        plt.xlabel('epoch')
        plt.ylabel('loss value')
        plt.show()
        
    print("process: ",epoch,"w= ",w,"loss=",l)

print('predict (after training)', 4, forward(4))

Reference

[1] https://www.bilibili.com/video/BV1Y7411d7Ys?p=3
[2] Dive-into-DL-PyTorch