02 Linear Model

Linear Model

1. 假设已有数据x=[1.0, 2.0, 3.0]，y=[5.0, 8.0, 11.0]，如图：
   
2. 线性模型为\(\hat{y}=x*\omega+b\)
3. 损失函数为\(loss=(\hat{y}-y)^{2}\)
4. 设定w,b我们认为比较合适的取值范围

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm

x_data = [1.0, 2.0, 3.0]
y_data = [5.0, 8.0, 11.0]

def forward(x):
    return x * w + b

def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

w = np.arange(0.0, 5.1, 0.1)
b = np.arange(0.0, 5.1, 0.1)

w,b = np.meshgrid(w,b)

x_data = np.array(x_data)
y_data = np.array(y_data)

loss_sum = 0
for i in range(3):
    loss_sum += ((w * x_data[i] + b) - y_data[i]) ** 2
mse = loss_sum/3
print(mse)

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
surf = ax.plot_surface(w,b,mse,cmap=cm.coolwarm)
ax.set_xlabel(r'$\omega$')
ax.set_ylabel(r'$b$')
ax.set_zlabel(r'$mse$')

ax.view_init(elev=10,
             azim=-50)
plt.show()

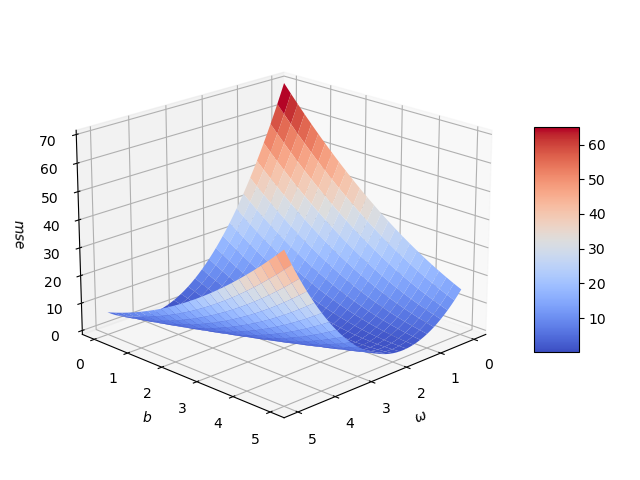
5. 结果
   
   

Reference

[1] https://www.bilibili.com/video/BV1Y7411d7Ys?p=2
[2] https://matplotlib.org/gallery/mplot3d/surface3d.html
[3] https://www.cnblogs.com/shanger/p/13199228.html