蒙特卡洛方法

蒙特卡洛方法（Monte Carlo method），也称统计模拟方法，它是一种思想或者方法的统称，而不是严格意义上的算法。

蒙特卡洛方法的起源是1777年由法国数学家布丰（Comte de Buffon）提出的用投针实验方法求圆周率（具体算法见文末的好文推荐），在20世纪40年代中期，由于计算机的发明结合概率统计理论的指导，从而正式总结为一种数值计算方法，其主要是用随机数来估算计算问题。

基本思想

为了求解问题，首先建立一个概率模型或随机过程，使它的参数或数字特征等于问题的解，然后通过对模型或过程的观察或抽样试验来计算这些参数或数字特征，最后给出所求解的近似值 —— 解的精确度用估计值的标准误差来表示。

• 主要理论基础：概率统计中的大数定律。
• 主要手段：随机抽样、统计试验。

用蒙特卡洛方法求解实际问题的基本步骤为：

• 根据实际问题的特点．构造简单而又便于实现的概率统计模型．使所求的解恰好是所求问题的概率分布或数学期望；
• 给出模型中各种不同分布随机变量的抽样方法；
• 统计处理模拟结果，给出问题解的统计估计值和精度估计值。

方法举例 [Python]

求圆周率PI：

import random
import math
import sys
import matplotlib.pyplot as plt


def test_monte_carlo():
    n = 0

    # Repeat try the estimate pi, until break it down manually
    while True:
        print('Start experiment: ')
        total = 0
        n = int(input(sys.argv))

        for i in range(n):
            x = random.uniform(-1, 1)
            y = random.uniform(-1, 1)

            # x^2 + y^2 <=1, means (x, y) in the cycle
            if math.sqrt(x ** 2 + y ** 2) <= 1.0:
                total += 1
                plt.plot(x, y, 'ro')
            # x^2 + y^2 > 1, means (x, y) out of the cycle
            else:
                plt.plot(x, y, 'b*')

        # r = n / 2
        mypi = 4.0 * total / n

        # plot the x, y and close it after 5 seconds
        plt.ion()
        plt.pause(5)
        plt.close()

        print('Iteration Times = ', n, 'PI estimate value = ', mypi)
        print('math.pi = ', math.pi)
        print('Errors = ', str(abs(math.pi - mypi) / math.pi * 100)[:5]+'%')
        # print('Errors = ', abs(math.pi - mypi) / math.pi)

当输入的n=100时：PIestimate= 3.2，Errors= 0.0186。

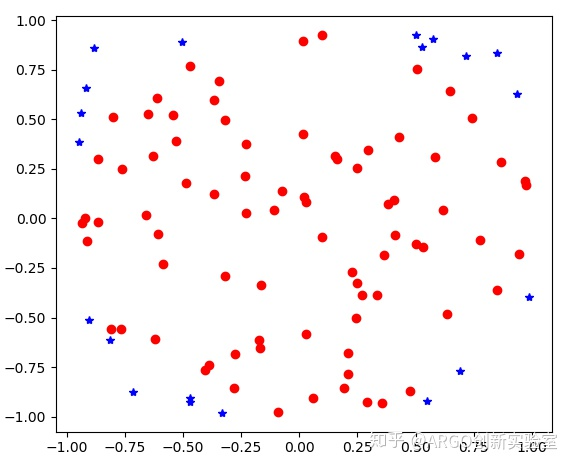
当输入的n=1000时：PIestimate= 3.448，Errors= 0.0975。

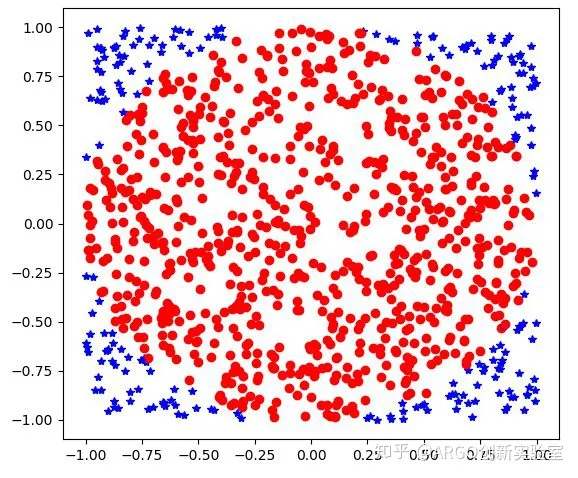
由上述结果貌似会误导读者得到一个点越多反而估算越不准确的结论，这正是希望大家不要想当然的认为点越多越精确的直觉影响。但是，一般当数量达到某个量级之后，蒙特卡罗算法的特点是，采样越多，越近似最优解，而永远不是最优解。

参考

1. 百度百科：蒙特卡罗法
2. 知乎专栏：蒙特卡罗算法