贪心算法实例（四）求解单源最短路径问题（Bellman-Ford算法）

问题

给定带权有向图G =(V,E)，其中每条边的权是非负实数。另外，还给定V中的一个顶点，称为源。现在要计算从源到所有其他各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。

例如，Patrick教授希望找到一条从菲尼克斯(Phoenix)到印第安纳波利斯(Indianapolis)的最短路径。给定一幅美国的道路交通图，上面标有所有相邻城市之间的距离，Patrick教授怎样才能找出这样一条最短的路径呢？一种可能的办法当然是，先将从菲尼克斯到印第安纳波利斯的所有路径都找出来，将每条路径上的距离累加起来，然后选择其中最短的路径。但是，即使在不允许环路的情况下，也可以看得出来，Patrick教授需要检查无数种可能的路径，而其中的大多数路径根本不值得检查 —— 一条从菲尼克斯经过西雅图再到印第安纳波利斯的路径显然不符合要求，因为西雅图已经偏离了目标方向好几百英里。

思路

Bellman-Ford算法

Bellman-Ford算法解决的是一般情况下的单源最短路径问题，在这里，边的权重可以为负值。给定带权重的有向图G=(V, E)和权重函数w: E→R，Bellman-Ford算法返回一个布尔值，以表明是否存在一个从源节点可以到达的权重为负值的环路，如果存在这样一个环路，算法将告诉我们不存在解决方案，如果没有这种环路存在，算法将给出最短路径和它们的权重。

权重为负值的环路：如果有这样的环路，最短路径会出现错误的循环，所以导致输出不正确。

 

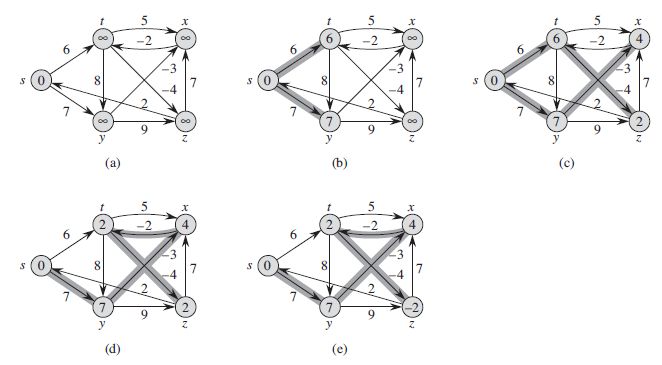
1. 从源结点为s，给剩余其他结点路径距离赋值为无穷大。（图a）
2. 访问每条边，进行松弛操作，更新节点距离。（图b到图e）
3. 检查图中是否存在权重为负值的环路并返回与之适应的布尔值。

伪代码

 

实现

# Python 3: Bellman Ford Algorithmclass Vertex(object):
    def __init__(self, name: str, value: int = -1):
        self.name: str = name
        self.value: int = value
        self.dist = float('Inf')  # shortest distance from source vertex.
        self.prev = None  # previous vertex with shortest distance


class Edge(object):
    def __init__(self, start: Vertex, end: Vertex, weight: int):
        self.start: Vertex = start
        self.end: Vertex = end
        self.weight: int = weight


class Graph:
    def __init__(self, V, E):
        """

        :param V: a collection of vertex
        :param E: a collection of edges
        """
        self.V = V
        self.E = E


def bellman_ford(G: Graph, s: int):
    G = initialize_single_source(G, s)
    for i in range(1, len(G.V)):
        for e in G.E:
            e.end = relax(e.start, e.end, e.weight)
    for e in G.E:
        if e.end.dist > e.start.dist + e.weight:
            return False
    return True


def initialize_single_source(G, s: int):
    """

    :param G:
    :param s: source vertex
    """
    for v in G.V:
        v.dist = float('Inf')
        v.prev = None
    G.V[s].dist = 0
    return G


def relax(u, v, w):
    """

    :param u: previous (possibly) vertex u
    :param v: current vertex v
    :param w: weight of edge from vertex u to vertex v.
    :return:
    """
    if v.dist > u.dist + w:
        v.dist = u.dist + w
        v.prev = u
    return v


#s = Vertex('s', -1)
#t = Vertex('t', -1)
#y = Vertex('y', -1)
#x = Vertex('x', -1)
#z = Vertex('z', -1)
#V = [s, t, y, x, z]

#E = [
#    Edge(s, t, 6),
#    Edge(s, y, 7),
#    Edge(t, y, 8),
#    Edge(t, x, 5),
#    Edge(t, z, -4),
#    Edge(y, x, -3),
#    Edge(y, z, 9),
#    Edge(x, t, -2),
#    Edge(z, s, 2),
#    Edge(z, x, 7),
#]
#
#G = Graph(V, E)
#
#print(bellman_ford(G, 0))
#for v in G.V:
#    print(f'vertex {v.name} dist: {v.dist}')
#
#-----
#True
#vertex s dist: 0
#vertex t dist: 2
#vertex y dist: 7
#vertex x dist: 4
#vertex z dist: -2

参考

• Bellman-ford算法详解——负权环分析_anlian523的博客-CSDN博客_bellman-ford