动态规划实例(四)最优二叉搜索树(Optimal Binary Search Tree)
问题
最优二叉搜索树(Optimal Binary Search Tree,Optimal BST)问题,形式化定义:给定一个n个不同关键字的已排序的序列K=<k1, k2, ..., kn>(k1<k2<...<kn),用这些关键字构造一棵二叉搜索树 —— 对每个关键字ki,都有一个概率pi表示其搜索频率。对于不在K中的搜索值构造n+1个”伪关键字“d0, d1, d2, ..., dn —— 伪关键字di表示所有在ki和ki+1之间的值(i=1,2,...,n-1,d0表示所有小于k1的值,dn表示所有大于kn的值),每个伪关键字di对应一个概率qi(搜索频率)。
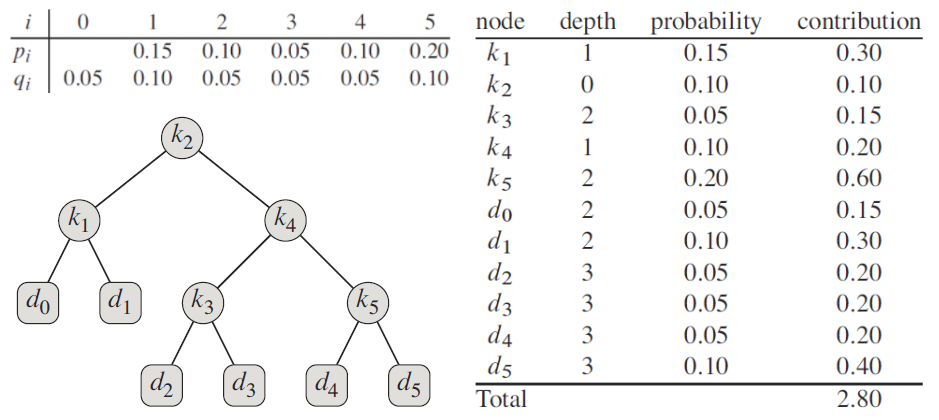
例如,对一个n=5的关键字集合及如下的搜索频率,构造二叉搜索树。逐点计算的期望搜索耗费(contribution = (depth + 1) * probability)如右下表,从表中得到k5的搜索概率最高,根节点是k2。
二叉树搜索树的期望耗费:
思路
- 步骤1:最优二叉搜索树的结构,如果一颗最优二叉搜索树T有一颗包含关键字ki, ..., kj的子树T',那么T'必然是包含ki, ..., kj和伪关键字di-1, ..., dj的子问题最优解。
- 步骤2:一个递归式,定义w(i, j)是包含关键字ki, ..., kj的子树所有概率之和,e[i, j]为期望耗费,则...
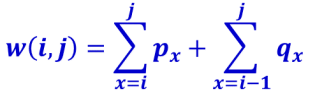
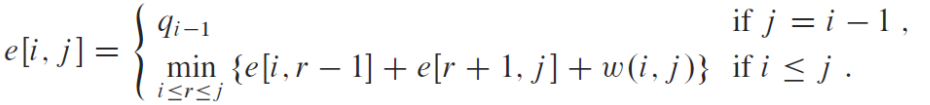
- 步骤3:计算最优二叉搜索树的期望代价。
实现
def optimal_bst(p,q,n): e=[[0 for j in range(n+1)]for i in range(n+2)] w=[[0 for j in range(n+1)]for i in range(n+2)] root=[[0 for j in range(n+1)]for i in range(n+1)] for i in range(n+2): e[i][i-1]=q[i-1] w[i][i-1]=q[i-1] for l in range(1,n+1): for i in range(1,n-l+2): j=i+l-1 e[i][j]=float("inf") w[i][j]=w[i][j-1]+p[j]+q[j] for r in range(i,j+1): t=e[i][r-1]+e[r+1][j]+w[i][j] if t<e[i][j]: e[i][j]=t root[i][j]=r return e,root if __name__=="__main__": p=[0,0.15,0.1,0.05,0.1,0.2] q=[0.05,0.1,0.05,0.05,0.05,0.1] e,root=optimal_bst(p,q,5) for i in range(5+2): for j in range(5+1): print(e[i][j]," ",end='') print() for i in range(5+1): for j in range(5+1): print(root[i][j]," ",end='') print()
时间复杂度:T(n)=O(n3)
空间复杂度:S(n)=O(n2)
代码引自:算法导论程序39--最优二叉搜索树(Python)_夜空霓虹的博客-CSDN博客_最优二叉搜索树python


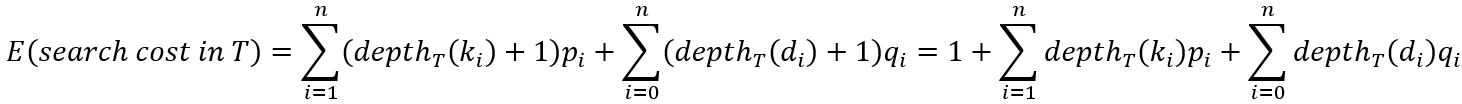

 浙公网安备 33010602011771号
浙公网安备 33010602011771号