动态规划实例（三）求解最长公共子序列问题

问题

最长公共子序列问题（longest-common-subsequnence problem, LCS），给定两个序列X=<x₁, x₂, ..., x_m>, Y=<y₁, y₂, ..., y_n>，求X和Y长度最长的公共子序列。

例如，<B, C, B, A>就是X=<A, B, C, B, D, A, B>, Y=<B, D, C, A, B, A>的公共子序列。

思路

暴力法

穷举X的所有子序列，对每个子序列检查它是否也是Y的子序列，记录找到的最长子序列。因为X的每个子序列对应X的下标集合是{1, 2, ..., m}的一个子集，所以X有2^m个子序列，因此，暴力法的运行时间是指数阶的。

动态规划

• 步骤1：刻画最长公共子序列的特征 —— 令Z=<z₁, z₂, ..., z_k>是X和Y的LCS，那么
  • 若x_m=y_n，则z_k=x_m=y_n，且Z_k-1是X_m-1和Y_n-1的一个LCS。
  • 若x_m≠y_n，则z_k≠x_m，则Z是X_m-1和Y的一个LCS。
  • 若x_m≠y_n，则z_k≠y_m，则Z是X和Y_n-1的一个LCS。
• 步骤2：一个递归解 —— 根据步骤1，可以得到如下公式：

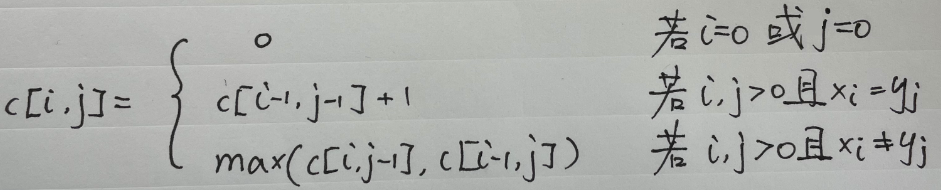
• 步骤3：计算LCS长度 —— 根据步骤2，我们可以写出一个指数时间的递归算法来计算两个序列的LCS长度，但是LCS问题只有O(mn)个不同的子问题，我们可以用动态规划方法自底向上地计算。

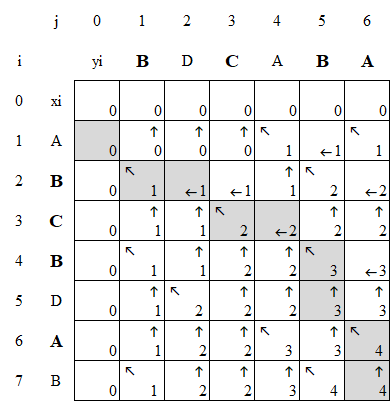
• 步骤4：构造LCS的解。 

Python 3实现

动态规划

import numpy as np


def LCS(X, Y):
    c, b = LCS_length(X, Y)
    print(c)
    print(b)
    print_LCS(b, X, len(X), len(Y))


def LCS_length(X, Y):
    m = len(X)
    n = len(Y)
    b = np.zeros((m , n), dtype=np.int)
    c = np.zeros((m + 1, n + 1), dtype=np.int)

    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if X[i - 1] == Y[j - 1]:
                c[i, j] = c[i - 1, j - 1] + 1
                b[i - 1, j - 1] = 2  # 斜上箭头
            elif c[i - 1, j] >= c[i, j - 1]:
                c[i, j] = c[i - 1, j]
                b[i - 1, j - 1] = 0  # 向上箭头
            else:
                c[i, j] = c[i, j - 1]
                b[i - 1, j - 1] = 1  # 向左箭头
    return c, b


def print_LCS(b, X, i, j):
    if i == 0 or j == 0:
        return
    if b[i-1, j-1] == 2:  # 斜上箭头
        print_LCS(b, X, i - 1, j - 1)
        print(X[i-1])
    elif b[i-1, j-1] == 0:  # 向上箭头
        print_LCS(b, X, i - 1, j)
    else:
        print_LCS(b, X, i, j - 1)