动态规划实例（一）求解钢条切割问题

问题

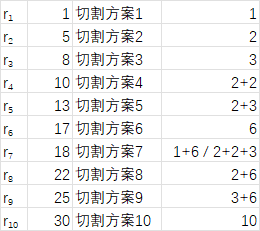
Serling公司购买长钢条，将其切割为短钢条出售。切割工序本身没有成本支出。公司管理层希望知道最佳的切割方案。假定我们知道Serling公司出售一段长为i英寸的钢条的价格为p_i(i=1,2,…，单位为美元)。钢条的长度均为整英寸。图15-1给出了一个价格表的样例。

钢条切割问题是这样的：给定一段长度为n英寸的钢条和一个价格表p_i(i=1,2,…n)，求切割钢条方案，使得销售收益r_n最大。注意，如果长度为n英寸的钢条的价格p_n足够大，最优解可能就是完全不需要切割。

思路

长度为n英寸的钢条共有2^n-1种不同的切割方案，因为在距离钢条左端i(i=1,2,…n)英寸处，总是可以选择切割或不切割。

将钢条切割为长度分别为i₁,i₂...i_k的小段得到的最大收益为r_n=p_i1+p_i2+...+p_ik，则对于n>=1，r_n=max(p_n,r₁+r_n-1,r₂+r_n-2,...,r_n-1+r₁) —— p_n对应不切割，对于每个i=1,2,…,n-1，首先将钢条切割为长度为i和n-i的两段，接着求解这两段的最优切割收益r_i和r_n-i(每种方案的最优收益为两段的最优收益之和)。当完成首次切割后，我们将两段钢条看成两个独立的钢条切割问题实例。通过组合两个相关子问题的最优解，并在所有可能的两段切割方案中选取组合收益最大者，构成原问题的最优解。

递归（自顶向下递归）

钢条切割问题还存在一种相似的但更为简单的递归求解方法：将钢条从左边切割下长度为i的一段，只对右边剩下的长度为n-i的一段继续进行切割，对左边的一段则不再进行切割。这样得到的公式为：r_n=max(p_i+r_n-i), i∈[1,n]。这样原问题的最优解只包含一个相关子问题（右端剩余部分）的解，而不是两个 —— 这个方法的效率很差，运行时间T(n)=T(0)+∑T(j), j∈[0, n=1], T(0)=1，则T(n)=2^n。递归算法之所以效率很低，是因为它反复求解相同的子问题。

动态规划

动态规划有两种等价的实现方法：

• 带备忘的自顶向下法：此方法仍按自然的递归形式编写过程，但过程会保存每个子问题的解（通常保存在一个数组或散列表中）。当需要一个子问题的解时，过程首先检查是否已经保存过此解。如果是，则直接返回保存的值，从而节省了计算时间；否则，按通常方式计算这个子问题。
• 自底向上法：这种方法一般需要恰当定义子问题“规模”的概念，使得任何子问题的求解都只依赖于“更小的”子问题的求解。因此，我们可以将子问题按照规模顺序，由小至大顺序进行求解。当求解某个子问题时，它所依赖的那些更小的子问题都已求解完毕，结果已经保存。每个子问题只需求解一次，当我们求解它时，它的所有前提子问题都已求解完成。

两种方法得到的算法具有相同的渐进运行时间O(n^2)，仅有的差异是在某些特殊情况下，自顶向下方法并未真正递归地考察所有可能的子问题。由于没有频繁的递归函数调用的开销，自底向上方法的时间复杂度函数通常具有更小的系数。

Python 3的实现

递归（自顶向下递归）

def cut_rod(p, n):
    if n == 0:
        return 0
    q = -1
    for i in range(1, n+1):
        q = max(q, p[i] + cut_rod(p, n - i))
    return q

p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
n = 5
q = cut_rod(p, n)
print(q)

#n=1, q=1
#n=2, q=5
#n=3, q=8
#n=4, q=10
#n=5, q=13

动态规划

带备忘的自顶向下法

# Python 3: recursive way with memorized array
def cut_rod(p, n):
    r = [-1] * (n + 1)  # 初始化备忘录
    return cut_rod_aux(p, n, r)


def cut_rod_aux(p, n, r):
    if r[n] >= 0:  # 如果备忘录里存在值，则直接调用并返回。
        return r[n]
    else:
        q = -1
        if n == 0:
            q = 0
        else:
            for i in range(1, n + 1):
                q = max(q, p[i] + cut_rod_aux(p, n - i, r))
        r[n] = q  # 将计算好的结果保存在备忘录里。
        return q

自底向上法

# Python 3: from bottom to up
def cut_rod(p, n):
    r = [-1] * (n + 1) 
    r[0] = 0
    for j in range(1, n + 1):
        q = -1
        for i in range(j + 1):
            q = max(q, p[i] + r[j - i])
        r[j] = q
    return r[n]

重构

之前已经给出了动态规划算法返回最优解的收益值，但没有给出切割后每段钢条的长度（解本身）。下面扩展一下自底向上方法，使之可以报错对应的切割方案。利用这些信息，输出最优解。

def cut_rod_ext(p, n):
    r = [-1] * (n + 1)
    s = [-1] * (n + 1)
    r[0] = 0
    for j in range(1, n + 1):
        q = -1
        for i in range(j + 1):
            if q < p[i] + r[j - i]:
                q = p[i] + r[j - i]
                s[j] = i
        r[j] = q
    return r, s


def print_cut_rod_ext(p, n):
    r, s = cut_rod_ext(p, n)
    while n > 0:
        print(s[n])
        n = n - s[n]

# input:
# n = 7
# output:
# 1
# 6