算法分析（二）算法复杂性

一般来说，最好情况和最坏情况的时间复杂性是很难计量的 —— 原因是对于问题的任意确定的规模N达到了Tmax(N)的合法输入难以确定，而规模N的每一个输入的概率也难以预测或确定。我们有时也按平均情况计量时间复杂性，但那是在对P(I)做了一些人为的假设（比如等概率）之后才进行的。所做的假设是否符合实际总是缺乏根据。因此，在最好情况和平均情况下的时间复杂性分析还仅仅是停留在理论上。

算法复杂性在渐近意义下的阶

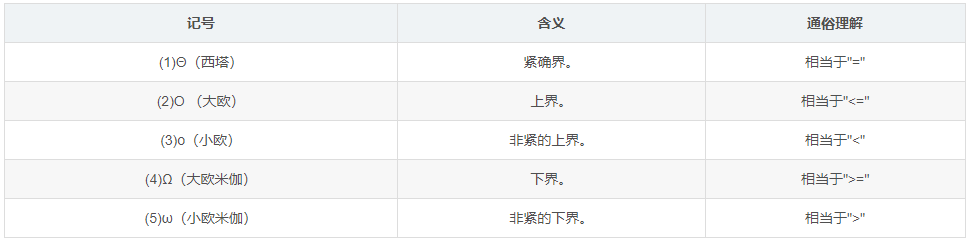
渐近记号Θ、Ο、o、Ω、ω，设f(N)和g(N)是定义在正数集上的正函数。

渐近紧确界记号：Θ（big-theta）

当问题的规模足够大，即例如n=100万，则算法的运行时间主要取决于时间表达式的第一项，并且常系数可以忽略不计，例如：

• 若算法A的运行时间表达式T(n) = 20n⁴+800n³+200n²+1500n+1，则T(n) = Θ(n⁴)
• 若算法B的运行时间表达式T(n) = 100n³+200n²+1500n+1，则T(n) = Θ(n³)

渐近上界记号：O（big-oh）

根据符号O OO的定义，用它评估算法的复杂度得到的只是问题规模充分大时的一个上界。这个上界的阶越低，评估越精确，越有价值。

根据O的定义，容易证明它有如下运算规则：

• O(f)+O(g)=O(max(f,g))
• O(f)+O(g)=O(f+g)
• O(f)O(g)=O(fg)
• 如果g(N)=O(f(N))，则O(f)+O(g)=O(f)
• O(Cf(N))=O(f(N))，其中C是一个正的常数
• f=O(f)

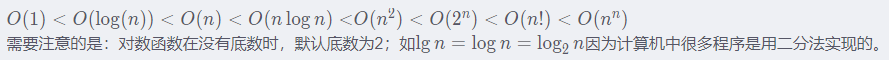
渐近下界记号：Ω（big-omege）

根据符号Ω的定义，用它评估算法的复杂度得到的只是问题规模充分大时的一个下界。这个下界的阶越高，评估越精确，越有价值。

非渐近紧确上界：o（small-oh）

2n²=O(n²)是渐近紧确的，2n=o(n²)是非紧确上界。

非渐近紧确下界：ω（small-omege）

2n²=Ω(n²)是渐近紧确的，2n²=ω(n)是非紧确下界。

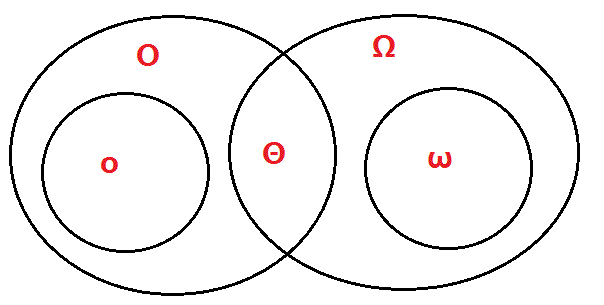
渐近记号Θ、Ο、o、Ω、ω关系

 

算法的时间复杂度（Time Complexity）

时间复杂度（Time Complexity）不是度量具体一个算法具体的耗时是多少。时间复杂度通常用大O表示法，它不包括这个函数的低阶项和首项系数，可以表示为T[n]=O(f(n))，称函数T(n)以f(n)为界或者称T(n)受限于f(n)。 如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)。大O表示法给出的是一个上界，而非一个上确界。

大O符号是由德国数论学家保罗·巴赫曼（Paul Bachmann）在其1892年的著作《解析数论》（Analytische Zahlentheorie）首先引入的。

常见的时间复杂度量级有：

• 常数阶O(1)
• 对数阶O(logN)
• 线性阶O(n)
• 线性对数阶O(nlogN)
• 平方阶O(n²)
• 立方阶O(n³)
• K次方阶O(n^k)
• 指数阶(2^n)

常数阶O(1)

// 无论代码有多少行，只要没有循环等结构，那么时间复杂度就是O(1)。
int x = 13;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;

对数阶O(logN)

public void main()
{
    int i = 1;
    while(i<n)
    {
        // i在每个循环都将乘以2，假设循环x次之后，i就大于n，循环退出，程序结束，那么2^x=n => x=log2(n)，所以时间复杂度为：O(logN)
        i = i * 2;
    }
}

线性阶O(n)

public void main()
{
    int i = 1;
    while(i<n)
    {
        // 执行循环x次后，程序退出，那么x=n => O(n)。
        // 如果i=i+2，时间复杂度同样是O(n)，因为2x=n => O(n/2) => O(n)，因为当n接近于无穷大的时候，常量可以忽略。
        i = i + 1;
    }
}

线性对数阶O(nlogN)

public void main()
{
    int i = 1;
    while(i<n)
    {
        for(int j=1;j<n;j++)
            j = j*2;
    }
}

平方阶O(n²)

public void main()
{
    for(int i=1;i<n;i++)
        for(int j=1;j<n;j++)
            j = j+1;
    }
}

立方阶O(n³)

public void main()
{
    for(int i=1;i<n;i++)
        for(int j=1;j<n;j++)
            for(int k=1;k<n;k++)
                k = k+1;
    }
}

K次方阶O(n^k)

与立方阶O(n³)类似，多层循环。

指数阶(2^n)

比如，旅行商问题（Travelling Salesman Problem，简称TSP）

 

算法的空间复杂度（Space Complexity）

空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。

常见的空间复杂度量级有：

• 常数阶O(1)
• 线性阶O(n)

常数阶O(1)

// 算法执行所需要的空间不随某个变量的大小而变化，则该算法的空间复杂度为一个常量，即O(1)。
int x = 13;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;
x = x + 1;

线性阶O(n)

# include <stdio.h>

int main()
{
    int x[n];
    int i;

    / *初始化数组元素 * /
    for (i = 0; i < n; i++)
    {   
        x[i] = i + 1;
    }

    return 0;
}

参考

1. 算法导论------渐近记号Θ、Ο、o、Ω、ω详解_GNG的博客-CSDN博客_渐进记号