算法思想（一）分治法 Divide & Conquer
分治就是分而治之，就是把一个大问题分成多个相同或相似的子问题，再把子问题分成更小的子问题……直到最后的子问题可以直接求解出来，然后将所有子问题的解的合并，就得到了大问题的解。在分治策略中，我们递归地求解一个问题，在每层递归中应用如下三个步骤：
- 分解（Divide），将问题划分为一些子问题，子问题的形式与原问题一样，只是规模更小。
- 解决（Conquer），递归地求解出子问题。如果子问题的规模足够小，则停止递归，直接求解。
- 合并（Combine），将子问题的解组合成原问题的解。
当子问题最够大，需要递归求解时，我们称之为递归情况（recursive case）。当子问题变得足够小，不再需要递归时，就已经“触底”，进入了基本情况（base case）。有时，除了与原问题形式完全一样的规模更小的子问题之外，还需要求解与原问题不完全一样的子问题。我们将这些子问题看做合并步骤的一部分。分治法能解决的问题一般具有以下几个特征：
- 该问题的规模缩小到一定的程度就可以容易地解决。
- 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
- 利用该问题分解出的子问题的解可以合并为该问题的解。
- 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。
上述的第一条特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加；第二条特征是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用；第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。
常见用分治法求解的问题
- 最大子数组问题
- 矩阵乘法的Strassen算法
- 用代入法求解递归式
- 用递归树方法求解递归式
- 用主方法求解递归式
伪代码
divide-and-conquer(P) { if ( | P | <= n0) adhoc(P); //解决小规模的问题 divide P into smaller subinstances P1,P2,...,Pk；//分解问题 for (i=1,i<=k,i++) yi=divide-and-conquer(Pi); //递归的解各子问题 return merge(y1,...,yk); //将各子问题的解合并为原问题的解 }
人们从大量实践中发现，在用分治法设计算法时，最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡(balancing)子问题的思想，它几乎总是比子问题规模不等的做法要好。
复杂性分析
一个分治法将规模为n的问题分成k个规模为n／m的子问题去解。设分解阀值n0=1，且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有：
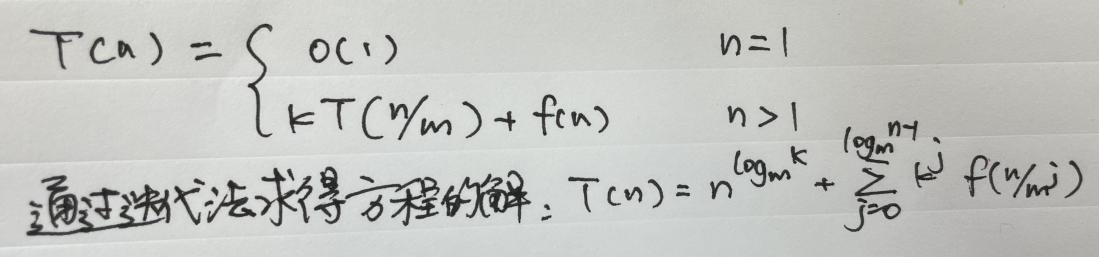
几种变形
- 二分法 dichotomy：一种每次将原问题分解为两个子问题的分治法，是一分为二的哲学思想的应用。这种方法很常用，由此法产生了许多经典的算法和数据结构。
- 分解并在解决之前合并法 divide and marriage before conquest：一种分治法的变形，其特点是将分解出的子问题在解决之前合并。
- 管道传输分治法 pipelined divide and conquer：一种分治法的变形，它利用某种称为“管道”的数据结构在递归调用结束前将其中的某些结果返回。此方法经常用来减少算法的深度。
