移位密码(Shift Cipher)体制的加密、解密和破解
移位密码的理论基础是数论中的模运算。
模运算的基本定义:假设a和b均为整数,m是一正整数。若m整除a-b,则可将其表示为a≡b(mod m),正整数m称为模数。
模运算m上的算术运算定义:令
表示集合{0,1,...,m-1},在其上定义两个运算,加法(+)和乘法(x) —— 运算类似于普通的实数域上的加法和乘法,所不同的只是所得的值是取模以后的余数。
因为英文有26个字母,故其一般定义在![]() ,则容易验证移位密码满足所定义的密码体制1.1的条件,即对任意的x∈
,则容易验证移位密码满足所定义的密码体制1.1的条件,即对任意的x∈![]() ,都有
,都有![]() 。
。
若取K=3,则次密码体制通常叫做凯撒密码(Caesar Cipher),因为它首先被儒勒·凯撒所使用。
使用移位密码来加密普通的英文句子,首先必须要建立英文字母和模26剩余之间的一一对应关系:如A=1,B=2,...Z=25,如下表所示:
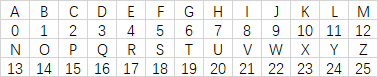
例如,假设移位密码的密钥为K=11,明文为wewillmeetatmidnight。
首先将明文中的字母对应于其相应的整数,得到如下数字串:
22 04 22 08 11 11 12 04 04 19
00 19 12 08 03 13 08 06 07 19
然后,将每个数都与11相加,再对其和取模26运算,可得:
07 15 07 19 22 22 23 15 15 04
11 04 23 19 14 24 19 17 18 04
最后,再将其转换为相应的字符串,即得到密文为HPHTWWXPPELEXTOYTRSE。
要对密文进行解密,只需执行相应的逆过程即可。
但是,移位密码(模26)是不安全的,可用密钥穷尽搜索方法来破译,因为密钥空间太小,只有26种可能的情况,可以穷举所有的可能密钥,得到我们所希望的有意义的明文来。
代码实现(Python 3)
'''暴力破解移位密码''' def hack_shift_cipher(text :str): SYMBOLS = 'abcdefghijklmnopqrstuvwxyz' for key in range(27): translated = '' for symbol in text: symbol = symbol.lower() if symbol in SYMBOLS: symbolIndex = SYMBOLS.find(symbol) translatedIndex = (symbolIndex - key ) %26 translated = translated + SYMBOLS[translatedIndex] else: translated = translated + symbol print(f'key={key}: {translated}') '''移位密码体制加密''' def shift_cipher_encrypt(text: str, key = 13): SYMBOLS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' translated = '' for symbol in text: symbol = symbol.upper() if symbol in SYMBOLS: symbolIndex = SYMBOLS.find(symbol) translatedIndex = (symbolIndex + key ) %26 translated = translated + SYMBOLS[translatedIndex] else: translated = translated + symbol print(translated) '''移位密码体制解密''' def shift_cipher_decrypt(text: str, key = 13): SYMBOLS = 'abcdefghijklmnopqrstuvwxyz' translated = '' for symbol in text: symbol = symbol.lower() if symbol in SYMBOLS: symbolIndex = SYMBOLS.find(symbol) translatedIndex = (symbolIndex - key ) %26 translated = translated + SYMBOLS[translatedIndex] else: translated = translated + symbol print(translated)

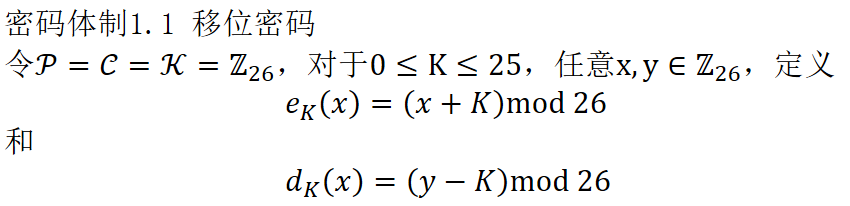

 浙公网安备 33010602011771号
浙公网安备 33010602011771号