排序算法（四）归并排序

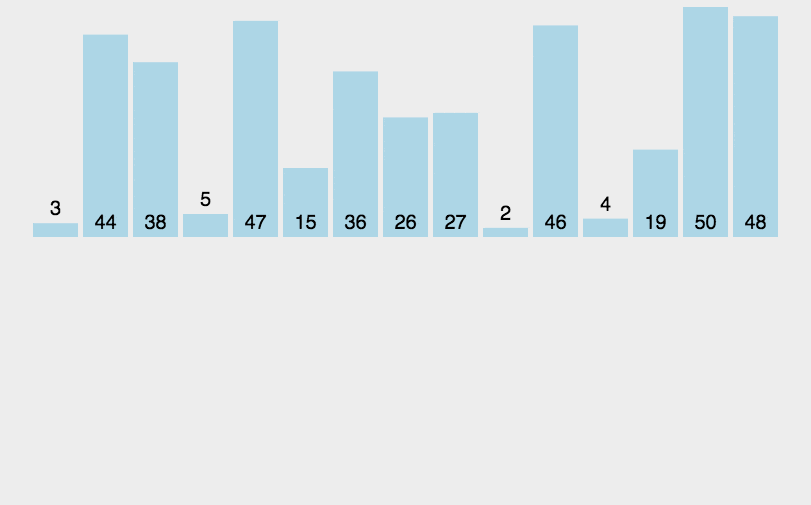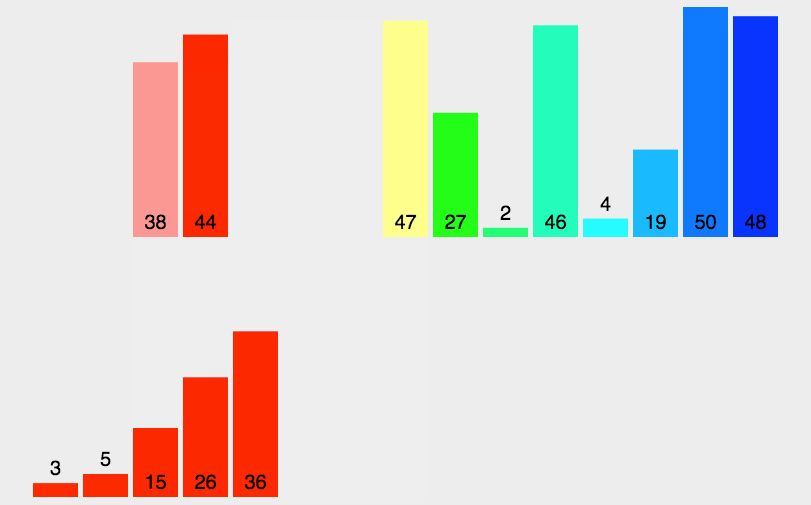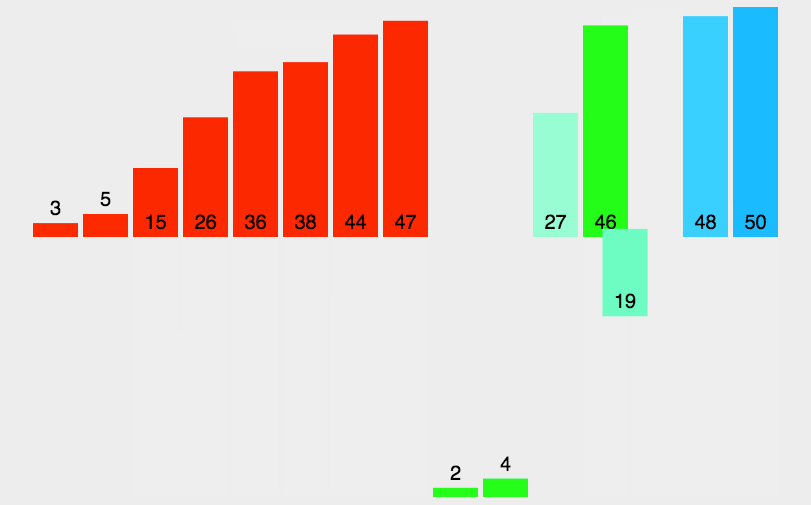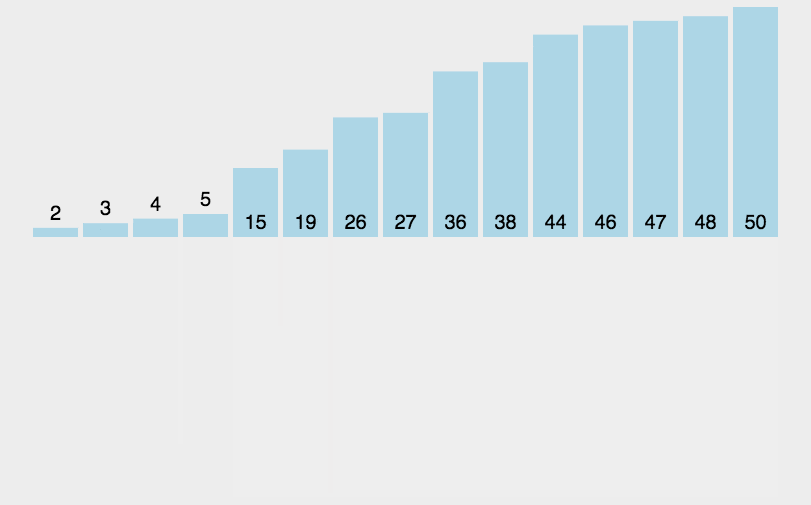
归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法，是采用分治法（Divide and Conquer）的一个非常典型的应用。

时间复杂度：O(NlogN)

空间复杂度：O(N)

稳定性：稳定

// C: 归并排序
void merge_sort(int list[], int n) {
    /* perform a merge sort on the list. */
    int length = 1;
    int extra[100];

    while (length < n) {
        merge_pass(list, extra, n, length);
        length *= 2;
        merge_pass(extra, list, n, length);
        length *= 2;
    }
}


// 归并排序： 归并两个已排序的表，例如：int sorted_list[10] = { 2,3,5,6,9,1,4,10,12,14 }，则 merge(sorted_list, sorted, 0, 4, 9);
void merge(int list[], int sorted[], int i, int m, int n) {
    /* merge two sorted lists: list[i], ..., list[m], and
    list[m+1], ..., list[n]. These lists are sorted to
    obtain a sorted list: sorted[i], ..., sorted[n] */
    int j, k, t;
    j = m + 1;
    k = i;
    while (i <= m && j <= n) {
        if (list[i] <= list[j])
            sorted[k++] = list[i++];
        else
            sorted[k++] = list[j++];
    }
    if (i > m)
        /* sorted[k], ... , sorted[n] = list[j], ..., list[n] */
        for (t = j; t <= n; t++)
            sorted[k + t - j] = list[t];
    else
        /* sorted[k], ... , sorted[n] = list[i], ..., list[m] */
        for (t = i; t <= m; t++)
            sorted[k + t - i] = list[t];
}


// 单次归并排序
void merge_pass(int list[], int sorted[], int n, int length) {
    /* perform one pass of the merge sort. It merges adjacent
    pairs of sub-lists from list into sorted. n is the 
    number of elements in the list. length is the length of the
    sub-list. */
    int i, j;
    for (i = 0; i <= n - 2 * length; i += 2 * length)
        merge(list, sorted, i, i + length - 1, i + 2 * length - 1);
    if (i + length < n)
        merge(list, sorted, i, i + length - 1, n - 1);
    else
        for (j = i; j < n; j++)
            sorted[j] = list[j];
}

 

# Python 3: 归并排序
def merge_sort(arr):
    import math
    if len(arr)<2:
        return arr
    middle = math.floor(len(arr)/2)
    left, right = arr[0:middle], arr[middle:]
    return merge(merge_sort(left), merge_sort(right))

def merge(left,right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    while left:
        result.append(left.pop(0))
    while right:
        result.append(right.pop(0))
    return result