线段树--天才绅士少女助手克里斯蒂娜
又是线段树……应该是近期写的第五道线段树
这道题的难点在于式子推导,虽然我并不会自己推,但是可以证明正确性:
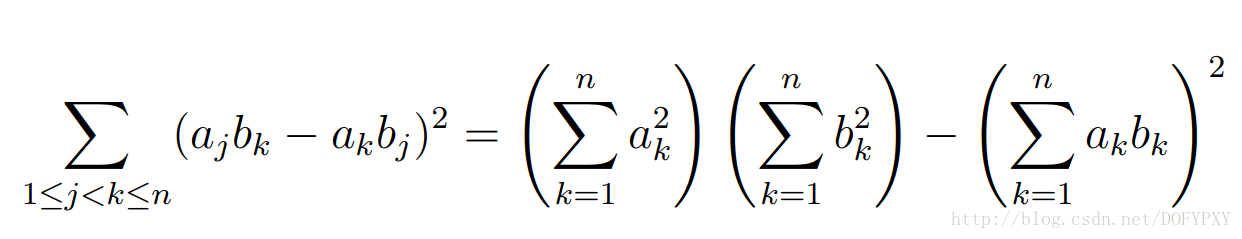
于是就可以维护三个线段树,表示三个式子,直接写线段树就好了,唯一需要注意的地方就是取模,为了避免负数,我们可以写成 也有必要写成(x%mod+mod)%mod,不然输出不正确,最后记得开long long
代码:
1 #include <iostream>
2 #include <cstdio>
3 #include <algorithm>
4 using namespace std;
5 #define ll long long
6 ll n,m;
7 const int maxn=1e7;
8 ll mod=20170927;
9 ll x0[maxn],y0[maxn],tree[5][maxn],mark,p,x1,y1,l,r;
10 inline ll ls(ll x){return x<<1;}
11 inline ll rs(ll x){return x<<1|1;}
12 inline void pushup(ll x){
13 for (ll i = 1;i <= 3;i++) tree[i][x]=(tree[i][ls(x)]+tree[i][rs(x)])%mod;
14 }
15 inline void build(ll x,ll l,ll r){
16 if (l==r){
17 tree[1][x]=x0[l]*x0[l]%mod;tree[2][x]=y0[l]*y0[l]%mod;tree[3][x]=x0[l]*y0[l]%mod;return;
18 }
19 ll mid=(l+r)>>1;
20 build(ls(x),l,mid);build(rs(x),mid+1,r);
21 pushup(x);
22 // for (int i = 1;i <= 3;i++) cout<<tree[i][x]<<endl;
23 }
24 inline void update(ll x,ll l,ll r,ll pos,ll x1,ll y1){
25 if (l==r&&l==pos){
26 tree[1][x]=x1*x1%mod;tree[2][x]=y1*y1%mod;tree[3][x]=x1*y1%mod;return;
27 }
28 ll mid=(l+r)>>1;
29 if (pos<=mid) update(ls(x),l,mid,pos,x1,y1);
30 if (pos>mid) update(rs(x),mid+1,r,pos,x1,y1);
31 pushup(x);
32 }
33 inline ll query(ll x,ll l,ll r,ll nl,ll nr,ll num){
34 ll ans=0;
35 if (nl<=l&&r<=nr) return tree[num][x];
36 ll mid=(l+r)>>1;
37 if (nl<=mid) ans+=query(ls(x),l,mid,nl,nr,num);
38 if (nr>mid) ans+=query(rs(x),mid+1,r,nl,nr,num);
39 return ans;
40 }
41 int main(){
42 scanf ("%d%d",&n,&m);
43 for (ll i = 1;i <= n;i++) scanf ("%d%d",&x0[i],&y0[i]);
44 build(1,1,n);
45 for (ll i = 1;i <= m;i++){
46 cin>>mark;
47 if (mark==1){
48 cin>>p>>x1>>y1;
49 update(1,1,n,p,x1,y1);
50 }
51 else {
52 cin>>l>>r;
53 ll sum1=query(1,1,n,l,r,1),sum2=query(1,1,n,l,r,2),sum3=query(1,1,n,l,r,3);
54 ll ans1=((sum1*sum2)%mod+mod)%mod,ans2=((sum3*sum3)%mod+mod)%mod;
55 // cout<<sum1<<endl<<sum2<<endl<<sum3<<endl;
56 ll ans=((ans1-ans2)%mod+mod)%mod;
57 cout<<abs(ans)<<endl;
58 }
59 }
60 return 0;
61 }





