最短路问题-- Dijkstra Choose the best route

Choose the best route

Problem Description

One day , Kiki wants to visit one of her friends. As she is liable to carsickness , she wants to arrive at her friend’s home as soon as possible . Now give you a map of the city’s traffic route, and the stations which are near Kiki’s home so that she can take. You may suppose Kiki can change the bus at any station. Please find out the least time Kiki needs to spend. To make it easy, if the city have n bus stations ,the stations will been expressed as an integer 1,2,3…n.

Input

There are several test cases.
Each case begins with three integers n, m and s,(n<1000,m<20000,1=<s<=n) n stands for the number of bus stations in this city and m stands for the number of directed ways between bus stations .(Maybe there are several ways between two bus stations .) s stands for the bus station that near Kiki’s friend’s home.
Then follow m lines ,each line contains three integers p , q , t (0<t<=1000). means from station p to station q there is a way and it will costs t minutes .
Then a line with an integer w(0<w<n), means the number of stations Kiki can take at the beginning. Then follows w integers stands for these stations.

 

Output

The output contains one line for each data set : the least time Kiki needs to spend ,if it’s impossible to find such a route ,just output “-1”.

 

$Dijkstra$ 算法：以点为思考中心的最短路径算法。

图结构存储：邻接表

流程：1.初始化

const int INF = 1e9; 
bool hasFind[maxn]; 
for (int i = 0 ;i<= n ;i++) 
    dist[i] = INF; 
dist[sNode] = 0; 
memset(hasFind,0,sizeof hasFind); 
hasFind[sNode] = true;

具体流程为：

for (int i = 0 ;i< n-1 ;i++){ 
    int nId = -1 ; 
    for (int j = 0 ;j< n ;j++){ 
        if (!hasFind[j]){ 
            if (nId == -1) 
                nId = j; 
            else if (dist[j]<dist[nId]) 
                nId = j; 
            } 
        } 
        hasFind[nId] = true; 
    for (int i = 0 ;i< node[nId].size() ;i++){
        int nextId = node[nId][i].nextId; 
        if (node[nId][i].dist + dist[nId]< dist[nextId]){ 
            dist[nextId] = node[nId][i].dist + dist[nId]; 
            que.push(nextId); 
            }
    }
}

 时间复杂度 节点个数 $N$，边个数 $M$ $O$($N\times N$)

 举例 • 求所有节点到节点 1 的最短距离

 

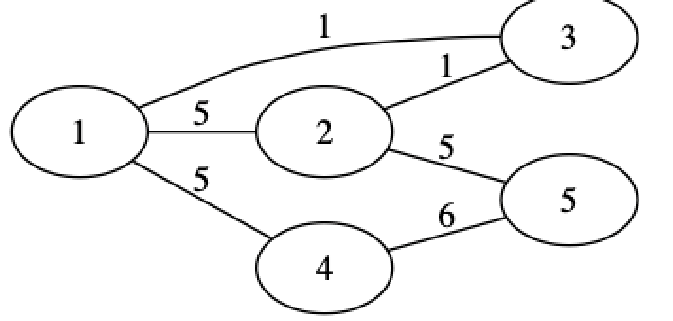
 1. 初始化
• 将源节点 1，放入已获取最短路径集合, 集合变为 {1}

• 未获取最短路径节点结合 {2,3,4,5}

• 根据节点 1 来更新所有节点距离源节点的距离 $dist$

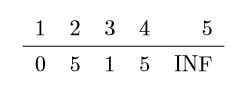
2. 流程
(a) $step$ 1:

• 从未获取最短路径节点结合 {2,3,4,5} 中，选取距离源节点最 近的节点 3

• 将节点 3，放入已获取最短路径集合, 集合变为 {1,3}

• 根据节点 3 来更新所有节点距离源节点的距离 $dist$

 

 

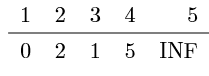
 (b) $step$ 2:

• 从未获取最短路径节点结合 {2,4,5} 中，选取距离源节点最 近的节点 2

• 将节点 2，放入已获取最短路径集合, 集合变为 {1,2,3}

• 根据节点 2 来更新所有节点距离源节点的距离 $dist$

 

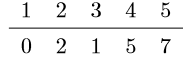
 (c) $step$ 3:

• 从未获取最短路径节点结合 {4,5} 中，选取距离源节点最近 的节点 4

• 将节点 4，放入已获取最短路径集合, 集合变为 {1,2,3,4}

• 根据节点 4 来更新所有节点距离源节点的距离 $dist$

 

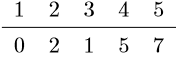
 (d) $step$ 4:

• 从未获取最短路径节点结合 {5} 中，选取距离源节点最近的 节点 5

• 将节点 5，放入已获取最短路径集合, 集合变为 {1,2,3,4,5}

• 根据节点 5 来更新所有节点距离源节点的距离 $dist$

 

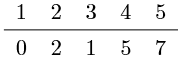
 (e) 终止条件，所有节点都放入到了已获取最短路径集合。

把所有部分合并在一起得到一段代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#define Inf 0x3f3f3f3f
 
using namespace std;
int map[1005][1005];
int vis[1005],dis[1005];
int n,m;//n个点，m条边
void Init ()
{
    memset(map,Inf,sizeof(map));
    for(int i=1;i<=n;i++)
    {
        map[i][i]=0;
    }
}
void Getmap()
{
    int u,v,w;
    for(int t=1;t<=m;t++)
    {
          scanf("%d%d%d",&u,&v,&w);
          if(map[u][v]>w)
          {
          map[u][v]=w;
          map[v][u]=w;
          }
    }    
}
 
void Dijkstra(int u)
{
    memset(vis,0,sizeof(vis));
    for(int t=1;t<=n;t++)
    {
        dis[t]=map[u][t];
    }
    vis[u]=1;
    for(int t=1;t<n;t++)
    {
        int minn=Inf,temp;
        for(int i=1;i<=n;i++)
        {
            if(!vis[i]&&dis[i]<minn)
            {
                minn=dis[i];
                temp=i;
            }
        }
        vis[temp]=1;
        for(int i=1;i<=n;i++)
        {
            if(map[temp][i]+dis[temp]<dis[i])
            {
                dis[i]=map[temp][i]+dis[temp];
            }
        }
    }
}
 
int main()
{
    
    scanf("%d%d",&m,&n);
    Init();
    Getmap();
    Dijkstra(n);
    printf("%d\n",dis[1]);    
    return 0;
}

 

这道题的代码如下：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdlib>
using namespace std;

const int INF=0x3f3f3f3f;
const int N=1010;
int mp[N][N];
int dis[N];
int vis[N];
int m;
int n;
int dijstra()
{
    memset(dis,0x3f,sizeof(dis));
    memset(vis,0,sizeof(vis));
    dis[0]=0;
    for(int i=1;i<=n;i++)
    {
        int k=0;
        int mini=INF;
        for(int j=1;j<=n;j++)
        {
            if(!vis[j]&&mini>dis[j])
                mini=dis[k=j];
        }
        vis[k]=1;
        if(k==m) return dis[m];
        for(int j=1;j<=n;j++)
        {
            if(vis[j]||mp[k][j]==INF) continue;
            dis[j]=min(dis[j],dis[k]+mp[k][j]);
        }
    }
    return dis[m];
}
int main()
{
    int s;         //已修好的路有几条
    while(~scanf("%d%d%d",&n,&s,&m))    //终点是m，最远的点是n
    {
        memset(mp,INF,sizeof(mp));
        while(s--)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            if(mp[a][b]>c)
                mp[a][b]=c;
        }
        int d;      
        scanf("%d",&d);
        while(d--)
        {
            int x;      
            scanf("%d",&x);
            mp[0][x]=0;      
        }
        int k=dijstra();
        if(k==INF) printf("-1\n");
        else printf("%d\n",dijstra());
    }
    return 0;
}