好题选讲(3)
[TC SRM554Hard] TheBrickTower
Description
给你一些 $1\times 1\times1$ 的方块,有 $C$ 种颜色,定义一座 $2\times2\times h$ 的塔的高度为 $h$ ,求所有高度不超过 $H$ 的塔且相邻小方块颜色相同的组数不超过 $k$ 的方案数。
$C\le 4747,k\le7,H\le474747474747$
Sol
设 $f_{i,j,k}$ 代表高度不超过 $i$ 的塔,一共有 $j$ 对相同的块相邻,最上面一层摆放方式为 $k$ ,容易看出要用矩阵快速幂转移。
通过打表,我们可知不同的摆放方式只有 $15$ 种,那么 $j,k$ 的对数不超过 $105$ 对,于是可以通过暴搜来处理转移矩阵。
这道题需要两次暴搜,细节比较多,可以看代码理解。
Code

#include<bits/stdc++.h> #define Mod 1234567891 using namespace std; long long Read() { long long x = 0, f = 1; char ch = getchar(); while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();} while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();} return x * f; } long long c, k, h, lim, pos[5], mod[4] = {1, 4, 16, 64}; struct martix { long long a[155][155]; martix(){memset(a, 0, sizeof(a));} martix operator * (martix A) { martix B; memset(B.a, 0, sizeof(B.a)); for(long long i = 0; i <= lim; i++) for(long long j = 0; j <= lim; j++) for(long long k = 0; k <= lim; k++) { B.a[i][j] += a[i][k] * A.a[k][j] % Mod; B.a[i][j] %= Mod; } return B; } }; martix qpow(martix a, long long b) { martix res; for(long long i = 0; i <= lim; i++) res.a[i][i] = 1; while(b) { if(b & 1) res = res * a; a = a * a; b >>= 1; } return res; } struct node { long long val, k, usd, pos[5]; node(long long Val = 0, long long K = 0, long long Usd = 0){val = Val, k = K, usd = Usd;} }; vector<node> v; long long Calc(long long val, long long x) { if(x != 3) val %= mod[x + 1]; return val / mod[x]; } long long Calc_k(node A) {return (A.pos[0] == A.pos[3]) + (A.pos[1] == A.pos[0]) + (A.pos[2] == A.pos[1]) + (A.pos[3] == A.pos[2]);} void dfs1(long long nw, long long usd, long long val) { if(nw == 4) { node t; t.val = val, t.usd = usd; for(long long i = 0; i < 4; i++) t.pos[i] = Calc(val, i); t.k = Calc_k(t); if(t.k > k) return ; v.push_back(t); return ; } for(long long i = 0; i < usd; i++) dfs1(nw + 1, usd, val + i * mod[nw]); if(usd < c) dfs1(nw + 1, usd + 1, val + usd * mod[nw]); } long long sel[5], vis[5], p1, p2, vt, cnt1, cnt2, tot; node t1, t2; martix e; long long fac(long long n, long long t) {return (t == 1) ? n % Mod : ((t == 0) ? 1ll : fac(n - 1, t - 1) * n % Mod);} void dfs(long long nw, long long _dif, long long _cnt) { if(nw == 4) { for(long long i = cnt1; i <= k; i++) { if(i + _cnt + cnt2 > k) return ; long long t = fac(c - t1.usd, _dif); (e.a[p1 + tot * i][lim] += t) %= Mod; (e.a[p1 + tot * i][p2 + tot * (i + _cnt + cnt2)] += t) %= Mod; } return ; } for(long long i = 0; i < nw; i++) { if(t2.pos[i] == t2.pos[nw]) { sel[nw] = sel[i]; dfs(nw + 1, _dif, _cnt + (sel[i] == t1.pos[nw])); return ; } } if(_dif + t1.usd < c) { sel[nw] = 4; dfs(nw + 1, _dif + 1, _cnt); } for(long long i = 0; i < t1.usd; i++) { if(vis[i] == vt) continue; vis[i] = vt; sel[nw] = i; dfs(nw + 1, _dif, _cnt + (sel[nw] == t1.pos[nw])); vis[i] = 0; } } void trans(long long pos1, long long pos2) { p1 = pos1, p2 = pos2; cnt1 = v[p1].k, cnt2 = v[p2].k; if(cnt1 + cnt2 > k) return ; t1 = v[p1], t2 = v[p2]; ++vt; dfs(0, 0, 0); } class TheBrickTowerHardDivOne { public: int find(int C, int K, long long H) { c = C, k = K, h = H; dfs1(1, 1, 0); tot = v.size(), lim = tot * (k + 1); for(long long i = 0; i < tot; i++) for(long long j = 0; j < tot; j++) trans(i, j); martix a; for(long long i = 0; i < tot; i++) { node t3 = v[i]; (a.a[0][i + t3.k * tot] += fac(c, t3.usd)) %= Mod; (a.a[0][lim] += fac(c, t3.usd)) %= Mod; } e.a[lim][lim] = 1; a = a * qpow(e, h - 1); return (int)a.a[0][lim]; } };
[HDU5564] Clarke and digits
Description
求出所有位数在 $[l,r]$ 间且能被 $7$ 整除且任意相邻两位之和不为 $k$ 的数的个数。
$l,r\le 10^9,k\le18$
Sol
首先考虑暴力 $\mathcal{O}(700r)$ 的 DP 方程式,设 $f_{i,j,k}$ 表示位数为 $i$ ,除 $7$ 余数为 $j$ ,最后一位为 $k$ 的数的个数。
枚举 $m\in[0,9]$ 那么我们有:
$$f_{i+1,(10j+m),m}=\sum f_{i,j,k}$$
考虑 $j,k$ 的范围很小,可以矩阵快速幂,由于要求前缀和,所以矩阵可以加一行代表和的行,用三层 for 循环处理所有 $j,k$ 的转移方式即可。
Code

#include<bits/stdc++.h> #define int long long #define Mod 1000000007 using namespace std; int Read() { int x = 0, f = 1; char ch = getchar(); while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();} while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();} return x * f; } int lim; struct martix { int a[155][155]; void init(int x) { memset(a, 0, sizeof(a)); for(int i = 0; i < lim; i++) a[i][i] = x; } martix operator * (martix A) { martix B; B.init(0); for(int i = 0; i < lim; i++) for(int j = 0; j < lim; j++) for(int k = 0; k < lim; k++) (B.a[i][j] += a[i][k] * A.a[k][j]) %= Mod; return B; } }; martix operator ^ (martix a, int b) { martix res; res.init(1); while(b) { if(b & 1) res = res * a; a = a * a; b >>= 1; } return res; } signed main() { lim = 71; int T = Read(); while(T--) { martix A, B; B.init(0), A.init(0); int l = Read(), r = Read(), k = Read(); for(int i = 0; i < 7; i++) for(int j = 0; j <= 9; j++) for(int x = 0; x <= 9; x++) if(j + x != k) ++B.a[i * 10 + j][((i * 10 + x) % 7) * 10 + x]; for(int i = 0; i <= 9; i++) ++B.a[i][lim - 1]; B.a[lim - 1][lim - 1] = 1; for(int i = 1; i <= 9; i++) ++A.a[0][(i % 7) * 10 + i]; martix a = A * (B ^ (r)), b = A * (B ^ (l - 1)); cout << (a.a[0][lim - 1] - b.a[0][lim - 1] + Mod) % Mod << endl; } return 0; }
[bzoj2510] 弱题
Description
有 $M$ 个球,一开始每个球均有一个初始标号,标号范围为 $[1,n]$ 且为整数,标号为 $i$ 的球有 $a_i$ 个,并保证 $\sum a_i=M$。
每次操作等概率取出一个球(即取出每个球的概率均为 $\frac 1m$ ),若这个球标号为 $k(k\le n)$,则将它重新标号为 $k+1$;若这个球标号为 $N$,则将其重标号为 $1$。(取出球后并不将其丢弃)
求出经过 $K$ 次这样的操作后,每个标号的球的期望个数。
$M\le10^8,N\le1000,K\le 21471483647$
Sol
考虑 DP ,设 $f_{i,j}$ 表示第 $i$ 轮标号为 $j$ 的球的期望个数,那么有暴力 DP 方程式:
$$f_{i,j}=\frac{M-1}{M}f_{i-1,j}+\frac 1M f_{i-1}{j-1}$$
用矩阵快速幂优化,发现转移矩阵长的很有规律:
$$\begin{bmatrix} \frac{M-1}{M} & \frac 1M & 0 & 0 & ... & 0 \\ 0 & \frac{M-1}{M} & \frac 1M & 0 & ... & 0 \\ 0 & 0 & \frac{M-1}{M} & \frac 1M & ... &0 \\ ... & ... & ... & ... & ... & ... \\ \frac 1M & 0 & 0 & 0 & ... & \frac{M-1}{M} \end{bmatrix}$$
所以我们可以只保留矩阵的第一行,进行 $\mathcal{O} (n^2)$ 矩阵乘法即可。
Code

#include<bits/stdc++.h> #define int long long #define Mod 1000000007 using namespace std; int Read() { int x = 0, f = 1; char ch = getchar(); while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();} while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();} return x * f; } int lim; struct martix { int a[155][155]; void init(int x) { memset(a, 0, sizeof(a)); for(int i = 0; i < lim; i++) a[i][i] = x; } martix operator * (martix A) { martix B; B.init(0); for(int i = 0; i < lim; i++) for(int j = 0; j < lim; j++) for(int k = 0; k < lim; k++) (B.a[i][j] += a[i][k] * A.a[k][j]) %= Mod; return B; } }; martix operator ^ (martix a, int b) { martix res; res.init(1); while(b) { if(b & 1) res = res * a; a = a * a; b >>= 1; } return res; } signed main() { lim = 71; int T = Read(); while(T--) { martix A, B; B.init(0), A.init(0); int l = Read(), r = Read(), k = Read(); for(int i = 0; i < 7; i++) for(int j = 0; j <= 9; j++) for(int x = 0; x <= 9; x++) if(j + x != k) ++B.a[i * 10 + j][((i * 10 + x) % 7) * 10 + x]; for(int i = 0; i <= 9; i++) ++B.a[i][lim - 1]; B.a[lim - 1][lim - 1] = 1; for(int i = 1; i <= 9; i++) ++A.a[0][(i % 7) * 10 + i]; martix a = A * (B ^ (r)), b = A * (B ^ (l - 1)); cout << (a.a[0][lim - 1] - b.a[0][lim - 1] + Mod) % Mod << endl; } return 0; }
[bzoj1563] 诗人小G
Description

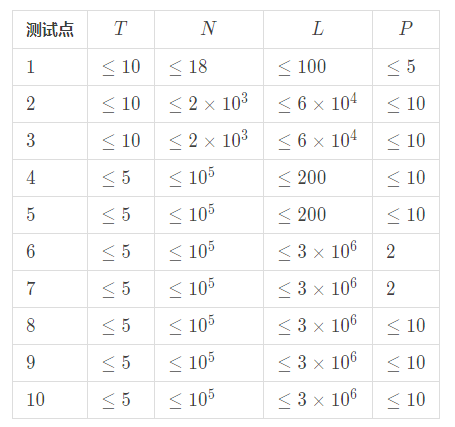
Sol
先考虑暴力 DP,设 $f_i$ 表示处理到第 $i$ 句诗的最小花费,那么枚举 $j\in[1,i)$,我们有 $f_i=\max{f_j+calc(i,j)}$。
打表可知此题 DP 的决策点(即每一次转移过来的 $j$)是单调递增的,那么我们可以二分这个决策点。
令三元组 $(x,l,r)$ 表示 $f_l$ 到 $f_r$ 均是由 $x$ 转移过来的,我们用单调队列存,初始只有 $(0,1,n)$ 。
每当放入一个新的决策点,我们就枚举该点与上一个决策点的关系,如果完全覆盖则从队尾排出。如果完全没有覆盖则结束枚举,如果覆盖了一些区域则二分当前决策点的位置,并将新的三元组放入队列,顺便更新 $f_i$ 。
输出解时就顺便记录一下是从哪一个决策点转移过来的就行了。
Code

#include<bits/stdc++.h> #define int long long #define double long double using namespace std; int Read() { int x = 0, f = 1; char ch = getchar(); while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();} while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();} return x * f; } int n, l, p, f[100005]; double dp[500005], s[500005]; char ch[100005][55]; double qpow(double a, int b) { double res = 1; while(b) { if(b & 1) res = res * a; a = a * a; b >>= 1; } return res; } double Calc(int st, int ed) { return dp[st] + qpow(abs(s[ed] - s[st] - l - 1), p); } int q[500005], head, tail, lef[500005], rig[500005], trans[500005], stk[500005]; signed main() { int T = Read(); while(T--) { memset(s, 0, sizeof(s)); memset(f, 0, sizeof(f)); memset(lef, 0, sizeof(lef)); memset(rig, 0, sizeof(rig)); memset(trans, 0, sizeof(trans)); memset(stk, 0, sizeof(stk)); memset(ch, 0, sizeof(ch)); memset(q, 0, sizeof(q)); n = Read(), l = Read(), p = Read(); for(int i = 1; i <= n; i++) { scanf("%s", ch[i] + 1); s[i] = s[i - 1] + strlen(ch[i] + 1) + 1; } head = 1, tail = 0; q[++tail] = 0, lef[0] = 1, rig[0] = n; for(int i = 1; i <= n; i++) { while(head <= tail && rig[q[head]] < i) ++head; trans[i] = q[head]; dp[i] = Calc(q[head], i); while(head <= tail && Calc(i, lef[q[tail]]) <= Calc(q[tail], lef[q[tail]])) --tail; int l = lef[q[tail]], r = n, pos = -1; while(l <= r) { int mid = (l + r + 1) >> 1; if(Calc(i, mid) <= Calc(q[tail], mid)) r = mid - 1, pos = mid; else l = mid + 1; } if(pos == -1) continue; rig[q[tail]] = pos - 1; q[++tail] = i; lef[i] = pos, rig[i] = n; } if(dp[n] > 1e18) puts("Too hard to arrange"); else { printf("%lld\n", (long long)dp[n]); int tp = 0, tmp = 0; for(int i = n; i; i = trans[i]) stk[++tp] = i; for(int i = 1; i <= n; i++) { if(tmp) putchar(' '); printf("%s", ch[i] + 1); if(i == stk[tp]) puts(""), --tp, tmp = 0; else ++tmp; } } puts("--------------------"); } return 0; }
[bzoj3473] Kamp
Description
一棵 $N$ 个点的树,有 $K$ 个特殊点,询问从每个点出发到达所有特殊点一次的最短路。
$k\le n\le 5\times 10^5$
Sol
换根 DP,记 $fans_u$ 表示点 $u$ 经过 $u$ 子树所有特殊点再回到 $u$ 的最短路,$ans_u$ 表示点 $u$ 经过所有特殊点回到 $u$ 的最短路。
那么对于 $u$ 的每个儿子 $v$ ,如果 $v$ 的子树内有特殊点的话,那么 $fans_u=\sum_{v\in son{u}} fans_v+2\times w(u,v)$
再来一遍 dfs 处理 $ans$,我们分三种情况讨论:
- 当 $sz_v=0$ 时,我们必将通过边 $(v,u)$ 走到 $u$ ,再通过 $u$ 走到所有特殊点,故 $ans_v=ans_u+2\times w(u,v)$
- 当 $sz_v=k$ 时,所有特殊点都在 $v$ 子树内,故 $ans_v=fans_v$。
- 当 $sz_v\in(0,k)$ 时,$ans_v=ans_u$。
因为最终不用返回 $u$ 点,所以还需要预处理最长链,具体实现比较复杂,建议看代码理解。
Code

#include<bits/stdc++.h> #define int long long using namespace std; int Read() { int x = 0, f = 1; char ch = getchar(); while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();} while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();} return x * f; } int first[1000005], nxt[1000005], to[1000005], w[1000005], tot; void Add(int x, int y, int z) { nxt[++tot] = first[x]; first[x] = tot; to[tot] = y; w[tot] = z; } int n, k, f[500005], g[500005], h[500005], sz[500005], isg[500005], flg[500005]; int ans[500005], fans[500005]; void dfs1(int u, int fa) { sz[u] = isg[u]; f[u] = (isg[u] ? 0 : -1); for(int e = first[u]; e; e = nxt[e]) { int v = to[e]; if(v == fa) continue; dfs1(v, u); sz[u] += sz[v]; if(sz[v]) fans[u] += fans[v] + 2 * w[e]; if(f[v] != -1) { if(f[v] + w[e] > f[u]) flg[u] = 0, f[u] = f[v] + w[e]; else if(f[v] + w[e] == f[u]) flg[u] = 1; } } } void dfs2(int u, int fa) { int maxx = -1; for(int e = first[u]; e; e = nxt[e]) { int v = to[e]; if(v == fa) continue; if(sz[v] == 0) ans[v] = ans[u] + 2 * w[e]; else if(sz[v] == k) ans[v] = fans[v]; else ans[v] = ans[u]; dfs2(v, u); if(f[u] == -1) continue; if(flg[u]) h[v] = f[u]; else if(f[v] == -1 || f[v] + w[e] != f[u]) { h[v] = f[u]; if(f[v] != -1) maxx = max(maxx, f[v] + w[e]); } } if(flg[u]) return ; for(int e = first[u]; e; e = nxt[e]) { int v = to[e]; if(v == fa) continue; if(f[v] != -1 && f[v] + w[e] == f[u]) h[v] = maxx; } } void dfs3(int u, int fa) { for(int e = first[u]; e; e = nxt[e]) { int v = to[e]; if(v == fa) continue; if(g[u] == -1) if(isg[u]) g[v] = w[e]; if(g[u] != -1) g[v] = max(g[v], g[u] + w[e]); if(h[v] != -1) g[v] = max(g[v], h[v] + w[e]); dfs3(v, u); } } signed main() { n = Read(), k = Read(); memset(h, -1, sizeof(h)); memset(g, -1, sizeof(g)); for(int i = 1; i < n; i++) { int x = Read(), y = Read(), z = Read(); Add(x, y, z), Add(y, x, z); } for(int i = 1; i <= k; i++) isg[Read()] = 1; dfs1(1, 0); ans[1] = fans[1]; dfs2(1, 0); dfs3(1, 0); for(int i = 1; i <= n; i++) printf("%lld\n", ans[i] - max(f[i], g[i])); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号