好题选讲(2)
[bzoj1426]收集邮票
Description
每次在$[1,n]$中等概率的选数,第$i$次选数需要付出$i$的代价,问选中所有数的期望代价。
$n\le10^4$
Sol
令$f_i$为选完$i$个数后期望取多少个数可以取完所有数,显然$f_n=0$。
考虑逆推,$f_i$有$\frac{i}{n}$的几率选到已有的,有$\frac{n-i}{n}$的几率选到没有的,那么我们有:
$$f_i=\frac{i}{n}f_i+\frac{n-i}{n}f_{i+1}$$
$$f_i=f_{i+1}+\frac{n}{n-i}$$
令$g_i$为选完$i$个数后期望付出多少代价来选到$n$。
那么$g_i$有$\frac{i}{n}$的概率转移到自己,后面的期望$f_i$次价格均加$1$,故需要加上$f_i$
剩下$\frac{n - i}{n}$的概率就只有后面的$f_{i+1}$次价格需要加$1$,那么我们有转移方程式:
$$g_i=\frac{i}{n}(g_i+f_i+1)+\frac{n-i}{n}(g_{i+1}+f_{i+1}+1)$$
化简可得$$g_i=\frac{n}{n-i}f_i+g_{i+1}$$
Code

#include<bits/stdc++.h> using namespace std; int Read() { int x = 0, f = 1; char ch = getchar(); while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();} while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();} return x * f; } int n; double f[10005], g[10005]; signed main() { n = Read(); for(int i = n - 1; i >= 0; i--) f[i] = f[i + 1] + 1.0 * n / (n - i); for(int i = n - 1; i >= 0; i--) g[i] = n * 1.0 / (n - i) * f[i] + g[i + 1]; printf("%.2lf\n", g[0]); return 0; }
[bzoj3450]Easy
Description
给你一个长为$n$的字符串,内含字符'o','x','?',定义这个字符串的得分为每一段连续的'o'字符的个数的平方之和,'?'有一半的概率是'o',求该字符串的期望得分。
$n\le 3\times 10^5$
Sol
平方的期望不好加,考虑消掉平方,观察到有$(x+1)^2=x^2+2x+1$,那么期望的个数就好算了。
令$f_i$为以$i$结尾的期望连续$0$个个数,那么我们有:
如果当前字符为'o',那么$f_i=f_{i-1}+1$,贡献为$2f_{i-1}+1$。
如果当前字符为'x',那么$f_i=0$,贡献为$0$。
如果当前字符为'?',那么$f_i$有一半的几率延续,故$f_i=\frac{f_{i-1}+1}{2}$,贡献为$\frac{2f_{i-1}+1}{2}$。
Code

#include<bits/stdc++.h> using namespace std; char ch[500005]; double f[500005], ans; int main() { int n; scanf("%d", &n); scanf("%s", ch + 1); for(int i = 1; i <= n; i++) { if(ch[i] == 'x') f[i] = 0; if(ch[i] == 'o') f[i] = f[i - 1] + 1, ans += 2 * f[i - 1] + 1; if(ch[i] == '?') ans += (2 * f[i - 1] + 1) / 2.0, f[i] = (f[i - 1] + 1) / 2.0; } printf("%.4lf\n", ans); }
[bzoj3029]守卫者的挑战
Description
有$n$个操作,给定数$l$,每个操作有$p_i$的概率成功,每次会将$l$加上$a_i$,求最终至少有$k$个操作成功且$l$的最终值非负的概率。
$n\le 200,l\le 2000, -1\le a_i\le10^3$
Sol
观察到$a_i$的和至多为$-200$,那么当正的$a_i$的和大于$200$时我们就可以令其为200,这样不会影响答案。
我们设$f_{i,j,k}$为进行了$i$轮比赛,赢了$j$轮,$a_i$和为$k$的概率,那么我们有:
$$f_{i+1,j-1,k+a_i} += f_{i,j,k}\times p_i$$
$$f_{i+1,j,k}+=f_{i,j,k}\times p_i$$
最后求出$\sum_{i=0}^{200}\sum_{j=l}^{n} f_{n,j,i}$
注意$a_i$可能为负,所以我们要右移一下,细节可以见代码。
Code

#include<bits/stdc++.h> using namespace std; int n, L, K, a[205]; double p[205], f[205][205][405]; int zh(int x) { if(x > n) x = n; return x + 201; } int main() { scanf("%d%d%d", &n, &L, &K); for(int i = 1; i <= n; i++) scanf("%lf", &p[i]), p[i] /= 100; for(int i = 1; i <= n; i++) scanf("%d", &a[i]); f[0][0][zh(K)] = 1.0; for(int i = 0; i < n; i++) for(int j = 0; j <= i; j++) for(int k = -i; k <= n; k++) { f[i + 1][j + 1][zh(k + a[i + 1])] += f[i][j][zh(k)] * p[i + 1]; f[i + 1][j][zh(k)] += f[i][j][zh(k)] * (1 - p[i + 1]); } double ans = 0; for(int i = L; i <= n; i++) for(int j = 0; j <= n; j++) ans += f[n][i][zh(j)]; printf("%.6lf\n", ans); }
[bzoj1419]Red is good
Description
Sol
首先看题目中提到的最优策略,它是指如果当前取一张牌的期望获得的钱小于$0$就停止。
那么我们定义$f_{i,j}$为考虑了$i$张红与$j$张黑时所能取到的期望收益(并不一定要取)
那么我们有方程式:
$$f_{i,j}=\frac{i}{i+j}*(f_{i-1,j}+1)+\frac{j}{i+j}*(f_{i,j-1}-1)$$
注意$f_{i,j}$可以不取,所以要与$0$取最大值
Code

#include<bits/stdc++.h> using namespace std; double f[2][5005]; int main() { int n, m; scanf("%d%d", &n, &m); for(int i = 0; i <= n; i++) { for(int j = 0; j <= m; j++) { f[i & 1][j] = max(0.0, (!i ? 0 : i * 1.0 / (i + j) * (f[(i & 1) ^ 1][j] + 1)) + (!j ? 0 : j * 1.0 / (i + j) * (f[i & 1][j - 1] - 1))); } } printf("%.6lf\n", f[n & 1][m] - 0.0000005); }
[bzoj3566]概率充电器
Description

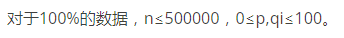
Sol
考虑两个由$100\%$导电的导线连接的点,一个点为$a\%$,一个点为$b\%$,那么第一个点通电的概率即为$1-(1-a)(1-b)$。
有了上述结果,我们就可以考虑一个点从自己子树以及从父节点传过来的概率。
要记住计算从父节点传过来的概率要减去其所在子树的概率。
Code

#include <bits/stdc++.h> using namespace std; int Read() { int x = 0, f = 1; char ch = getchar(); while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar(); } while (isdigit(ch)) { x = (x << 3) + (x << 1) + ch - '0'; ch = getchar(); } return x * f; } int first[1000005], nxt[1000005], to[1000005], w[1000005], tot = 0; int a[500005], dep[500005], num, n, m; double h[500005], ans = 0; void Add(int x, int y, int z) { nxt[++tot] = first[x]; first[x] = tot; to[tot] = y; w[tot] = z; } void dfs(int x) { for (int e = first[x]; e; e = nxt[e]) { int v = to[e]; if (!dep[v]) { dep[v] = dep[x] + 1; dfs(v); double k = h[v] * double(w[e]) / 100; h[x] = h[x] + k - h[x] * k; } } } bool check(double aa, double bb) { double eps = 1e-7; return ((aa - eps < bb) && (bb < aa + eps)); } void redfs(int x) { ans += h[x]; for (int e = first[x]; e; e = nxt[e]) { int v = to[e]; if (dep[v] > dep[x]) { if (check(h[v] * double(w[e]) / 100, 1)) { redfs(v); return; } double k = (h[x] - h[v] * double(w[e]) / 100) / (1 - h[v] * double(w[e]) / 100); k *= double(w[e]) / 100; h[v] = h[v] + k - h[v] * k; redfs(v); } } } int main() { n = Read(); for (int i = 1; i < n; i++) { int x = Read(), y = Read(), z = Read(); Add(x, y, z), Add(y, x, z); } for (int i = 1; i <= n; i++) { a[i] = Read(), h[i] = a[i] * 0.01; } dep[1] = 1; dfs(1), redfs(1); printf("%.6lf", ans); }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号