好题选讲(1)
[bzoj4300]绝世好题
Description
给定一个长为$n$的数列$a$,要求选出一个$a$的子集$b$,使得$b$的大小最大,且满足$b_i\space \&\space b_{i-1} ≠ 0$。
$n\le 10^5$
Sol
我们可以轻松得出一个$\mathcal{O}(n^2)$的DP方程式,令$f_i$表示以$i$结尾的最大子集的数的个数,那么我们有
$$f_i = \max\{f_j + 1\space |\space a_i \space\&\space a_j ≠ 0\}$$
我们考虑两个数进行与运算时的运算规则为,当两个数某位置上的数均为$1$时,答案的该位才为$1$。
所以我们令$f_i$表示满足运算后第$i$位总为$1$的子集的最大长度,还是根据和上面差不多的思路枚举即可。
时间复杂度$\mathcal{O}(n\log n)$
Code

#include<bits/stdc++.h>
using namespace std;
int f[35], n, a[100005];
int main() {
scanf("%d", &n); int ans = 0;
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
for(int i = 1; i <= n; i++) {
int k = 0;
for(int j = 0; j <= 30; j++)
if(a[i] & (1 << j)) k = max(k, f[j] + 1);
for(int j = 0; j <= 30; j++)
if(a[i] & (1 << j)) f[j] = k;
ans = max(ans, k);
}
cout << ans << endl;
}
[CF618F] Double Knapsack
Description
给定两个长为$n$的数组$a,b$,要求从$a,b$中个选出它们的一个子序列,使得两个子序列的总和相等。
$n\le 10^6, 0\le a_i,b_i\le 10^6$
Sol
不妨设$a$数组内所有数之和最大,那么我们可以记录$a,b$的前缀和$sa, sb$。
对于每个$i\in [0,n]$,我们枚举最小的$j\in [0,n]$且$sa_i-sb_j \in [0,n)$,这个可以用双指针来$\mathcal{O}(n)$实现。
当我们找到两个相同的$sa_i-sb_j$的值时,我们就可以取出它们之间的部分,那部分必定是相等的。
因为是$n+1$个数填入$n$个空内,所以根据鸽巢原理,必定至少有两个数为同一个值,所以一定有解。
时间复杂度$\mathcal{O}(n)$
Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
int Read() {
int x = 0, f = 1; char ch = getchar();
while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();}
return x * f;
}
int n, a[1000005], b[1000005], sa[1000005], sb[1000005];
struct mp {
int x, y;
}m[1000005];
signed main() {
n = Read();
for(int i = 1; i <= n; i++)
a[i] = Read(), sa[i] = sa[i - 1] + a[i];
for(int i = 1; i <= n; i++)
b[i] = Read(), sb[i] = sb[i - 1] + b[i];
for(int i = 0; i <= n; i++) m[i] = (mp){-1, -1};
bool rev = 0;
if(sa[n] < sb[n]) swap(sa, sb), rev = 1;
int i, v, pos = 0;
for(i = 0; i <= n; i++) {
while(sa[i] >= sb[pos + 1] && pos + 1 <= n) ++pos;
v = sa[i] - sb[pos];
if(m[v].x != -1) break;
m[v].x = i, m[v].y = pos;
}
if(rev) swap(i, pos), swap(m[v].x, m[v].y);
printf("%lld\n", i - m[v].x);
for(int j = m[v].x + 1; j <= i; j++) printf("%lld ", j);
puts("");
printf("%lld\n", pos - m[v].y);
for(int j = m[v].y + 1; j <= pos; j++) printf("%lld ", j);
return 0;
}
[bzoj2118]墨墨的等式
Description
给定长度为$n$的数列$a$,求$[l,r]$内所有满足方程$\sum_{i=1}^n a_ix_i=b$的所有解非负的$b$的个数。
$n\le 12,a_i\le5\times10^5,l,r\le 10^{12}$
Sol
观察到如果一组解为$\{x_1,x_2,...,x_n\}$,那么必有一组解$\{x_1+1,x_2,...,x_n\}$
所以我们令数列内最小的非零数为$minn$,那么我们只需要得出剩下的数组合起来对$minn$取模的余数有多少种与在取得该余数时最小是多少。
那么我们可以想到最短路,将每个余数看做一个点,并连向其能够加一次到达的点,跑最短路即可。
时间复杂度$\mathcal{O}(n\times \min\{a_i\}+kn)$
Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
int Read() {
int x = 0, f = 1; char ch = getchar();
while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();}
return x * f;
}
int first[6000005], nxt[6000005], to[6000005], w[6000005], tot = 0;
void Add(int x, int y, int z) {
nxt[++tot] = first[x];
first[x] = tot;
to[tot] = y;
w[tot] = z;
}
int n, l, r, len, a[55], minn = 1E9, dis[500005], inq[500005];
void spfa(int st) {
for(int i = 0; i < minn; i++) dis[i] = 1E18;
queue<int> q;
q.push(st);
dis[st] = 0;
inq[st] = 1;
while(!q.empty()) {
int u = q.front(); q.pop(); inq[u] = 0;
for(int e = first[u]; e; e = nxt[e])
if(dis[to[e]] > dis[u] + w[e]) {
dis[to[e]] = dis[u] + w[e];
if(!inq[to[e]]) q.push(to[e]), inq[to[e]] = 1;
}
}
}
int query(int x) {
int res = 0;
for(int i = 0; i < minn; i++)
if(dis[i] <= x) res += (x - dis[i]) / minn + 1;
return res;
}
signed main() {
n = Read(), l = Read(), r = Read();
for(int i = 1; i <= n; i++) {
a[i] = Read();
if(a[i]) a[++len] = a[i], minn = min(minn, a[i]);
}
sort(a + 1, a + len + 1);
n = len;
for(int j = 0; j < minn; j++)
for(int i = 1; i <= n; i++)
if(a[i] != minn)
Add(j, (j + a[i]) % minn, a[i]);
spfa(0);
printf("%lld\n", query(r) - query(l - 1));
return 0;
}
[bzoj3687]简单题
Description
给定长为$n$的数列$a$,求其所有子集算术和的异或和。
$n\le 1000,\sum a_i\le 2000000$
Sol
观察数据范围,容易想到应用bitset求子集类问题,如果一个值在bitset中的值为$1$,那么它对答案就有贡献。
初始化$b_0=1$
当插入一个数时,我们直接左移原bitset并与原bitset异或,最终查询扫一遍即可。
时间复杂度$\mathcal{O}(\frac{n^2}{32})$
Code

#include<bits/stdc++.h>
using namespace std;
int Read() {
int x = 0, f = 1; char ch = getchar();
while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();}
return x * f;
}
bitset<2000010> a;
signed main() {
int n, x;
scanf("%d", &n);
a[0] = 1;
for(int i = 1; i <= n; i++) {
scanf("%d", &x);
a ^= a << x;
}
int ans = 0;
for(int i = 1; i <= 2000000; i++) {
if(a[i]) ans ^= i;
}
printf("%d\n", ans);
return 0;
}
[bzoj1076]奖励关
Description

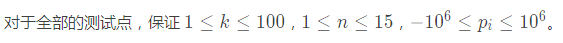
Sol
由于是期望问题,我们考虑逆推。
设$f_{i,j}$表示前$i-1$轮一共取到的宝物集合为$j$,从第$i$轮到第$k$轮的期望得分,答案即为$f_{1,0}$
那么我们可以枚举第$i$轮取哪些宝物,如果可以取,那么就分取与不取两种情况讨论,方程式为:
$$f_{i,j}+=\max\{f_{i+1,j},f_{i+1,j+2^l}\}$$
如果不能取,方程式就为:
$$f_{i,j}+=f_{i+1,j}$$
因为我们一共讨论了$n$种情况,那么期望值就要除以$n$。
时间复杂度$\mathcal{O}(kn2^n)$
Code

#include<bits/stdc++.h>
using namespace std;
int Read() {
int x = 0, f = 1; char ch = getchar();
while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)) {x = (x << 3) + (x << 1) + ch - '0'; ch = getchar();}
return x * f;
}
int n, k, qz[55], val[55];
double f[105][50005];
signed main() {
k = Read(), n = Read();
for(int i = 1; i <= n; i++) {
val[i] = Read();
int x;
while(x = Read()) qz[i] += 1 << (x - 1);
}
for(int i = k; i >= 1; i--) {
for(int j = 0; j < (1 << n); j++) {
for(int l = 1; l <= n; l++) {
if((j & qz[l]) == qz[l])
f[i][j] += max(f[i + 1][j], f[i + 1][j | (1 << (l - 1))] + val[l]);
else f[i][j] += f[i + 1][j];
}
f[i][j] /= n;
}
}
printf("%.6lf\n", f[1][0]);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号