一、 过拟合问题
1. 引入
线性回归当中：
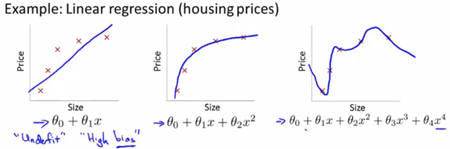
假设我们拿出房屋面积与房价的数据集，随着面积的增大，房价曲线趋于平缓。第一个模型不能很好地拟合，具有高偏差（欠拟合）。我们加入二次项后曲线可以较好的拟合，用第三个模型去拟合时，它通过了所有的数据点，但它是一条扭曲的线条，不停上下波动，我们并不认为它是一个预测房价的好模型。这个现象我们称为过度拟合。
（概括：过拟合现象常在变量过多的时候出现，能非常好的拟合训练数据，但无法泛化到新样本中。）
同样地，Logistic回归当中：
解决过拟合问题：
1) 减少特征数量
2) 正则化方法
二、正则化
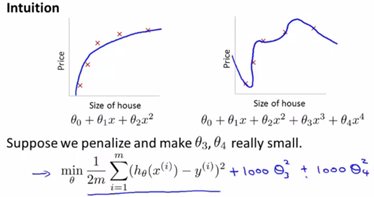
上图第二个模型不是一个好的拟合模型，现在我们在三次项和四次项上面加上惩罚项（penalize）如1000，我们要最小化这个新函数，就是 和 要尽可能小，他们会趋近于0，最后我们拟合得到的函数实际上是一个二次函数。总体来说我们在一些项上面加上惩罚项就相当于简化这个函数，使之更不容易出现过拟合的问题。
在实际问题中，如一个问题有100个参数，我们不知道该选择哪个它和标签相关度较低，此时我们修改代价函数来缩小所有的参数。
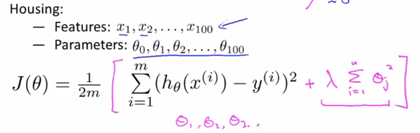
在代价函数中添加一个额外的正则化项，来缩小每个参数的值。
1. 线性回归的正则化
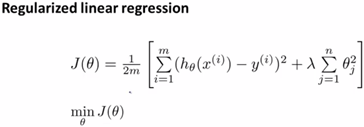
在usual linear regression基础上加上一个额外的正则化项，其中
是正则化参数，我们不需要对
一项进行正则化。
梯度下降法：
我们将与其他参数的更新过程分开，在此基础上求偏导数，这样就可以对正则化代价函数
使用梯度下降的方法进行最小化。
课堂记录：
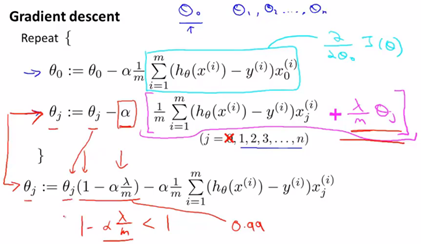
其中由于学习率很小，m很大，
是一个略小于1的数，举例可能是0.99，这一项乘上
相当于每次更新将
向0方向缩小一点点。
正规方程法：
这就是正则化后的正规方程法公式。
PS：关于矩阵不可逆问题，如果正则化参数
我们就可以保证括号中的矩阵一定是可逆的，因为正则化正好可以解决一些
不可逆的问题。
2. Logistic回归的正则化
加上一个额外的正则化项之后，即使我们有很多的特征和参数，也可以得到一个较好的拟合模型，避免过拟合现象。
代价函数和梯度：
代价函数增加了一个正则化项，梯度也随之相应改变。
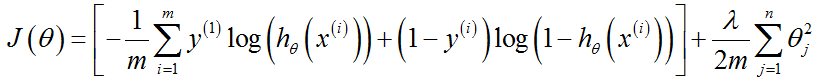
实现部分
下面是在上一篇笔记《Logistic回归模型实现》costFunction.m代码的基础啊上我们修改过后，正则化后的costFunctionReg.m
function [J, grad] = costFunctionReg(theta, X, y, lambda) %COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization m = length(y); % number of training examples J = 0; grad = zeros(size(theta)); % ============================================================= J = 1/m * (-y' * log(sigmoid(X*theta)) - (1 - y') * log(1 - sigmoid(X * theta))) + lambda/2/m*sum(theta(2:end).^2); grad(1,:) = 1/m * (X(:, 1)' * (sigmoid(X*theta) - y)); grad(2:size(theta), :) = 1/m * (X(:, 2:size(theta))' * (sigmoid(X*theta) - y))... + lambda/m*theta(2:size(theta), :); end
下面是lambda取值为【0,1,10,100】时的拟合结果，从结果可以看出，lambda = 0时，可能存在过拟合现象，lambda = 1/10时，获得较好模型。
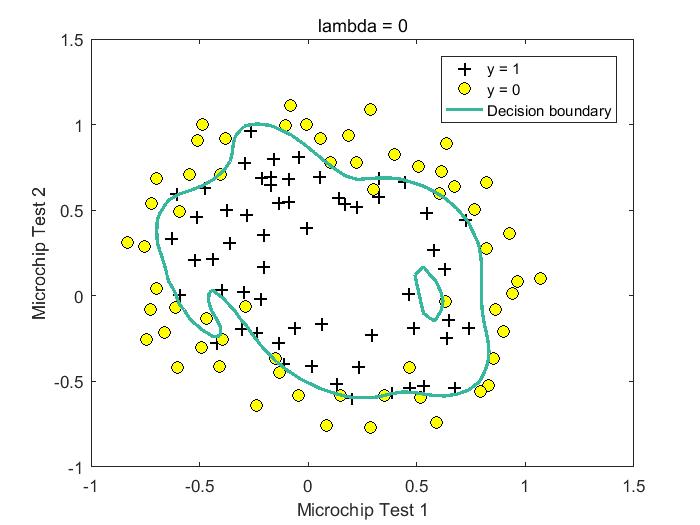
%lambda = 0 Train Accuracy: 87.288136
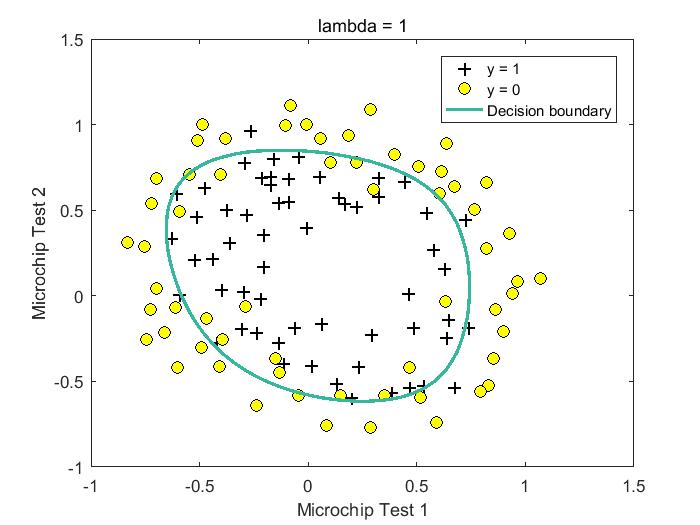
%lambda = 1 Train Accuracy: 83.050847 Expected accuracy (with lambda = 1): 83.1 (approx)
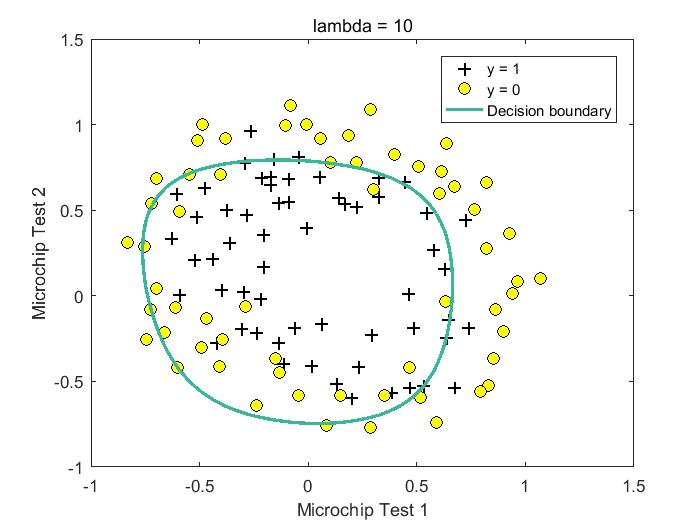
%lambda = 10 Train Accuracy: 83.050847
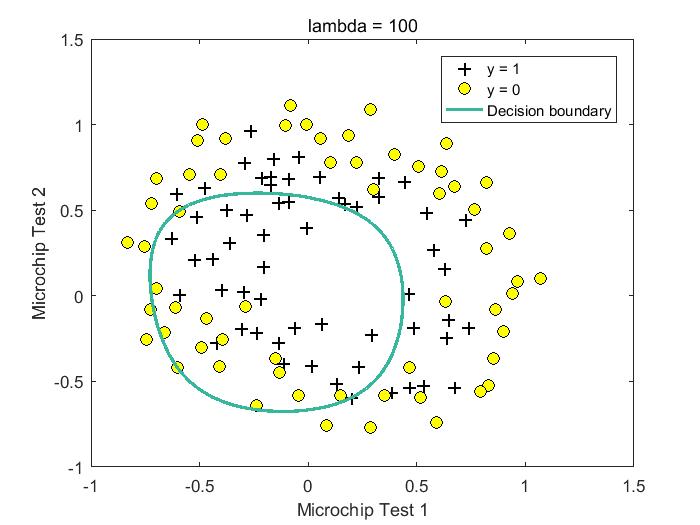
%lambda = 100 Train Accuracy: 61.016949
过程代码：
%% Machine Learning Online Class - Exercise 2: Logistic Regression %% Initialization clear ; close all; clc %% Load Data % The first two columns contains the X values and the third column % contains the label (y). data = load('ex2data2.txt'); X = data(:, [1, 2]); y = data(:, 3); plotData(X, y); hold on; xlabel('Microchip Test 1') ylabel('Microchip Test 2') % Specified in plot order legend('y = 1', 'y = 0') hold off; %% =========== Part 1: Regularized Logistic Regression ============ % Add Polynomial Features % Note that mapFeature also adds a column of ones for us, so the intercept % term is handled X = mapFeature(X(:,1), X(:,2)); % Initialize fitting parameters initial_theta = zeros(size(X, 2), 1); % Set regularization parameter lambda to 1 lambda = 100; % Compute and display initial cost and gradient for regularized logistic % regression [cost, grad] = costFunctionReg(initial_theta, X, y, lambda); fprintf('Cost at initial theta (zeros): %f\n', cost); fprintf('Expected cost (approx): 0.693\n'); fprintf('Gradient at initial theta (zeros) - first five values only:\n'); fprintf(' %f \n', grad(1:5)); fprintf('Expected gradients (approx) - first five values only:\n'); fprintf(' 0.0085\n 0.0188\n 0.0001\n 0.0503\n 0.0115\n'); fprintf('\nProgram paused. Press enter to continue.\n'); pause; % Compute and display cost and gradient % with all-ones theta and lambda = 10 test_theta = ones(size(X,2),1); [cost, grad] = costFunctionReg(test_theta, X, y, 10); fprintf('\nCost at test theta (with lambda = 10): %f\n', cost); fprintf('Expected cost (approx): 3.16\n'); fprintf('Gradient at test theta - first five values only:\n'); fprintf(' %f \n', grad(1:5)); fprintf('Expected gradients (approx) - first five values only:\n'); fprintf(' 0.3460\n 0.1614\n 0.1948\n 0.2269\n 0.0922\n'); fprintf('\nProgram paused. Press enter to continue.\n'); pause; %% ============= Part 2: Regularization and Accuracies ============= % Optional Exercise: % In this part, you will get to try different values of lambda and % see how regularization affects the decision coundart % % Try the following values of lambda (0, 1, 10, 100). % % How does the decision boundary change when you vary lambda? How does % the training set accuracy vary? % Initialize fitting parameters initial_theta = zeros(size(X, 2), 1); % Set regularization parameter lambda to 1 (you should vary this) lambda = 0; % Set Options options = optimset('GradObj', 'on', 'MaxIter', 400); % Optimize [theta, J, exit_flag] = ... fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options); % Plot Boundary plotDecisionBoundary(theta, X, y); hold on; title(sprintf('lambda = %g', lambda)) % Labels and Legend xlabel('Microchip Test 1') ylabel('Microchip Test 2') legend('y = 1', 'y = 0', 'Decision boundary') hold off; % Compute accuracy on our training set p = predict(theta, X); fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100); fprintf('Expected accuracy (with lambda = 0): (approx)\n');
