04-10大排序
十大经典排序算法
https://mp.weixin.qq.com/s/putWU_FBF7cZJkuVpCy0sw
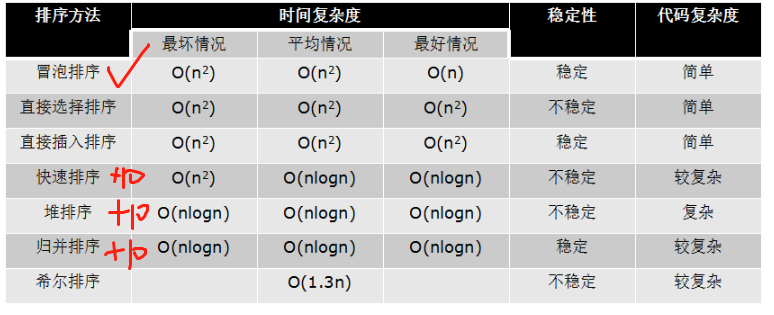


1.冒泡
def bubble_sort(data):
for i in range(len(data)-1):
exchange = False
for j in range(len(data)-i-1):
if data[j]>data[j+1]:
data[j],data[j+1]=data[j+1],data[j]
exchange=True
if not exchange: # 一趟没有交换,说明data是有序的
return data
return data
2.快排
def once_sort(data,left,right):
temp = data[left] # 选出第一个元素作为temp
while left<right:
while left<right and data[right]>temp:
right -=1
data[left]=data[right]
while left<right and data[left]<temp:
left+=1
data[right]=data[left]
data[left]=temp
return left
def quick_sort(data,left,right):
if left<right:
mid = once_sort(data,left,right)
data = quick_sort(data,left,mid-1) # temp左边排序
data = quick_sort(data,mid+1,right) # temp右边排序,不用管mid
return data
3.选择排序
li = [4,5,6,,7,8,9,9,54]
1、选择 li[0:n],最小下标为0,找出最小的元素,所对应的下标与0交换,交换值
2、选择 li[1:n], 最小下标为1,找出最小的元素,所对应的下标与1交换,交换值
3、反复
def select_sort(data):
for i in range(len(data)-1): # 当前N-1个数字排列好了,最后一个也就好了
min_index = i
for j in range(i+1,len(data)): # [1~n]
if data[j]<data[min_index]:
min_index = j # 最小下标交换
if min_index != i:
data[min_index],data[i]=data[i],data[min_index]
return data
4.插入排序
li = [43,34,354,342,21]
1、把第一个当做有序区,其他作为无序区
2、从[1:n]开始,选取temp=li[i], j =i-1
3、li[i],与li[i-1]比较 , 每次与前一个比较
4、若li[i]比temp大的话,li[i]向后移动1位
def insert_sort(data):
for i in range(1,len(data)):
temp = data[i] # 取出当前为未排序的数
j = i-1
while j>=0 and data[j]>temp: # 未排序的temp < 排序的数
data[j+1]=data[j] # 排序好的数,往后移一位
j -= 1
data[j+1] = temp # 未排序的temp > 排序的数,将temp插入到空出的位置
return data
5.希尔排序
分组插入排序
1、分组标准gap=len(data)//2,gap//=2
2、插入排序
3、gap替换1
def shell_sort(data):
gap = len(data)//2 # 取li长度的1/2
while gap>0:
# 插入排序 gap ---> 1
for i in range(gap,len(data)):
temp = data[i]
j = i-gap
while j >= 0 and data[j]>temp:
data[j+gap]=data[j]
j -= gap
data[j+gap] = temp
gap //= 2
return data
6.二路归并排序
二路归并
1. 先分解
将列表分解成一个个元素
2. 再合并
合并成 2段有序列表,列表越来越大
# merge
英 [mɜ:dʒ] 美 [mɜ:rdʒ]
融入;(使)混合;相融;渐渐消失在某物中
def merge(data,left,mid,right):
temp = []
i,j = left,mid+1
# 两段有序,[left~mid] [mid+1~right]
while i<=mid and j<=right:
if data[i]<data[j]:
temp.append(data[i])
i+=1
else:
temp.append(data[j])
j+=1
# 一段已经为空
while i<=mid: # i=mid也是要计算的
temp.append(data[i])
i+=1
while j<=right: # j=mid+1,没有=的话,就会漏掉mid
temp.append(data[j])
j+=1
# temp赋值给data[left:right]
data[left:right+1] = temp
return data
def merge_sort(data,left,right):
if left<right:
mid = (left+right)//2
# 分解
merge_sort(data,left,mid)
merge_sort(data,mid,right)
# 合并
merge(data,left,mid,right)
return data
7.堆排序
1.根据列表,构造堆,调整使堆有序
2.得到堆顶元素,为最大元素,去掉堆顶
3.将堆最后一个元素放到堆顶
4.调整使堆有序,堆顶元素为第二大元素
5.重复3
非线性排序:通过比较元素间的相对次序,复杂度不能突破O(nlogn)
线性排序:可以达到线性时间运行
8.计数排序
抽屉原理,统计每个数出现的次数
小范围:输入的数据必须是有确定范围的整数。
时间复杂度O(n+k) n个0~k之间的整数
空间复杂度O(n+k)
1.找出待排序数组的min,max
2.创建max+1长度的数组空间,元素初始化为0
3.统计重复元素出现的次数
4.对所有的计数累加
5.反向填充目标数组
9.桶排序
鸽巢排序,稳定
要求:data服从均匀分布
时间复杂度:当n=k时,达到O(n), O(n+k), 最坏O(n^2)
空间复杂度: O(n+k)
步骤:
1.设置一个定量的数组当作空桶;
2.遍历输入数据,并且把数据一个一个放到对应的桶里去;
3.对每个不是空的桶进行排序;
4.从不是空的桶里把排好序的数据拼接起来。
10.基数排序
时间复杂度:O(n*k) k为关键字
空间复杂度: O(n+k)
1.按照低位先排序,然后收集
2.按照高位排序,再收集
3,依次类推

 浙公网安备 33010602011771号
浙公网安备 33010602011771号