4- 算法练习leetcode.com

0、五大经典算法

动态规划算法----爬楼梯
分治算法--
贪心算法---零钱问题
回溯算法---迷宫问题 --深度优先
分支限界法 ----广度优先

　　

1、找出下标范围

 

1、二分法

li = [1,2,3,3,3,4,4,5]

def half_sort(data,value):
    low = 0
    high = len(li) -1
    while low<=high:
        mid = (low + high) // 2
        if data[mid] == value:
            return mid
        if data[mid] > value:
            # high = mid        # mid已经比较过了，可以舍弃掉
            high = mid -1
        if data[mid] < value:
            # low = mid
            low = mid + 1

index = half_sort(li,4)
print(index)

 2、错误版本

3、ok版本

def half_sort(data,value):
    low = 0
    high = len(li) -1
    while low<=high:
        mid = (low + high) // 2
        if data[mid] == value:
            left = mid
            right = mid
            while data[left] ==value and left>=0:       # 左边界
                left -= 1   
            while data[right] == value and right <= len(data):  # 右边界
                right += 1
            return (left+1, right-1)        # 稍微调整下标
        
        if data[mid] > value:
            high = mid -1
        if data[mid] < value:
            low = mid + 1
    return

li = [1,2,3,3,3,4,4,5]
index = half_sort(li,5)
print(index)

 

2、 返回两个数之和的下标

https://leetcode.com/problems/two-sum/?tab=Description

（1）双循环版本:O(n^2)

def findout(li, value):
    for i in range(len(li)):                # 1,2,5,4
        for j in range(i+1,len(li)):        #   2,5,4
            if li[i] + li[j] == value:
                return (i,j)

li = [1, 2, 5, 4]
ret = findout(li, 2)
print(ret)

 

 

　（2）二分法查找：O(nlogn)

li = [1, 2, 5, 4]
target = 5


def bin_search(data_set, val, low, high):
    while low <= high:
        mid = (low+high) //2
        if data_set[mid] == val:
            return mid
        elif data_set[mid] < val:
            low = mid +1
        else:
            high = mid -1
    return

def func2():
    import copy
    li2 = copy.deepcopy(li)     # [1, 2, 5, 4]
    li.sort()                   # [1, 2, 4, 5]
    for i in range(len(li)):
        a = i
        b = bin_search(li, target-li[a], i+1, len(li)-1)
        if b:
            # return (a,b)      # 返回的是排序后的li的下标 (0, 2)
            return (li2.index(li[a]), li2.index(li[b]))     # li.index(4)  # 求下标

print(func2())

 

 

 （3）建立下标list

# 建立下标list
li = [1, 2, 5, 4]
target = 5
max_num = 100

def func3():
    a = [ None for i in range(max_num+1)]
    for i in range(len(li)):
        a[li[i]] = i
        if a[target-li[i]] != None:
            return (a[li[i]],a[target-li[i]])

print(func3())

 

    

 

 　　（4）dict字典下标表示方式

 　　

 

3、递归练习1：斐波那契

# 方式1：list写法
def fib(n):
    li = []
    for i in range(n):
        if i == 0 or i ==1:
            li.append(1)
        else:
            li.append(li[i-2]+li[i-1])
    return li

print(fib(5))



# 方式2：while
def fib2(max):
    a, b = 0, 1
    count = 0
    while count < max:
        print(b, end=" ")
        b, a = a+b, b
        count += 1
fib2(5)




# 方式3:yield
def fib2(max):
    a, b = 0, 1
    count = 0
    while count < max:
        yield b
        b, a = a+b, b
        count += 1

for item in fib2(5):
    print(item,end=" ")

 

# 牛逼版本
def fib(n):
    if n<=1 :
        return 1
    else:
        return fib(n-2) + fib(n-1)

print([fib(n) for n in range(10)])

 

 

# 装饰器版本

# 装饰器版本
def cache(func):
    cache = {}
    def wrap(*args):
        if args not in cache:
            cache[args] = func(*args)
        return cache[args]
    return wrap


@cache
def fib(n):
    if n<=1 :
        return 1
    else:
        return fib(n-2) + fib(n-1)

print([fib(n) for n in range(10)])

 

4、递归问题-爬楼梯

假设你正在爬楼梯，需要n步你才能到达顶部。但每次你只能爬一步或者两步，你能有多少种不同的方法爬到楼顶部？

您在真实的面试中是否遇到过这个题？ yes

比如n=3，1+1+1=1+2=2+1=3，共有3中不同的方法

返回 3

 

题目分析：

**设f(n)为n阶台阶的情况下，所有不同的跳法方法的总和！**
1.如果起始跳一阶的话，剩余的n-1阶就有 f(n-1) 种跳法；
2.如果起始跳二阶的话，剩余的n-2阶就有 f(n-2) 种跳法；
所以f(n) = f(n-1) + f(n-2)，实际结果即为斐波纳契数。

def fib(n):
    if n<=1 :
        return 1
    else:
        return fib(n-2) + fib(n-1)

print(fib(3))

 

 

一次性走1步，2步，3步？？？是否正确

def climb(n,steps):
    count = 0
    if n<=1:
        count = 1
    else:
        for step in steps:
            count += climb(n-step, steps)
    return count

print(climb(3,(1,2,3)))  # 一次性走 1,2,3

 

def fib(n):
    if n<=1 :
        return 1
    else:
        return fib(n-2) + fib(n -1) + fib(n-3)  # 一次性走 1,2,3 
print(fib(3))

 

5、递归练习2：汉诺塔问题

　　汉诺（Hanoi）塔问题：古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小不等，大的在下，小的在上（如图）。
有一个和尚想把这64个盘子从A座移到B座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。
在移动过程中可以利用B座，要求打印移动的步骤。如果只有一个盘子，则不需要利用B座，直接将盘子从A移动到C。

 

解决思路：

我们可以倒着想： 
也就是说，

　　当有n个时，由于游戏规则，最终必定将第n块由A搬到C，因为这一块最大，无法进行中转；

　　同时，当移动n时，A塔只有n，C塔空，则B塔有1~n-1，且按唯一顺序（由小到大）排列。 

接下来的问题是：

　　1~n-1是怎么从A到B的？此时将B看作目标塔，C作为辅助塔。这个问题就变成了n-1时的情况。。 
　　接着刨下去，我们就能够得到仅需解决n=1的情况，由此解决1~n-1运到B的问题

 

然后别忘了还要把这n-1块从B借A搬到C。而这不过是上述问题把初始塔和辅助塔互换而已。

 

 

假设有n个盘子：

• 1.把n-1个圆盘从A经过C移动到B
• 2.把第n个圆盘从A移动到C
• 3.把n-1个小圆盘从B经过A移动到C

 总结：汉诺塔移动次数的递推式：h(x)=2h(x-1)+1

     

　　　　

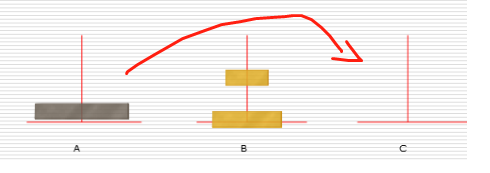
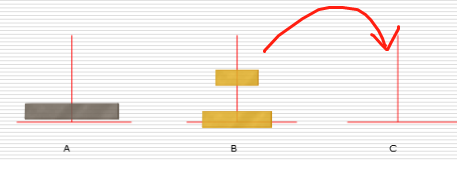
 代码实现

def hanno(n,a,b,c):
    if n ==1 :
        move(a,c)
    else:
        hanno(n-1,a,c,b)        #  将n-1个盘子从a经过c移动到b
        move(a,c)               # 将剩余的最后一个盘子从a移动到c
        hanno(n-1,b,a,c)        #  #将n-1个盘子从b经过a移动到c
def move(a,c):
    print(a,'-->',c)

hanno(3,'柱子A','柱子B','柱子C')

 

  

6、贪心算法：零钱

     所谓贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。

 

找零问题：假设商店老板需要找零n元钱，钱币的面额有：100元、50元、20元、5元、1元，如何找零使得所需钱币的数量最少？

def change_money(x):
    money = [100, 50, 20, 5, 1]
    change = [0,0,0,0,0]

    for index,item in enumerate(money):
        change[index] = x //money[index]
        x = x % money[index]        # 总钱数除 100 取余 56
    if x>0:
        print('还剩下',x)
    return change

print(change_money(456))

 

1.找零钱问题:假设只有1分、2分、五分、1角、二角、五角、1元的硬币。
在超市结账时,如果需要找零钱,收银员希望将最少的硬币数找给顾客。
那么,给定需要找的零钱数目,如何求得最少的硬币数呢

def change_money2(x):
    money =  [1, 0.5, 0.2, 0.1, 0.05, 0.02, 0.01]
    change = [0,   0,    0,   0,  0,  0, 0]
    for index,item in enumerate(money):
        change[index] = x // money[index]
        x = x % money[index]
    if x > 0 :
        print('还剩下',x)
    new_change = dict(zip(money,change))        # zip拉链
    return new_change

print(change_money2(12.125))