2-2 浮点数

 

1.浮点型

 

Python的浮点数就是数学中的小数(alex一定要强调float是有限小数或无限循环小数，就好像谁真的关心似的)。

在运算中，整数与浮点数运算的结果也是一个浮点数。

 

 

2.为什么要叫做float浮点型？

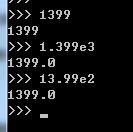
浮点数也就是小数，之所以称为浮点数，是因为按照科学记数法表示时，
一个浮点数的小数点位置是可变的，比如，
1.23*109和12.3*108是相等的。
浮点数可以用数学写法，如1.23，3.14，-9.01，等等。但是对于很大或很小的浮点数，就必须用科学计数法表示，把10用e替代：
1.23*109就是1.23e9，或者12.3e8，0.000012可以写成1.2e-5，等等。
整数和浮点数在计算机内部存储的方式是不同的，整数运算永远是精确的而浮点数运算则可能会有四舍五入的误差。

 　　

 

 

3.科学计数法

 

 

4.复数

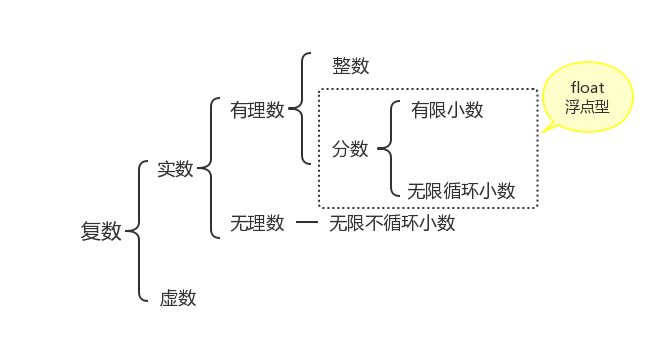
从上面的图中我们就可以看出，复数complex是由实数和虚数组成的

要了解复数，其实关于复数还需要先了解虚数。虚数(就是虚假不实的数):平方为复数的数叫做虚数。

复数是指能写成如下形式的数a+bi，这里a和b是实数，i是虚数单位(即-1开根)。在复数a+bi中，a称为复数的实部，b称为复数的虚部(虚数是指平方为负数的数)，i称为虚数单位。

当虚部等于零时，这个复数就是实数；当虚部不等于零时，这个复数称为虚数。

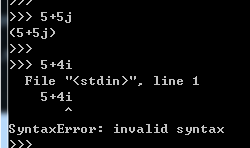
注，虚数部分的字母j大小写都可以。

 　　

 

 5.浮点精确度问题

Python默认的是17位精度,也就是小数点后16位，尽管有16位，但是这个精确度却是越往后越不准的。

首先，这个问题不是只存在在python中，其他语言也有同样的问题

>>> a = 3.141592653513651054608317828332
>>> a
3.141592653513651

 

 

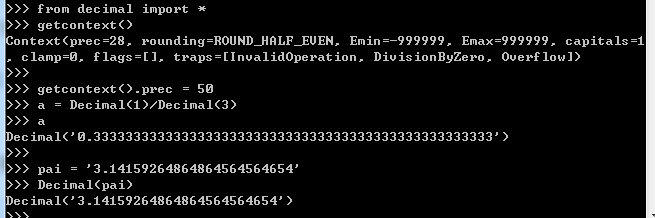
 这里有一个问题，就是当我们的计算需要使用更高的精度（超过16位小数）的时候该怎么做呢？

#借助decimal模块的“getcontext“和“Decimal“ 方法
>>> a = 3.141592653513651054608317828332
>>> a
3.141592653513651
>>> from decimal import *
>>> getcontext()
Context(prec=50, rounding=ROUND_HALF_EVEN, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[FloatOperation], traps=[InvalidOperation, DivisionByZero, Overflow])
>>> getcontext().prec = 50
>>> a = Decimal(1)／Decimal(3)#注，在分数计算中结果正确，如果直接定义超长精度小数会不准确
>>> a
Decimal('0.33333333333333333333333333333333333333333333333333')

>>> a = '3.141592653513651054608317828332'
>>> Decimal(a)
Decimal('3.141592653513651054608317828332')

 

　　

 

 

#不推荐：字符串格式化方式，可以显示，但是计算和直接定义都不准确，后面的数字没有意义。
>>> a = ("%.30f" % (1.0/3))  
>>> a  
'0.333333333333333314829616256247'