Leetcode 88. 合并两个有序数组 Python题解
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/merge-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
1.暴力法
解题思路:由于题目要求原地合并,直接返回nums1数组。因此一个可行的方案是合并两个列表,然后对合并后的列表进行排序。
用到的知识:
-
列表切片:如果要将一个列表A完整地赋值给另一个列表切片
B[k:],则直接将A作为右值即可,即B[k:]=A,无需将A作为切片表示。 -
列表排序之sort()方法
用法:nums.sort(reverse=False)
含义:在列表nums上原地排序,不需要赋值,nums已经有序。默认reverse=False,即升序。令reverse=True,得到降序后的列表。也可以自定义函数,控制升序或降序。
特点:仅作用于列表 -
排序之sorted方法
用法:nums=sorted(nums, reverse=False)
含义:对列表nums排序,返回排序后的新列表,因此需要赋值,否则nums仍然无序。默认reverse=False,即升序。令reverse=True,得到降序后的列表。
特点:可作用于所有可迭代对象 -
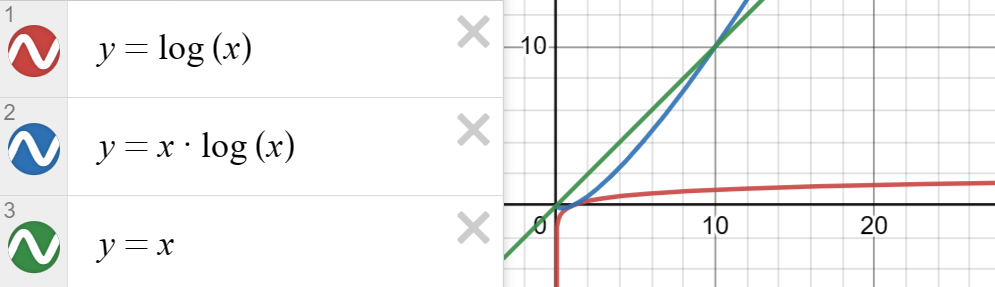
x、log(x)、x*log(x)的比较
提交代码:
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
nums1[m:]=nums2
nums1.sort()
复杂度分析:
等于快排的时间复杂度和空间复杂度
- 时间复杂度:(m+n)log(m+n)
- 空间复杂度:O(log(m+n))
切片赋值的时间复杂度是o(m+n)吗?如果是的话,O(log(m+n))应该小于o(m+n),则此时的空间复杂度不应该是o(m+n)吗?
2.逆向双指针
解题思路:从前往后比较的双指针方法需要移动大量的元素,由于题目给出的数组大小等于合并后的大小,如果比较方向转换为从后往前,插入两个列表中的较大值,则不需要额外的空间,时间复杂度也能够降低。
提交代码:
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
L1=m-1
L2=n-1
tail=m+n-1
while L1>=0 and L2>=0:
if nums1[L1]>nums2[L2]:
nums1[tail]=nums1[L1]
L1-=1
else:
nums1[tail]=nums2[L2]
L2-=1
tail-=1
if L2>=0:
nums1[0:tail+1]=nums2[0:L2+1]
复杂度分析:
- 时间复杂度:O(m+n)
- 空间复杂度:O(1)
3.题目描述
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。合并结果是 [1,2,2,3,5,6]。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。合并结果是 [1]。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。合并结果是 [1] 。
注意:因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-109 <= nums1[i], nums2[j] <= 109



