AGC001 D-F

AGC001D

题意：给你一个数列 $a$，你需要构造一个数列 $b$，使得同时满足这两个条件的数列只能所有元素相等：
1、前 $a_1$ 个数回文，接着 $a_2$ 个数回文，再接着 $a_3$ 个数回文……
2、前 $b_1$ 个数回文，接着 $b_2$ 个数回文，再接着 $b_3$ 个数回文……
无解输出 Impossible。
题解：
1、对于开头的一段，有下面两种情况（红色表示数列 $a$ 的限制，绿色表示数列 $b$ 的限制，后同）：

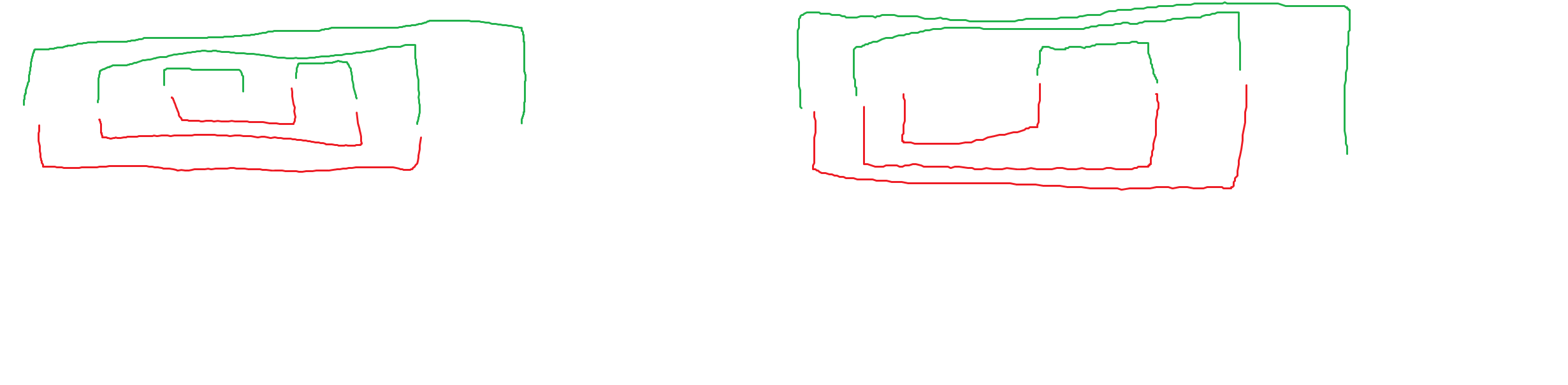
2、对于中间的一段，有下面一种情况：

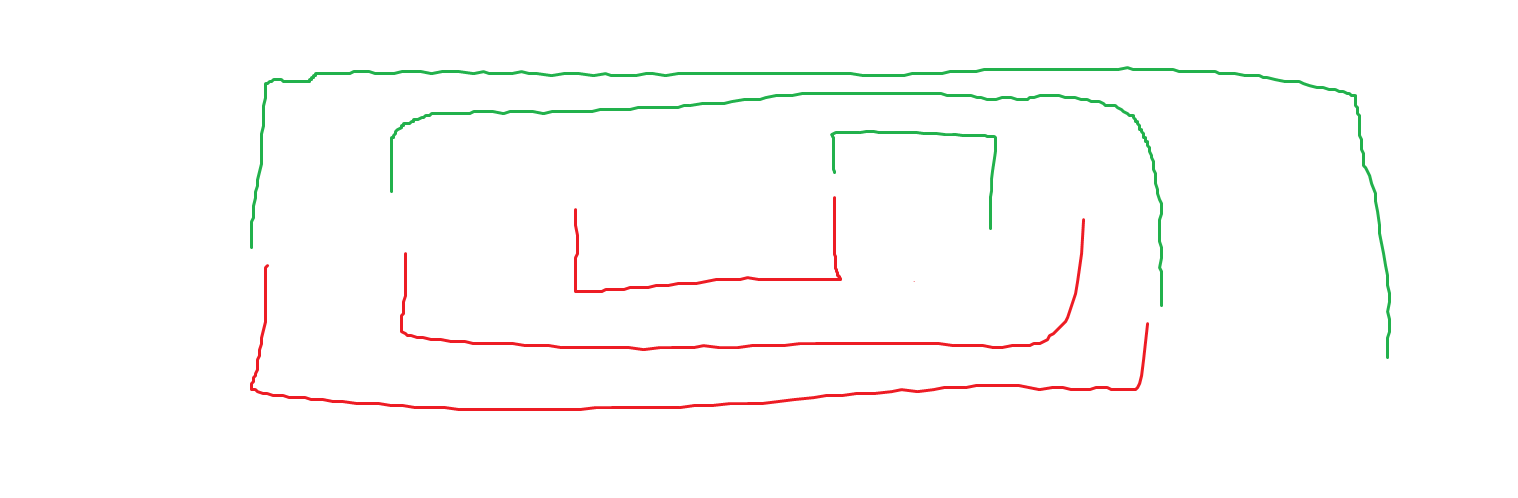
3、对于最后的一段，与开头的情况对称，懒得画了。

根据图很容易发现，只有开头和结尾的 $a$ 可能为奇数，奇数超过两个就无解，在以内就丢首尾就行了。

$b$ 根据图就是开头比 $a$ 多 $1$，结尾比 $a$ 少 $1$，中间一样的，注意特判 $a$ 长度为 $1$ 和 $b$ 的最后一位为 $0$。

AGC001E

题意：求

$$\sum_{i=1}^{n}\sum_{j=i+1}^{n}{a_i+b_i+a_j+b_j \choose a_i+a_j}$$

题解：考虑 ${a+b \choose a}$ 是从 $(0,0)$ 走到 $(a,b)$ 且每一步只能往上或往右走一个单位长度的方案数。

显然这题就是让我们求所有从 $(0,0)$ 走到 $(a_i+a_j,b_i+b_j)$ 的方案数，显然我们可以考虑平移，因为平移这个矩形以后大小不变，所以答案也不变。

那我们可以平移成求所有从 $(-a_i,-b_i)$ 走到 $(a_j,b_j)$ 的方案数的和，但是如果直接算复杂度是和暴力没有区别的，所以我们考虑设 $dp[i][j]$ 为所有的 $(-a_i,-b_i)$ 走到 $(i,j)$ 的方案数的和，因为答案要求从 $i+1$ 开始，所以要减去所有的 ${2a_i+2b_i \choose 2a_i}$ ，然后将答案除以 $2$ 即可。

AGC001F

题意：给一个 $1$ ~ $n$ 的排列 $p$ 和一个数 $k$，两个数 $p_i$、$p_j$ 可以交换当且仅当 $|i-j|\ge k$ 且 $|p_i-p_j|=1$，求交换后字典序最小的排列。

题解：考虑 $p$ 的逆置换 $q$，然后发现对于 $|q_i-q_j|<k$ 的两个位置 $i$、$j$，这两个位置上的值不可能被交换，也就是他们的相对位置是固定的。

还原到 $p$，也就是对于 $|i-j|<k$ ，两个位置的大小关系是不变的，从小到大建个DAG，然后就是求给这个DAG编号后，最小的拓扑排序的序列。

我们建反图，跑拓扑，然后按照 $N$ ~ $1$ 标号，显然不可能真的建图，复杂度爆炸，我们考虑线段树（树状数组也行）维护这个图，发现用线段树存进所有 $p$ 以后，$p_i$ 的值等于 $(i-k,i+k)$ 之间的最大值时，度数为 $0$，用一个堆装这些度数为 $0$ 的点，删掉以后就设为 $-\infty$，一直这样直到每个点都被删掉就做完了。

__EOF__

本文作者：Foraino0267
本文链接：https://www.cnblogs.com/vegtable-foraino/p/16204177.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！