AES加密算法原理(加密过程)
Rijndael(读作rain-dahl)是由美国国家标准与技术协会(NIST)所选的高级加密标准(AES)的候选算法。
AES算法流程:
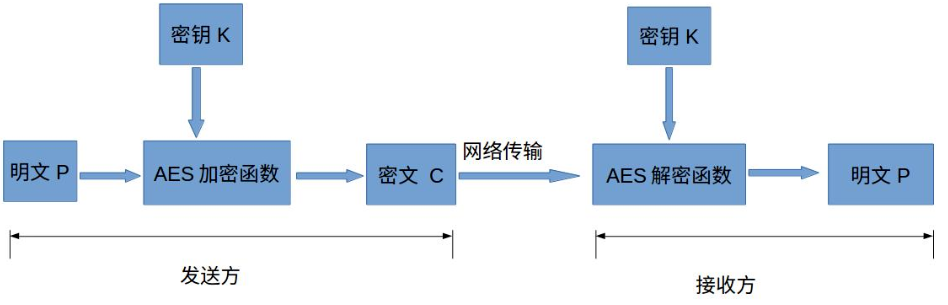
下面简单介绍下各个部分的作用与意义:
- 明文P:
没有经过加密的数据。
- 密钥K:
用来加密明文的密码,在对称加密算法中,加密与解密的密钥是相同的。密钥为接收方与发送方协商产生,但不可以直接在网络上传输,否则会导致密钥泄漏,通常是通过非对称加密算法加密密钥,然后再通过网络传输给对方,或者直接面对面商量密钥。密钥是绝对不可以泄漏的,否则会被攻击者还原密文,窃取机密数据。
- AES加密函数:
设AES加密函数为E,则 C = E(K, P),其中P为明文,K为密钥,C为密文。也就是说,把明文P和密钥K作为加密函数的参数输入,则加密函数E会输出密文C。
- 密文C:
经加密函数处理后的数据
- AES解密函数:
设AES解密函数为D,则 P = D(K, C),其中C为密文,K为密钥,P为明文。也就是说,把密文C和密钥K作为解密函数的参数输入,则解密函数会输出明文P。
在这里简单介绍下对称加密算法与非对称加密算法的区别。
- 对称加密算法:
加密和解密用到的密钥是相同的,这种加密方式加密速度非常快,适合经常发送数据的场合。缺点是密钥的传输比较麻烦。
- 非对称加密算法:
加密和解密用的密钥是不同的,这种加密方式是用数学上的难解问题构造的,通常加密解密的速度比较慢,适合偶尔发送数据的场合。优点是密钥传输方便。常见的非对称加密算法为RSA、ECC和EIGamal。
实际中,一般是通过RSA加密AES的密钥,传输到接收方,接收方解密得到AES密钥,然后发送方和接收方用AES密钥来通信。
AES算法流程:
AES加密过程涉及到4种操作,分别是字节替代、行移位、列混淆和轮密钥加。解密过程分别为对应的逆操作。由于每一步操作都是可逆的,按照相反的顺序进行解密即可恢复明文。加解密中每轮的密钥分别由初始密钥扩展得到。算法中16个字节的明文、密文和轮密钥都以一个4x4的矩阵表示。
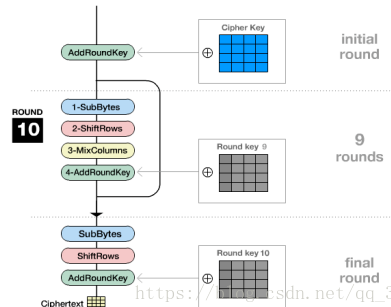
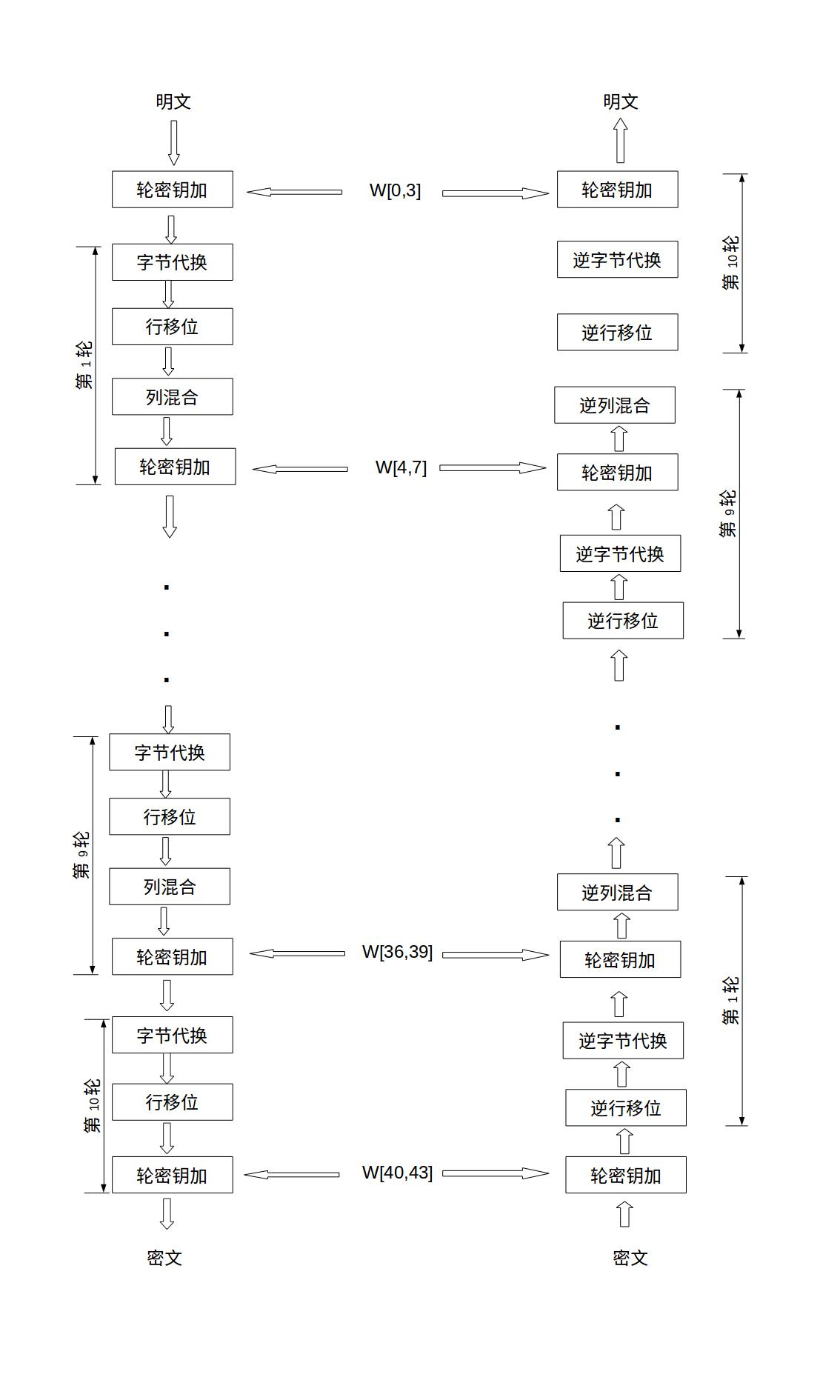
一、字节代换
1.字节代换操作
AES的字节代换其实就是一个简单的查表操作。AES定义了一个S盒和一个逆S盒。
AES的S盒:
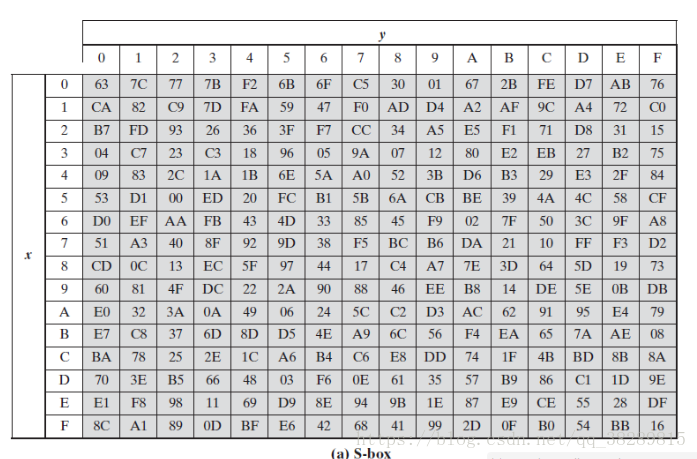
2.字节代换逆操作
逆字节代换也就是查逆S盒来变换,逆S盒如下:
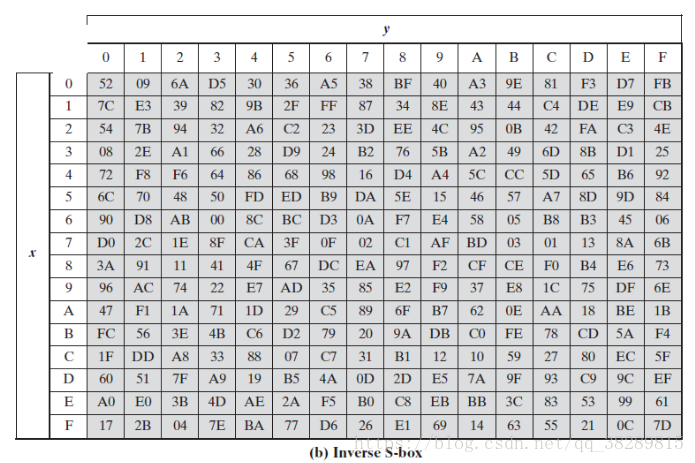
举例:字节66替换后的值为S[6][6]=33,再通过S-1即可得到替换前的值,S-1[3][3]=66。
二、行位移
1.行移位:行移位的功能是实现一个4x4矩阵内部字节之间的置换。
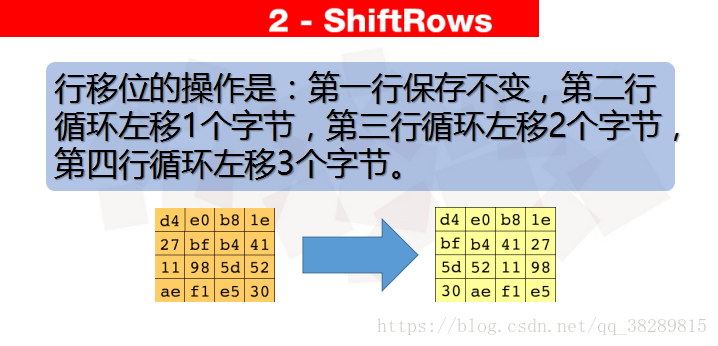
三、列混淆
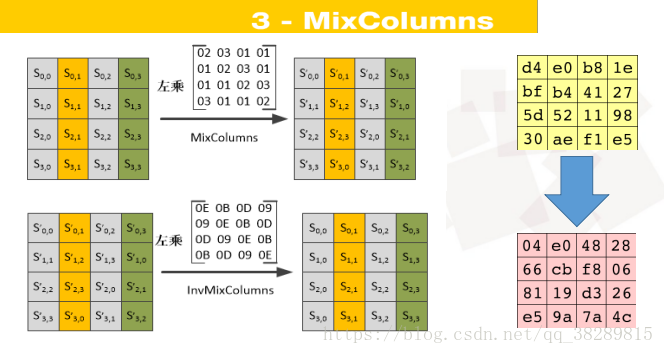
根据矩阵的乘法可知,在列混淆(利用域GF(28)上的算术特性的一个代替)的过程中,每个字节对应的值只与该列的4个值有关系。此处的乘法和加法需要注意如下几点:
(1)将某个字节所对应的值乘以2,其结果就是将该值的二进制位左移一位,如果该值的最高位为1(表示该数值不小于128),则还需要将移位后的结果异或00011011
(2)乘法对加法满足分配率,例如:07·S0,0=(01⊕02⊕04)·S0,0= S0,0⊕(02·S0,0)(04·S0,0)
(3)此处的矩阵乘法与一般意义上矩阵的乘法有所不同,各个值在相加时使用的是模2加法(异或运算)。
因为:说明两个矩阵互逆,经过一次逆向列混淆后即可恢复原文。
补充:(按位异或的概念)

4.轮密钥加:加密过程中,每轮的输入与轮密钥异或一次(当前分组和扩展密钥的一部分进行按位异或);因为二进制数连续异或一个数结果是不变的,所以在解密时再异或上该轮的密钥即可恢复输入。首尾使用轮密钥加的理由:若将其他不需要密钥的阶段放在首尾,在不用密钥的情况下就能完成逆过程,这就降低了算法的安全性。
加密原理:轮密钥加本身不难被破解,另外三个阶段分别提供了混淆和非线性功能。可是字节替换、行移位、列混淆阶段没有涉及密钥,就它们自身而言,并没有提供算法的安全性。但该算法经历一个分组的异或加密(轮密钥加),再对该分组混淆扩散(其他三个阶段),再接着又是异或加密,如此交替进行,这种方式非常有效非常安全。
5.密钥扩展:其复杂性是确保算法安全性的重要部分。当分组长度和密钥长度都是128位时,AES的加密算法共迭代10轮,需要10个子密钥。AES的密钥扩展的目的是将输入的128位密钥扩展成11个128位的子密钥。AES的密钥扩展算法是以字为一个基本单位(一个字为4个字节),刚好是密钥矩阵的一列。因此4个字(128位)密钥需要扩展成11个子密钥,共44个字。
密钥扩展过程说明:将初始密钥以列为主,转化为4个32 bits的字,分别记为w[0…3];按照如下方式,依次求解w[i],其中i是整数并且属于[4,43]。
1)将w[i]循环左移一个字节。
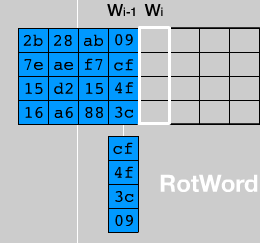
2)分别对每个字节按S盒进行映射。
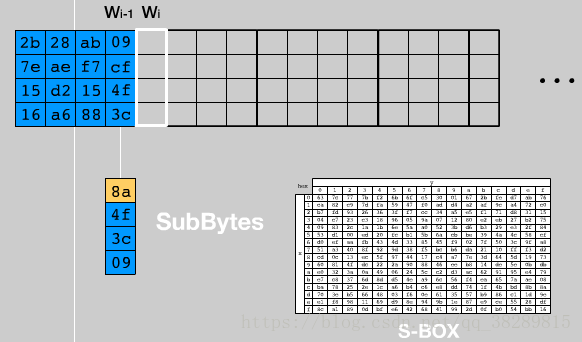
3)32 bits的常量(RC[i/4],0,0,0)进行异或,RC是一个一维数组,其中RC = {01, 02, 04, 08, 10, 20, 40, 80, 1B, 36}。

4)除了轮密钥的第一列使用上述方法,之后的二到四列都是w[i]=w[i-4]⊕w[i-1]
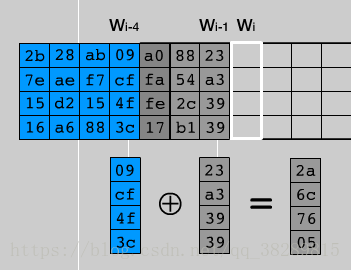
5)最终得到的第一个扩展密钥为(之后的每一轮密钥都是在前一轮的基础上按照上述方法得到的):
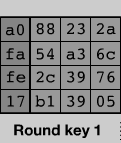
参考原文链接:
https://blog.csdn.net/qq_38289815/article/details/80900813 (AES)
https://blog.csdn.net/qq_28205153/article/details/55798628 (AES)
https://zhidao.baidu.com/question/318582446.html (按位异或的概念)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号