【线性代数的本质】以线性变换的眼光看待叉积
叉积
@
叉积的标准解释
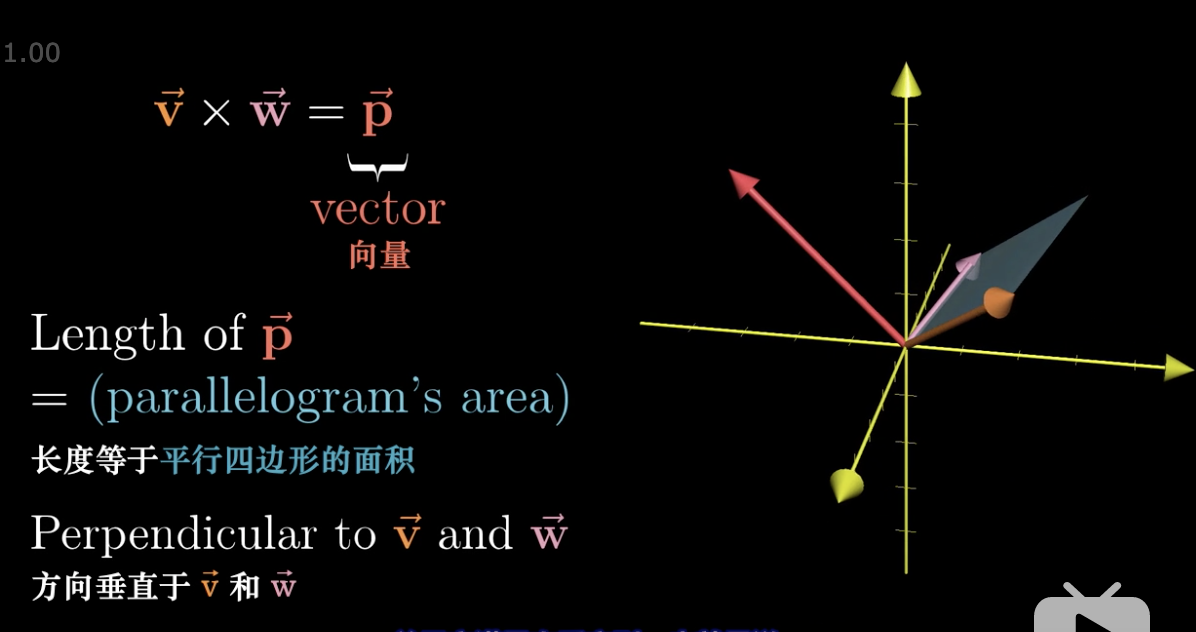
如果我们有两个向量，我们以这两个向量为边做一个平行四边形，这个平行四边形的面积就是这两个向量叉积的结果。
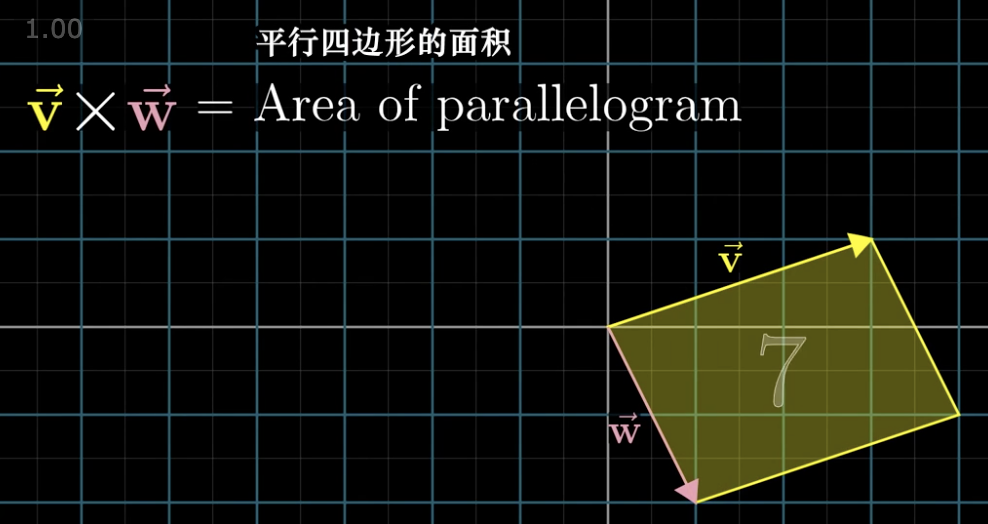
但是我们还是需要考虑定向问题，其实就是 i 和 j 向量的顺序，如果 j 在 i 的逆时针方向，那么就称为正的，否则为负的。
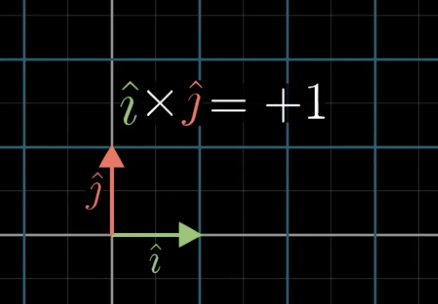
然后我们就可以计算出这个叉积的结果：
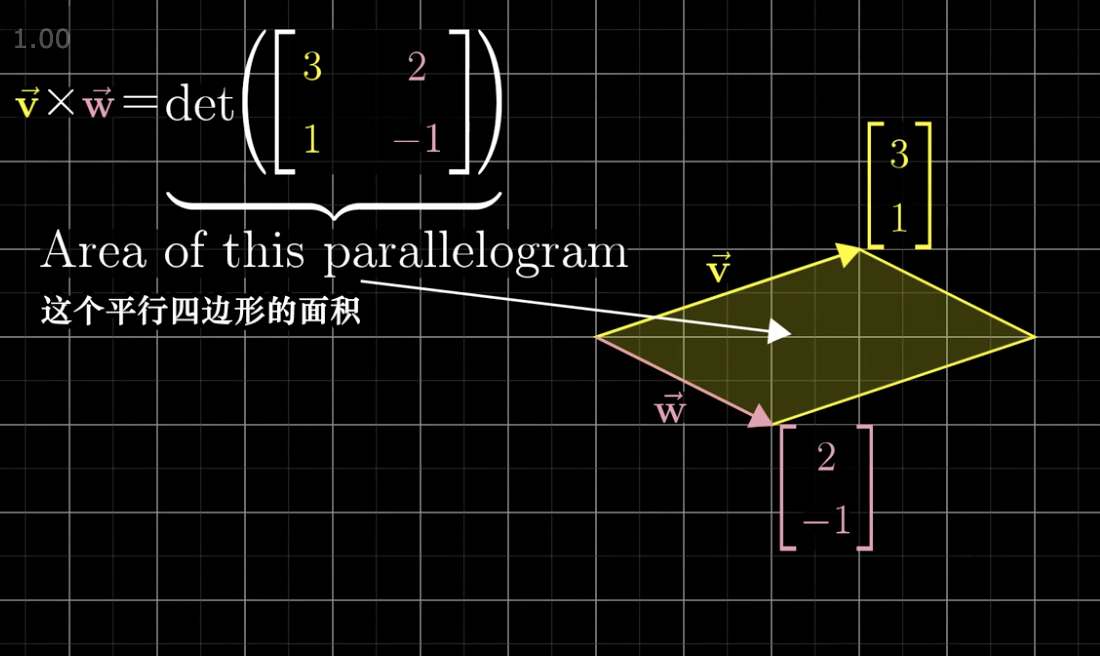
严格意义意义上说，以下三维向量才是叉积的定义（这里写成了列向量的形式，但是不会改变行列式的值，因为转置不改变行列式的值）
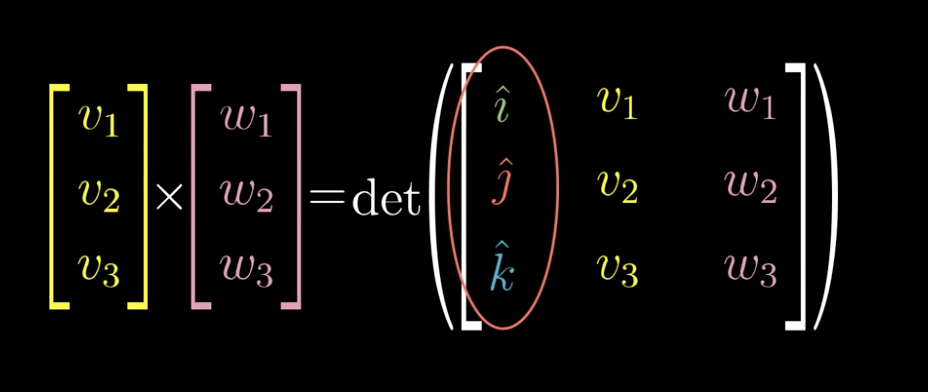
从线性变换看待叉积
为什么叉积是这种形式呢？
我们可以通过计算出这些内容，但是我们来介绍一个更好的推理过程。
- 我们将定义一个从三维空间到数轴的特定线性变换，并且它是根据
v和w来定义的。 - 找到他的对偶向量
- 这个对偶向量就会是
v和w的叉积。
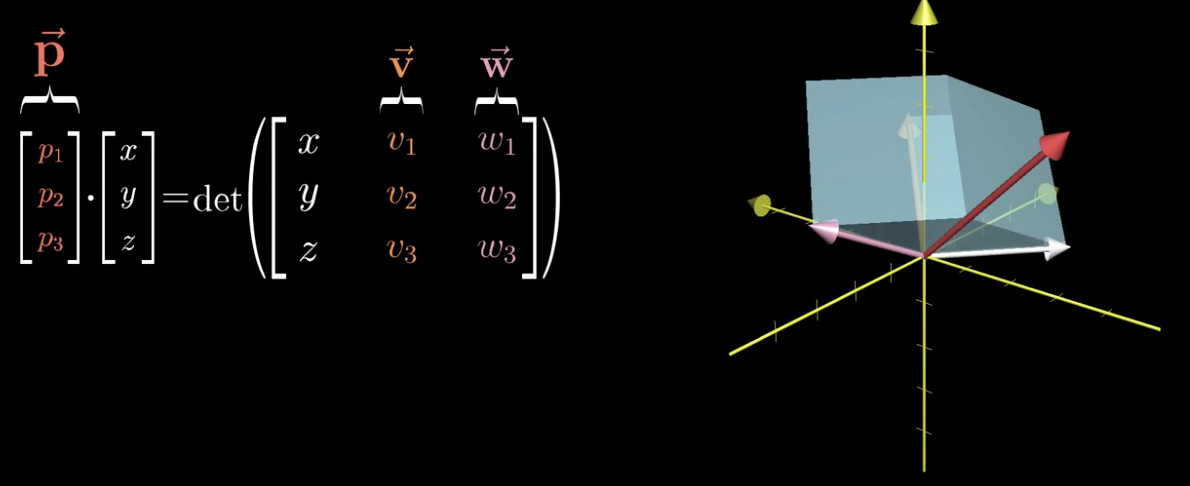
其实就相当于转化为下面这个问题的答案？
Q：当你将向量 p 和某个向量（x，y，z）点乘的时候，所得的结果等于一个 3x3 矩阵的行列式，这个矩阵第一行为（x，y，z），其余两列为 v 和 w 的坐标，要找到一个向量 p 满足上述行为。
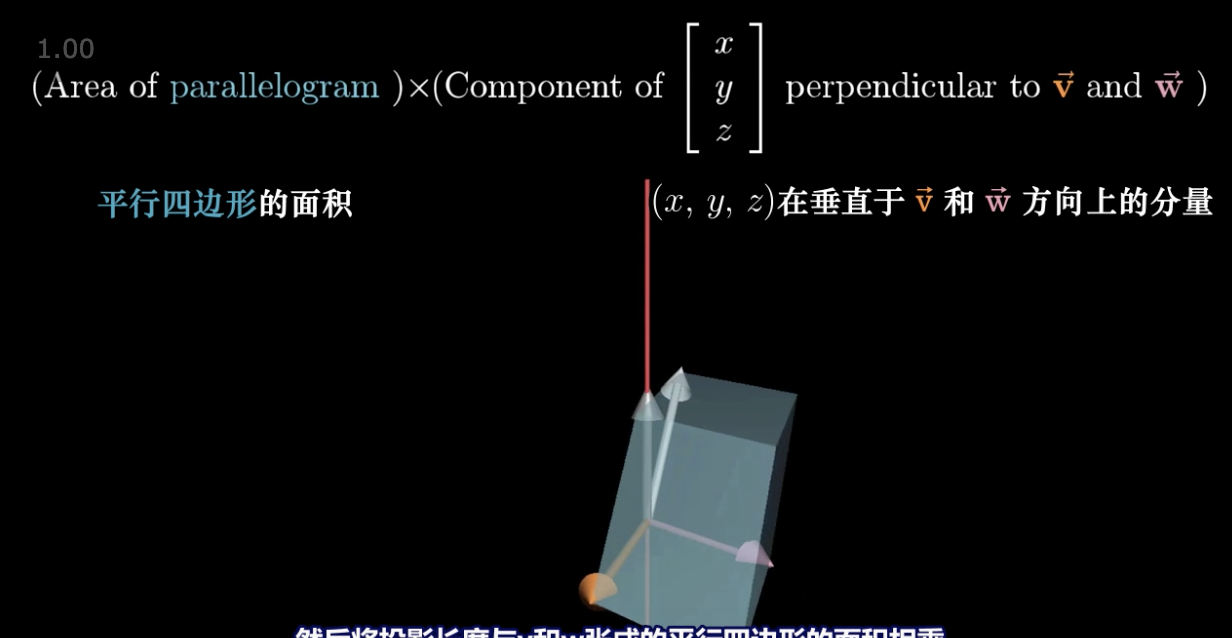
我们以 v，w为底的平行四边形乘以向量 p 在垂直于平面的投影得到的体积，必然等于垂直于 v 和 w 且长度为平行四边形面积的向量与（x，y，z）点乘是同一回事。
