【线性代数的本质】点积与对偶性

线性代数的本质，源视频 https://www.bilibili.com/video/BV1ys411472E

点积与对偶性

什么是点积？

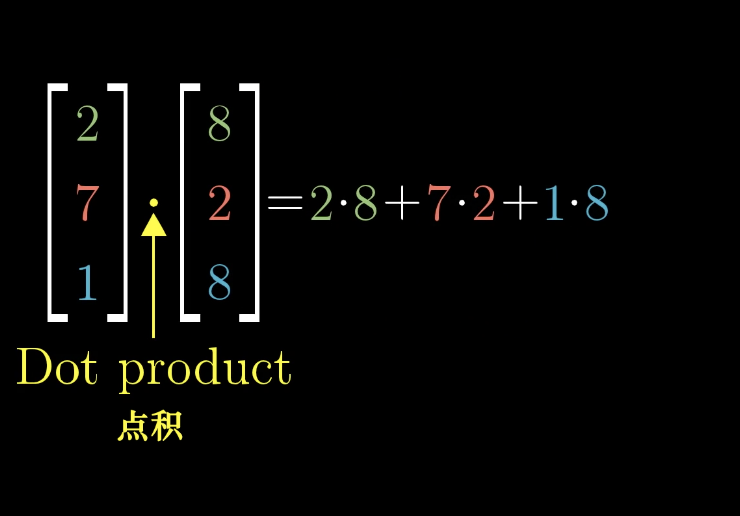
• 计算层面
  对于两个维数相同的向量，求它们的点积，就是将相应坐标配对，求出每一对坐标的乘积然后相加。
  
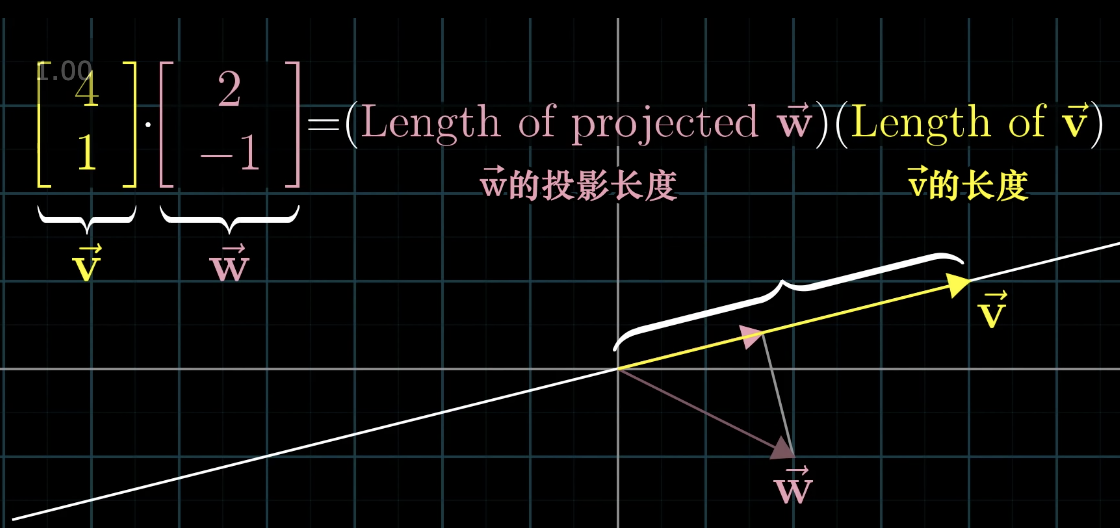
• 几何角度
  这是通常意义上的点积，下面我们将来理解集合上的意义，就是将一个向量投影到另外一个向量的方向上，然后乘以另外一个向量的长度，就得到了点积。
  

为什么两个点积投影的方向可以不一样呢？
我们可以用对称性来说明。

为什么这两种方式有联系？他们的联系又在哪里呢？

对于一个 1x2 的向量，我们可以将它转换到一维数轴上去理解.
向量的第一个相当于是转换过的 i，第二个相当于是转换过的 j，把它当成一种特殊的线性变换。

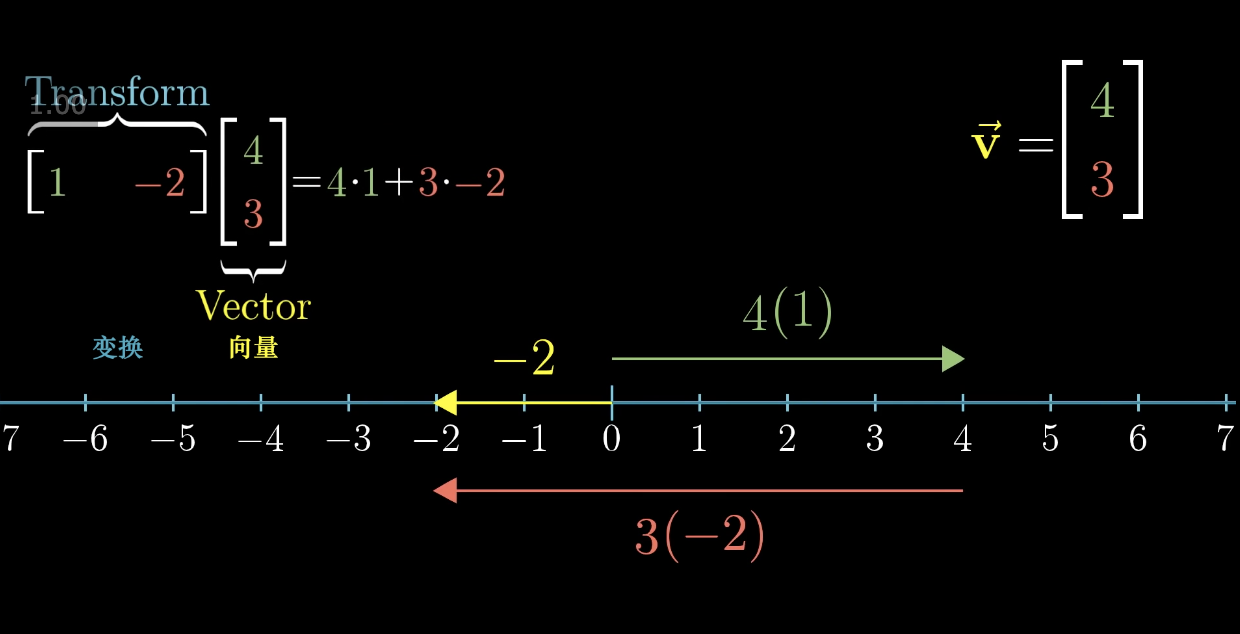
我们任何时候看到一个线性变换，它的输出空间是一维数轴，无论它是什么形式，空间中会存在唯一的向量 v 与之对应，在这个意义上，应用线性变换与向量 v 做点积是一样的。

对偶性 = 自然而又出乎意料的对应关系。