【线性代数的本质】矩阵、线性变换、矩阵乘法与线性变换复合
线性代数的本质，源视频 https://www.bilibili.com/video/BV1ys411472E
@
Unfortunately, no one can be told what the Matrix is. You have to see it for your self.
------ Morpheus
矩阵是什么？
矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。
在线性代数中，最容易被忽略但是非常重要的一点就是线性变换的概念以及它和矩阵的关系。
矩阵和线性变换
对于变换，变换其实就是函数的另外一种说法，它接受一个输入，然后输出对应的结果。
特别的，在线性代数下，我们考虑的是接受一个向量并且输出一个向量的变换。
为什么要用变换呢？
因为变换是在暗示以特定的方式来可视化这 输入-输出 关系，一种理解向量的函数的方式是使用运动。
例如在二维空间中，我们将一个输入向量移动到输出向量的位置，要理解整个变换，我们可以想象每一个输入向量输出到对应输出向量的位置。
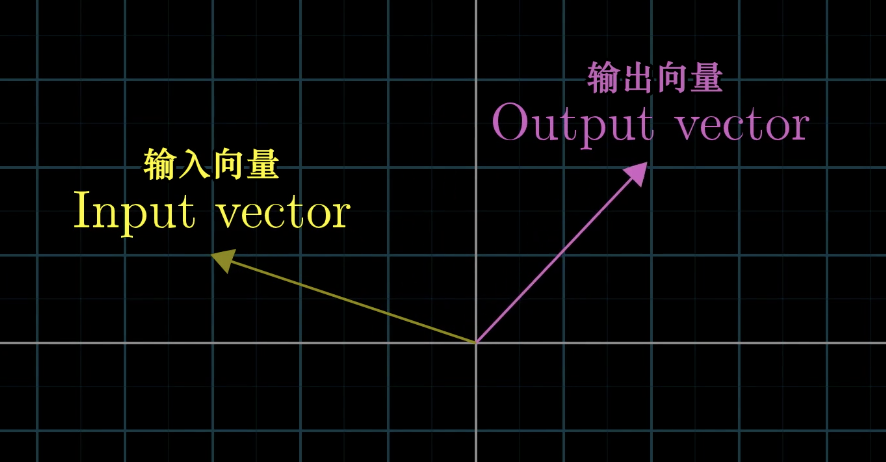
二维空间在这种变化时候，我们可以对无限网格上的所有点同时做变换，还可以保留原来坐标的网格，以便追踪起点和终点的位置。
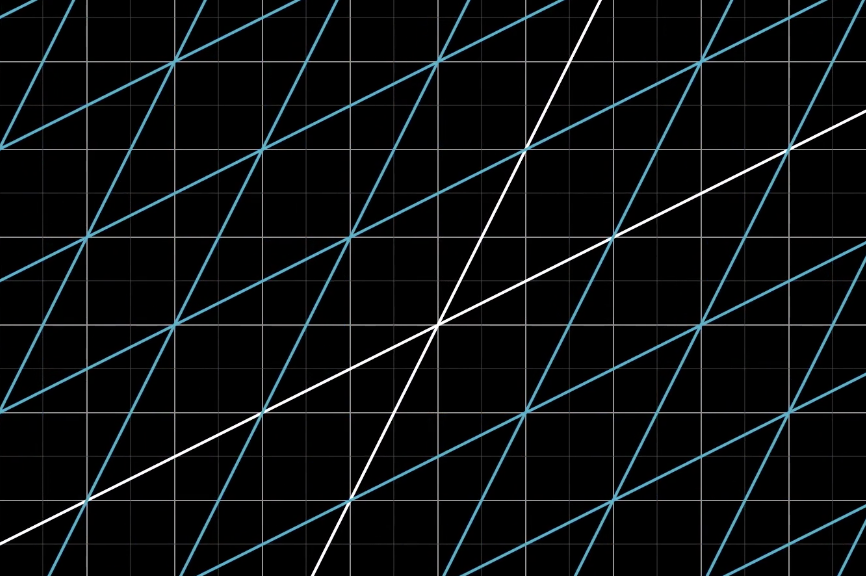
那么什么是线性变换呢？变换需要满足下面两个条件：
- 直线在变换之后仍然是直线，不能弯曲
- 原点必须固定
满足以上两个条件的变换就是线性变换。
例如，当我们把一个向量进行如下的线性变换时候，其实我们只需要记录原来的两个基向量进行变换之后的位置，即 i 和 j 向量进行变换之后的位置，其他所有的向量都会变化。
例如我们考虑（-1，2）这样一个向量，变换后的向量 v 的位置，是 -1 和变换后的 i 之积，加上 2 与变换之后的 j 之积，换句话说，v 向量是 i 与 j 向量的线性组合，而变换之后的向量，也是变换之后 i 和 j 的线性组合。
所以我们只要需要直到变换后的 i 和 j 向量的位置即可。
例如对于一个如下的变换，就可以这样计算：
我们只需要四个数字就可以确定一个线性变换即可！
在这里矩阵只是一个包含线性变换信息的组合。对于更普遍的情况，我们可以得到如下变换：
有了以上基础，我们可以进行一下总结：
严格意义上说，线性变换是将向量作为输入和输出的一类函数。
可以将线性变换看作对空间的挤压伸展，它保持网格线平行且等距分布，并且保持原点不变
关键在于，线性变换由它对空间的基向量的作用完全决定。
在二位空间中就是单位正交的基向量，因为任意其他向量都能表示为基向量的线性组合
这意味着只要记录下 i-hat 和 j-hat 变换后的位置，就能计算出一个坐标为（x， y）变换后的坐标。
习惯上，将变换后的 i-hat 和 j-hat 的坐标为做一个矩阵的列，并且将两列分别与x和y相乘后加和的结果定义为矩阵向量乘积。
这样，矩阵代表一个特定的线性变换，而矩阵与向量相乘，就是将线性变换作用于那个向量
矩阵乘法与复合变换
在很多情况下，我们可能会有多个变换的组合，例如先把一个向量顺时针旋转90度，再进行 shear，这样就会得到两个变换。
我们如果把两个变换分别进行，与记录下“旋转与剪切”的总变换得到的结果是一样的。
此时我们就把这种捕捉到两个变换的矩阵称为复合变换。
但是这个过程需要从右往左读，这是因为复合函数的定义就是如此，f ( g ( x ) ) 。
所以我们需要计算出最终的 i 和 j 向量去哪里了，所以我们需要进行计算，我们先把 M1 的第一列可以看作经过变换后的 i 向量， 第二列可以看作变换后的 j 向量。
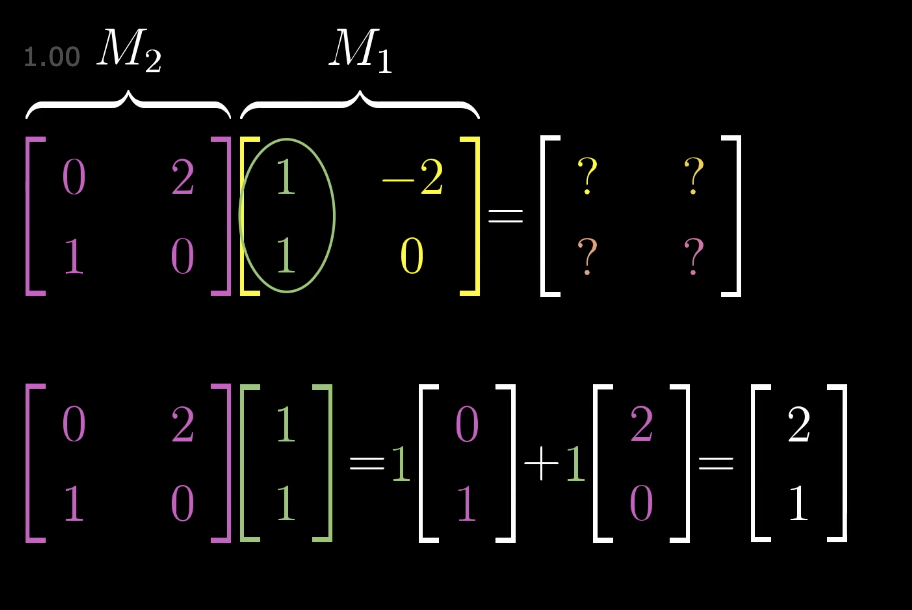
我们此时就得到了 i 向量，然后同样的方式可以得到 j 向量，此时我们就得到了矩阵乘法的意义以及复合变换的想法。
在记忆矩阵乘法的计算公式之前，更重要的是理解矩阵乘法的意义所在，然后再进行计算。
下面将进行行列式的学习。
