PTA-7-7 六度空间
本题考查点:
- 图的遍历方式
题目描述
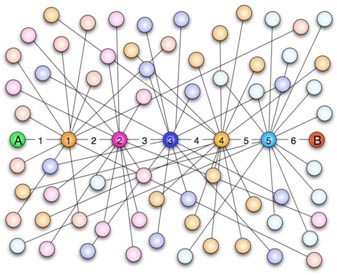
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”如图1所示。
图1 六度空间示意图“六度空间”理论虽然得到广泛的认同,并且正在得到越来越多的应用。但是数十年来,试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因,这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具,能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式:
输入第1行给出两个正整数,分别表示社交网络图的结点数N(1<N≤103,表示人数)、边数M(≤33×N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10输出样例:
1: 70.00% 2: 80.00% 3: 90.00% 4: 100.00% 5: 100.00% 6: 100.00% 7: 100.00% 8: 90.00% 9: 80.00% 10: 70.00%
这个题其实就是考察图的遍历方式,需要在 DFS 和 BFS 中做出抉择,哪一个更好。
我一开始选择的是图的DFS,后来发现在某情况下会有问题,也就是当 如果说我们采用 DFS 的话,会有这个问题,这也是我遇到的:
DFS不对是因为没有考虑到所有长度为6的路径
比如DFS先走了一条路走到第六步到了节点B
此时你标记了B之后不再走它(这是错误的
但是B如果和起始点相连,那么它也可以走一步就到B
这就是我在一开始用 DFS 的时候最后一个测试点总是通不过的原因。
所以我们采用 BFS,而且此时我们由于需要保存层数,我们新建一个结构体,用来在 BFS 的时候保存层数即可。
struct Node
{
int data, layer;
Node(int _data, int _layer) : data(_data), layer(_layer) {}
};
然后我们在进行 BFS 的时候进行构造即可,而且我们很早的就进行 BFS 的停止,也就是当第一个距离为 7 的结点出现的时候,我们就可以停止了,这个时候不仅仅能够提前结束遍历而且效率更高。
完整的的代码如下:
/*
Author: Veeupup
*/
#include <iostream>
#include <cstdio>
#include <cstdint>
#include <vector>
#include <queue>
using namespace std;
const int maxn = 1010;
int n, m; // 结点数(从 1~N 编号),边数
vector<int> Adj[maxn]; // 记录图
bool vis[maxn] = {false}; // 默认设置为未访问
struct Node
{
int data, layer;
Node(int _data, int _layer) : data(_data), layer(_layer) {}
};
int BFS(int nowVisit)
{
int ans = 0; // 不超过 6 的结点的个数
queue<Node> myQ;
myQ.push(Node(nowVisit, 0));
vis[nowVisit] = true;
while (!myQ.empty())
{
Node topNode = myQ.front();
myQ.pop();
int nowLayer = topNode.layer;
int nowId = topNode.data;
if(nowLayer == 7)
break;
ans++;
for (int i = 0; i < Adj[nowId].size(); i++)
{
int nextId = Adj[nowId][i];
if(vis[nextId] == false) {
vis[nextId] = true;
myQ.push(Node(nextId, nowLayer + 1));
}
}
}
return ans;
}
void BFSTravel()
{
for (int i = 1; i <= n; i++)
{
fill(vis, vis + maxn, false); // 设定为未访问过
int ans = BFS(i);
printf("%d: %.2f%%\n", i, (ans * 1.0) / n * 100);
}
}
void DFS(int nowVisit, int depth, int &allNodes, int &sixNodes)
{
for (int i = 0; i < Adj[nowVisit].size(); i++)
{ // 遍历所有能够到达的边
int nextId = Adj[nowVisit][i];
if (vis[nextId] == false)
{
vis[nextId] = true;
allNodes++;
if (depth <= 6)
{
sixNodes++;
}
DFS(nextId, depth + 1, allNodes, sixNodes);
}
}
}
void DFSTravel()
{
for (int i = 1; i <= n; i++)
{
fill(vis, vis + maxn, false);
int allNodes = 0, sixNodes = 1; // 记录所有能到达的点,在6点之内能到达的点
vis[i] = true;
DFS(i, 1, allNodes, sixNodes);
printf("%d: %.2f%%\n", i, (sixNodes * 1.0) / n * 100);
}
}
int main()
{
freopen("data.txt", "r", stdin);
scanf("%d%d", &n, &m);
int v1, v2;
for (int i = 0; i < m; i++)
{ // 读入图
scanf("%d%d", &v1, &v2);
Adj[v1].push_back(v2);
Adj[v2].push_back(v1);
}
BFSTravel();
return 0;
}
希望对大家有帮助。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号