[What-Why-How] 线性回归预测
What
现有多个变量X1, X2, X3, ....会对结果数据Y产生影响,现在要求出这些变量Xn对于最终结果的影响权重。找到一个线(两个变量),面(三个变量)来拟合这些权重的数值。通过训练数据得到这些参数,然后使用这些参数(模型)对新数据进行预测
例如,拟合一个平面:
![]()
其中 θ0表示预置的权重参数。
-
误差
真实值和预测值之间肯定是要存在差异的
误差是独立并且具有相同分布,并且服从均值为0方差为θ2的高斯分布(正态分布)
似然函数:![]() ,什么样的参数跟我们的数据组合后恰好时真实值。 样本数据 -> 参数,参数估计。最大似然函数,极大似然估计,让结果符合真实值的概率最大。
,什么样的参数跟我们的数据组合后恰好时真实值。 样本数据 -> 参数,参数估计。最大似然函数,极大似然估计,让结果符合真实值的概率最大。
对数似然:![]() ,似然函数的对数形式,便于计算。
,似然函数的对数形式,便于计算。
目标函数:![]() ,从对数似然化简得出,目标函数值越小似然函数值越大。对目标函数求偏导,在其偏导数为0点的,为极小值点:
,从对数似然化简得出,目标函数值越小似然函数值越大。对目标函数求偏导,在其偏导数为0点的,为极小值点:![]()
-
评估方法
最常用的评估项:R2,其值越接近1认为结果约好。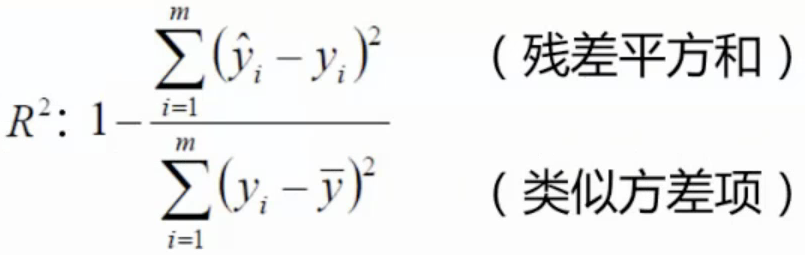
-
梯度下降
得到一个目标函数后,如何进行求解。
目标函数:![]() ,寻找山谷最低点,即函数终点
,寻找山谷最低点,即函数终点
如果有多个参数,是每个参数分布求极值,每次一小点,不断的更新参数
梯度下降的方法:
-
-
批量梯度下降
![]()
-
容易得到最优解,但每次要考虑所有样本,速度很慢
-
-
随机梯度下降
![]()
-
每次找一个样本,迭代速度快,但不一定每次朝着收敛的方向
-
-
小批量梯度下降 batch
![]()
-
每次更新选择一小部分数据来计算,较实用
不同步长(学习率)对结果会有大影响。一般要小一些,从小值开始,不行再小。批量的大小,在机器资源允许的情况下尽量大些。
Why
How



 浙公网安备 33010602011771号
浙公网安备 33010602011771号