牛顿迭代法求平方根。

参考链接：http://www.matrix67.com/blog/archives/361

https://www.zhihu.com/question/20690553

https://www.jianshu.com/p/dcd73888ac3a

核心思想：以直代曲。切线是曲线的线形逼近。

x^2 = a ---- 》 f(x) = x^2-a, 该函数导数f'(x)=2x.

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数 f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。首先我们先来看函数图像。

 

 

 

 

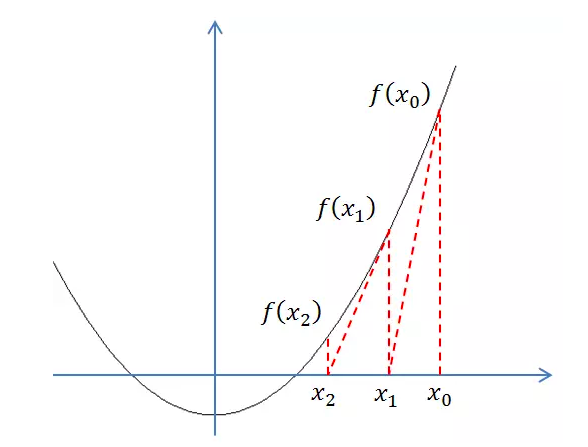
首先，选择一个接近函数f(x)零点的x0,计算相应的f(x0)和切线斜率f'(x0)（这里f'表示函数f的导数)。
也就是求如下方程的解：

 

我们将新求得的点 x坐标命名为x1，通常x1会比x0更接近方程f(x)=0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示：

 

----------------------------

 

代码：

 public static double sqrt_newton(double c){
        if (c < 0 ) return Double.NaN;
        double err = 1e-15;
        double t = c;
        while (Math.abs(t-c/t) > err*t){
            t=(c/t + t)/2.0;
        }
        return t;
    }