线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

（1）本节课的内容思维导图

 

监督学习：可以用于映射出该实例的类别。

无监督学习：我们只知道特征，并不知道答案，不同的实例具有一定的相似性，把那些相似的聚集在一起。

 

（2）回归与分类的区别

回归与分类的区别最主要是要看预测的目标函数是否连续，连续变量预测的为回归，例如：预测明天的气温是多少度，这是回归任务，而对离散变量的预测称为分类，例如：预测明天天气是晴还是阴，这是一个分类任务，做预测前首先要分清他是回归任务还是分类任务，这样才能选择合适的算法预测。

（3）回归算法可以运用的领域

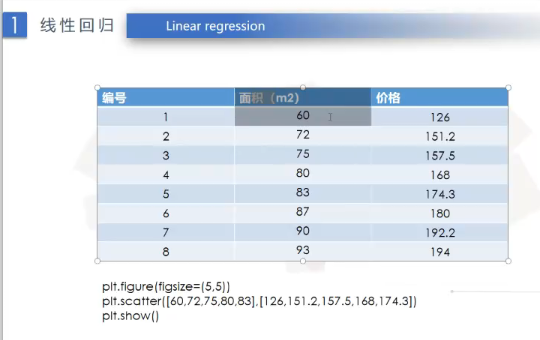
1)房价预测

 

 

 

面积对价格的影响

 

 

 

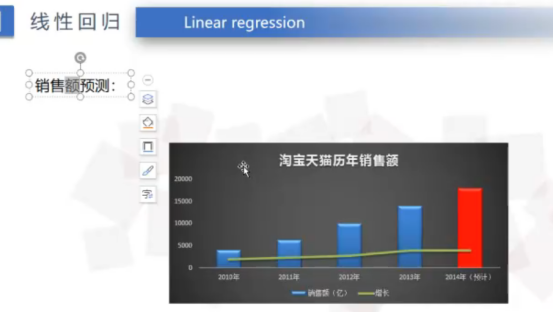
2）销售额的预测

 

 

 

3）贷款额度的预测

 

（4）线性关系模型

 

（5）数组与矩阵的运算

数组：

0维：1,2,3

1维：[1,2,3]

2维：[[1,2,3],[4,5,6]]两行三列2*3

3维：[[[1,2,3],[4,5,6],[4,5,6],[4,5,6]]]

矩阵:

1.矩阵必须是二维的

2.矩阵满足了特殊的运算要求

相同的内容，执行数组与矩阵的乘法运算

 

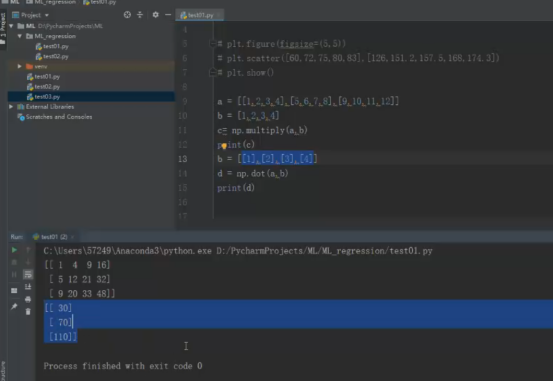
数组的乘法运算：

[[1,2,3,4],                        [[1*1,2*2,3*3,4*4],          [[1,4,9,16],

[5,6,7,8],    *  [1,2,3,4]=   [5*1,6*2,7*3,8*4],    =      [5,12,21,32],

[9,10,11,12]]                   [9*1,10*2,11*3,12*4]]      [9,20,33,48]]

矩阵的乘法运算：（两个矩阵相乘，前者的列数一定与后者的行数相等(m行*n列) *（h行*k列）=(m行,k列）

主要方法：用左边矩阵的第一行，逐个乘以右边矩阵的列，第一行与第一列各个元素的乘积相加，第一行与第二列的各个元素的乘积相加...

[[1,2,3,4],         [ [1],               [[1*1+2*2+3*3+4*4],      

[5,6,7,8],    *     [2],       =       [5*1+6*2+7*3+8*4],       =     [[30],[70],[110]]

[9,10,11,12]]     [3],               [9*1+10*2+11*3+12*4]]

                         [4] ]   

矩阵的这种运算正好可以满足了线性回归的计算基础，所以我们首先要学会矩阵的运算

（6）损失函数

 

 

 

（7）两种减少误差的方式

1)最小二乘法之正规方程

 

 

 

T：将矩阵转置（行变列，列变行）

X^-1 :求逆矩阵（X*？=单位矩阵 ，？就是x的逆矩阵）

2）最小二乘法之梯度下降法

 

 

 

 

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率。

在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向。

代码

import random
import time
import matplotlib.pyplot as plt

# 创建数据
_xs = [0.1 * x for x in range(0, 10)]
_ys = [12 * i + 4 for i in _xs]
print(_xs)
print(_ys)

w = random.random()   #权重
print(w)
b = random.random()   #偏置
print(b)
# y=wx+b
a1 = []
b1 = []
for i in range(1):
    for x, y in zip(_xs, _ys):  #遍历_xs和_ys
        print("x=",x,"y=",y)
        o = w * x + b           #预测值
        print("o=")
        e = (o - y)             #误差
        print("e=",e)
        loss = e ** 2           #平方损失函数
        dw = 2 * e * x          #对(w*x+b)^2求w的偏导数，梯度
        db = 2 * e * 1          #对(w*x+b)^2求b的偏导数，梯度
        w = w - 0.1 * dw        #梯度下降w
        b = b - 0.1 * db        #梯度下降b
        print('loss={0},w={1},b={2}'.format(loss, w, b))
    a1.append(i)
    b1.append(loss)
    plt.plot(a1, b1)
    plt.pause(0.1)
plt.show()

循环10次,损失loss还比较大，w和b里实际值12,4还相差较大

 

 

 

随着训练次数的变化Loss值的变化：

 

 

 

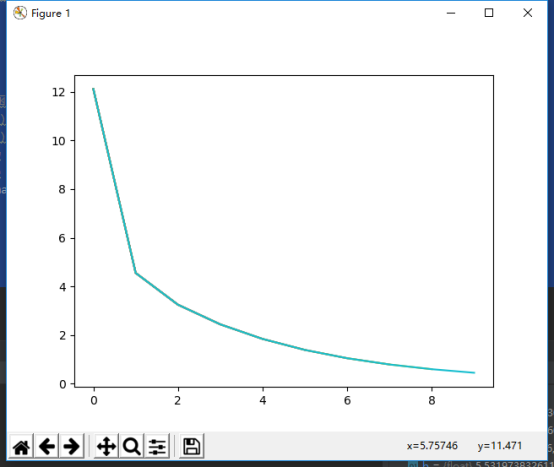
循环100次，损失变小，w和b更加接近实际值

 

随着训练次数的变化Loss值的变化：

 

 

 

 

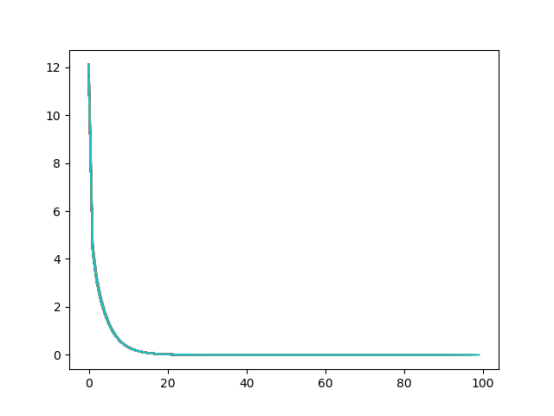
2.思考线性回归算法可以用来做什么？

线性回归算法除了上课时提到的预测房价，预测销售额，预测贷款额度之外，它也可以用来预测一个人的信用、预测山体滑坡的概率，预测是否交通堵塞等等。

2.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

通过网上获取：

实现：通过房屋的朝向，建造时间，有无电梯 ，楼层高低，面积㎡，装修程度以及室厅房情况运用线性回归算法预测房屋价格

 数据来源：

文件为从https://guangzhou.leyoujia.com/esf/乐有家官网爬取的数据
房屋朝向特征化：
南：0
东：1
北：2
西：3
房屋有无电梯特征化：
暂无：0
有电梯：1
房屋楼层特征化：
高楼层：0
中楼层：1
低楼层：2
装修程度特征化：
普装：0
精装：1
毛呸：2
豪装：3

import pandas
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# 文件为从https://guangzhou.leyoujia.com/esf/乐有家官网爬取的数据
# 201706120019hdfend.csv文件为处理有导出的数据文件
# 房屋朝向特征化：
# 南：0
# 东：1
# 北：2
# 西：3
# 房屋有无电梯特征化：
# 暂无：0
# 有电梯：1
# 房屋楼层特征化：
# 高楼层：0
# 中楼层：1
# 低楼层：2
# 装修程度特征化：
# 普装：0
# 精装：1
# 毛呸：2
# 豪装：3
data =pandas.read_csv('./venv/data/房产信息.csv')
x=data.loc[:, ['朝向', '时间', '电梯','楼层','面积㎡', '室', '厅', '房', '装修程度']]
print(x)
y=data.iloc[:,9]
print(y)
# 划分训练集与测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.1,random_state=5)#划分训练集与测试集
print("x的训练集为：",x_train)
print("y的训练集为：",y_train)
# 构建线性LinearRegression回归模型
LR_model=LinearRegression()
LR_model.fit(x_train,y_train)   # 训练模型
print("线性回归模型构建完成：\n",LR_model)
# 用模型调用预测数据，预测结果
LR_pre=LR_model.predict(x_test)
print('回归模型的权值：',LR_model.coef_)
print('回归模型的截距项：',LR_model.intercept_)
#绘制线性回归模型折线图
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置字体为SimHei显示中文
plt.rcParams['axes.unicode_minus'] = False # 设置正常显示字符
p=plt.figure(figsize=(12,30))  # 确定画布大小
plt.subplot(3,1,1)  # 分为三行一列，放在位置1
plt.title("预测结果折线图")
p1=plt.plot(range(y_test.size),y_test,color="#2FBE95")  # 绘制真实值折线图
# bbox_to_anchor(num1,num2)表示legend的位置和图像的位置关系，num1表示水平位置，num2表示垂直位置。
plt.legend(["预测值"],bbox_to_anchor=(1.01, 0.8), loc=3, borderaxespad=0) # 图例
plt.subplot(3,1,2)  # 分为三行一列，放在位置1
plt.title("真实结果折线图")
plt.plot(range(y_test.size),LR_pre,color="#2A4C68")  # 绘制预测值折线图
plt.legend(["真实值"],bbox_to_anchor=(1.01, 0.8), loc=3, borderaxespad=0) # 图例
plt.subplot(3,1,3)  # 分为三行一列，放在位置1
plt.title("预测与真实值对照折线图")
plt.plot(range(y_test.size),y_test,color="#2FBE95")  # 绘制真实值折线图
plt.plot(range(y_test.size),LR_pre,color="#2A4C68")  # 绘制预测值折线图
plt.legend(["真实值","预测值"],bbox_to_anchor=(1.01, 0.8), loc=3, borderaxespad=0) # 图例
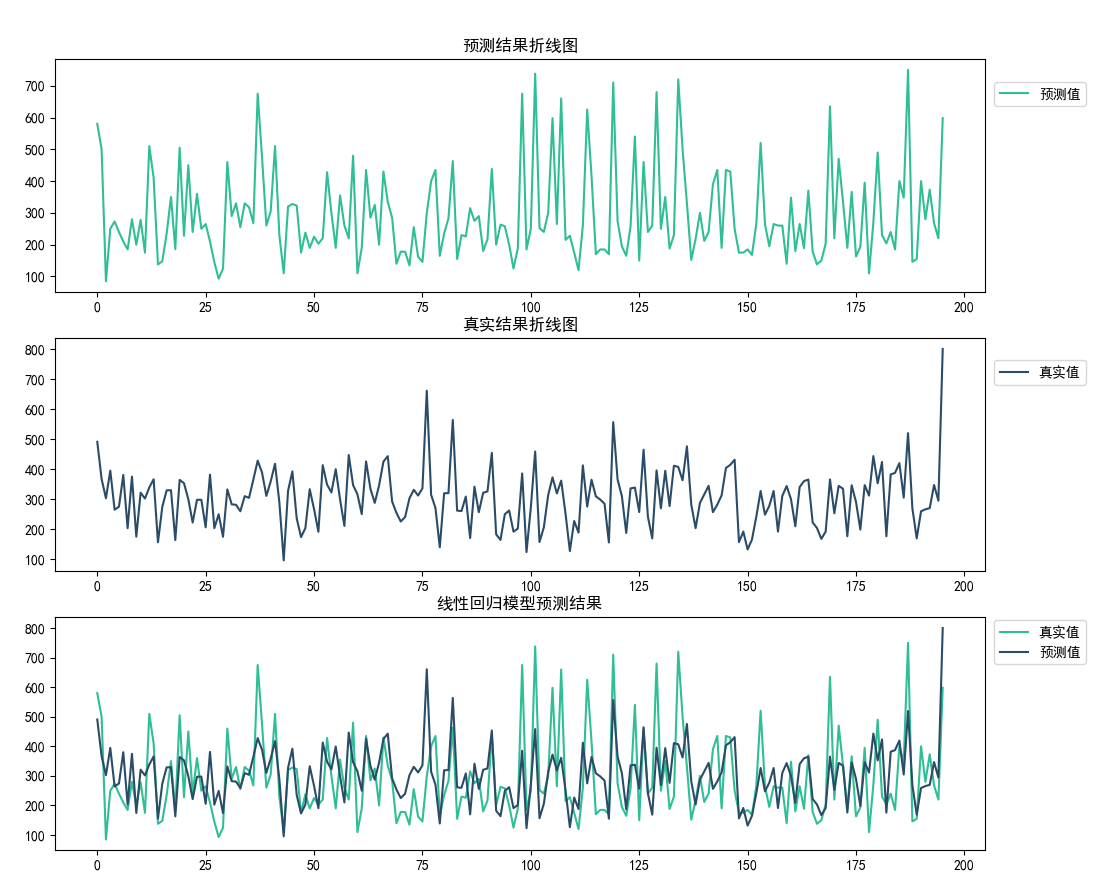
plt.title("线性回归模型预测结果")
plt.show()

数据详情

 

x

 

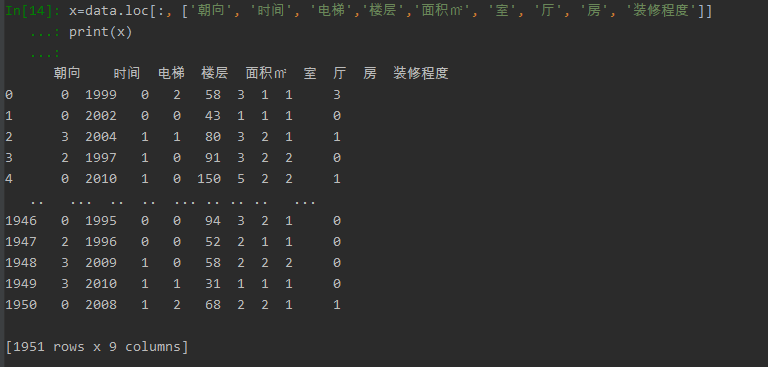
目标值y

 

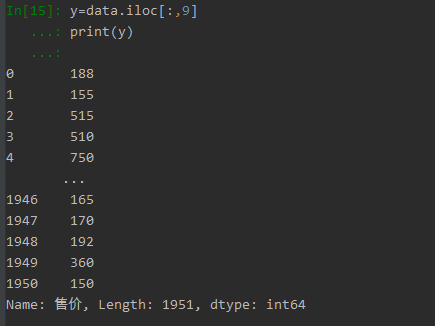
模型预测结果