机器学习相关数学基础

学习记录：

 

 

 

 

1.梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模)

在向量微积分中，标量场的梯度是一个向量场。标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。更严格的说，从欧几里得空间Rn到R的函数的梯度是在Rn某一点最佳的线性近似。在这个意义上，梯度是雅可比矩阵的特殊情况。

在单变量的实值函数的情况，梯度只是导数，或者，对于一个线性函数，也就是线的斜率。

梯度一词有时用于斜度，也就是一个曲面沿着给定方向的倾斜程度。可以通过取向量梯度和所研究的方向的点积来得到斜度。梯度的数值有时也被称为梯度。

 

2.梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：一个人被困在山上，需要从山上下来(i.e. 找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

 

J是关于Θ的一个函数，我们当前所处的位置为Θ0点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是α，走完这个段步长，就到达了Θ1这个点

 

 

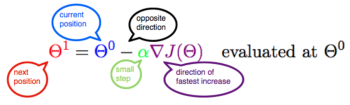
α是什么含义？
α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离。

 

 

 

为什么要梯度要乘以一个负号？
梯度前加一个负号，就意味着朝着梯度相反的方向前进！梯度的方向实际就是函数在此点上升最快的方向，而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号。

 

3.贝叶斯定理是关于随机事件A和B的条件概率（或边缘概率）的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性

贝叶斯公式（发表于1763年）为：

一些文献中把P(B)、P(B)称为基础概率，P(A│B)为击中率，P(A│B[2])为误报率。其实就是在运用概率对某一事件进行推断之前，我们往往已经事先掌握了关于这一事件的概率，这个概率可能是主观概率或者相对概率，这种初始的概率可以称为先验概率。如果在后续的研究中，通过抽样调查样本等消息源又获得了有关该事件的信息，我们就可以根据这些新信息对先验概率进行修正，使先验概率变为后验概率。这个修正概率的定理就称为贝叶斯定理。