【转载】四维空间中的超方形（HyperCube）研究

转自: https://home.gamer.com.tw/creationDetail.php?sn=2427438

二維空間（二次元）：正方形

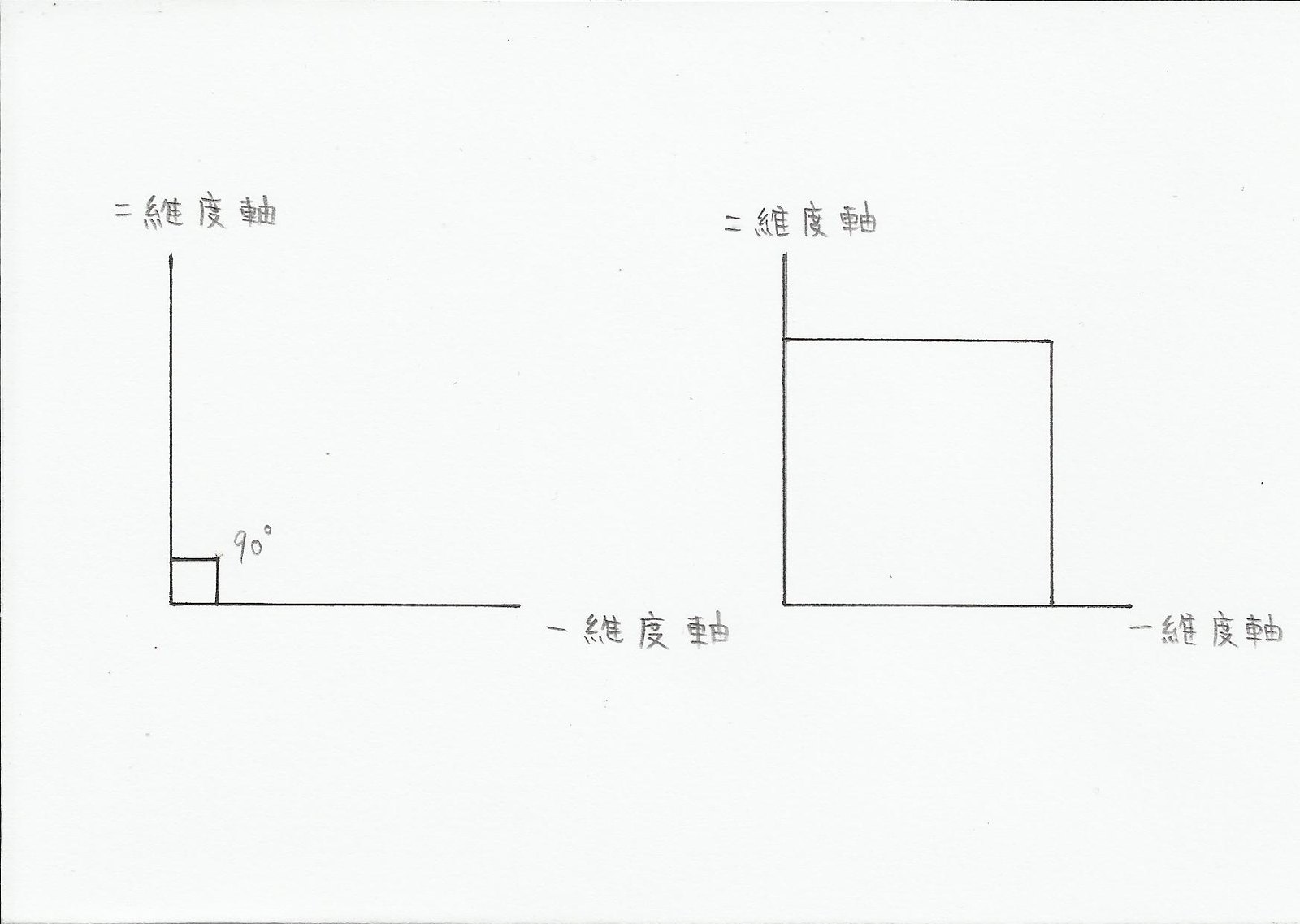
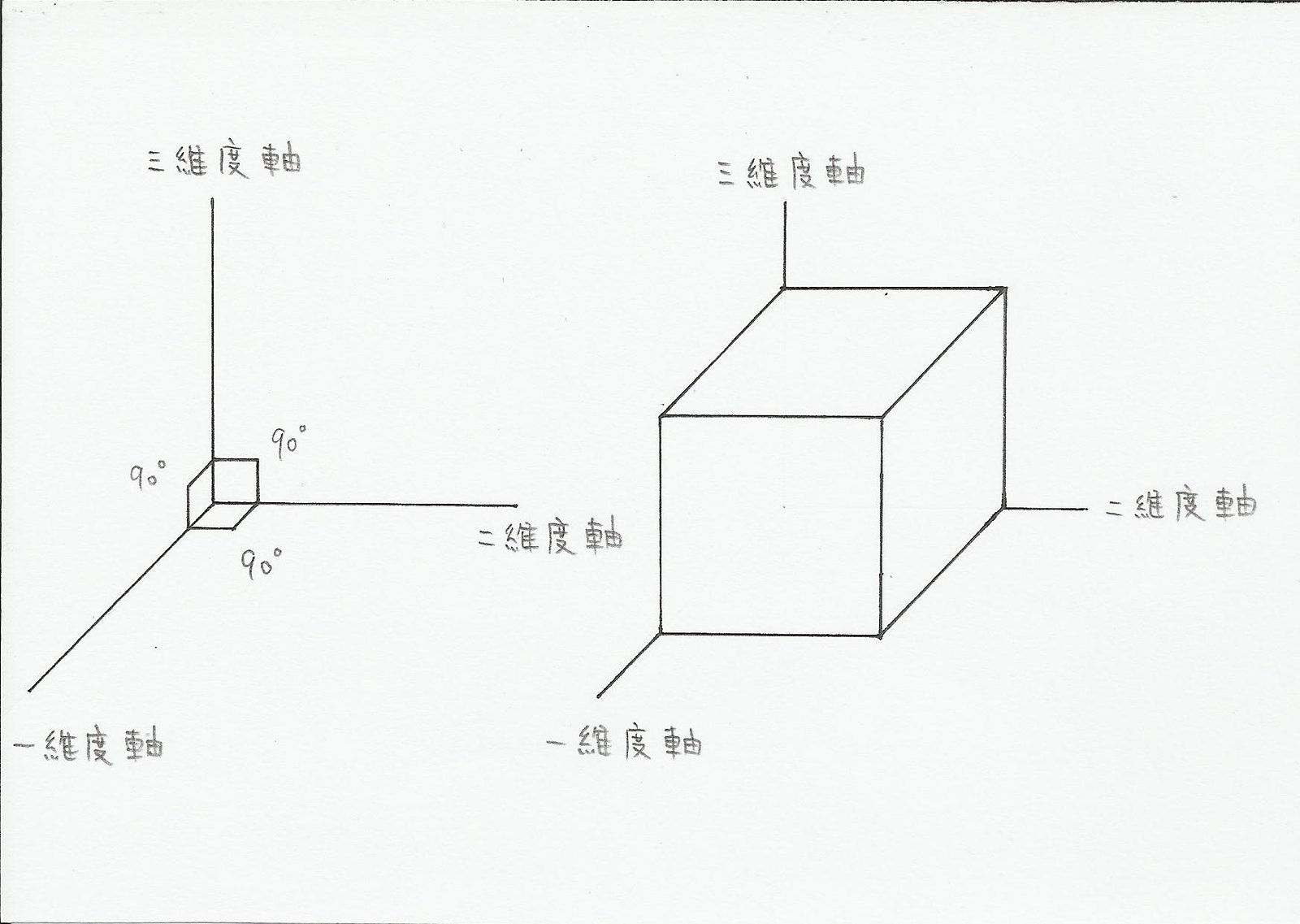
三維空間（三次元）：正方體

四維空間（四次元）：正方晶（超正方體）

※正方晶名稱由來是因為模型在三維空間看起來像一個結晶體，但在學界上是稱為超正方體、超方形。

正方晶推演過程

二維空間　＞＞　三維空間　＞＞　四維空間

正方形　　＞＞　正方體　　＞＞　正方晶

二維空間　＞＞　兩個維度所構成　＞＞　兩個維度軸夾角90度

正方形　　＞＞　四邊等長的邊所圍成且四個夾角都為90度

三維空間　＞＞　三個維度所構成　＞＞　三個維度軸，各軸彼此夾角90度

正方體　　＞＞　長寬高等長所構成的立方結構，長寬高彼此夾角都為90度

正方形和正方體都是在現實生活中會出現，是可以理解的概念

接下來就開始解釋正方晶是如何推演出來的

假設每個邊長長度為1

二維空間－正方形　座標表示（二維，一維）

（0，0）（0，1）（1，0）（1，1）

共4點，2^2個點

正方形是正方體的基本結構，可以用來推演出正方體

三維空間－正方體　座標表示（三維，二維，一維）

（0，0，0）（0，0，1）（0，1，0）（0，1，1）

（1，0，0）（1，0，1）（1，1，0）（1，1，1）

共8點，2^3個點

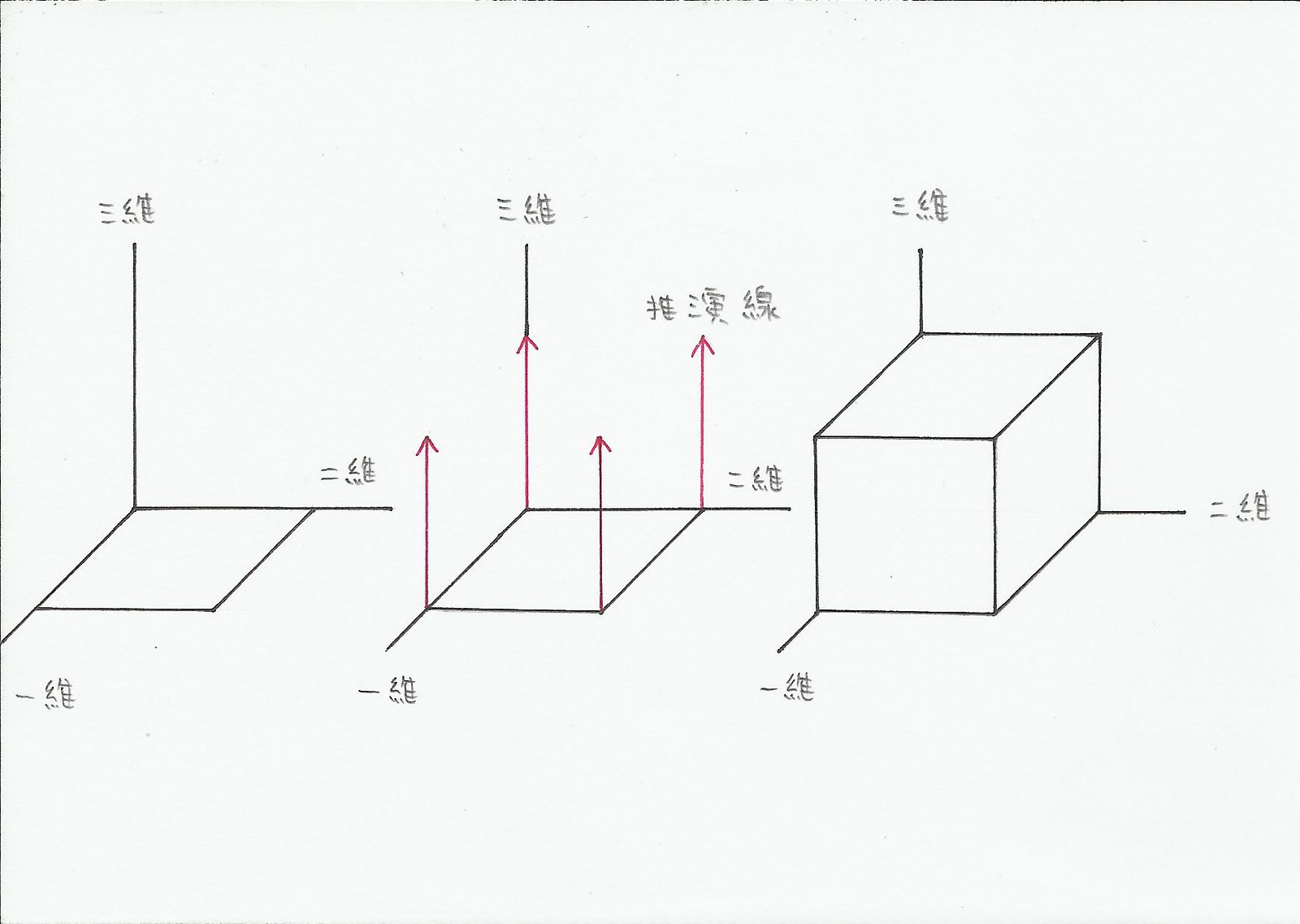
以圖推演

正方體是正方晶的基本結構，可以用來推演出正方晶

四維空間－正方晶　座標表示（四維，三維，二維，一維）

（0，0，0，0）（0，0，0，1）（0，0，1，0）（0，0，1，1）

（0，1，0，0）（0，1，0，1）（0，1，1，0）（0，1，1，1）

（1，0，0，0）（1，0，0，1）（1，0，1，0）（1，0，1，1）

（1，1，0，0）（1，1，0，1）（1，1，1，0）（1，1，1，1）

共16點，2^4個點

四維空間　＞＞　四個維度所構成　＞＞　四個維度軸，各軸彼此夾角90度

以圖推演

由於二維空間來表示正方晶會不容易看得懂，所以用三維空間模型來表示正方晶會較容易理解，為了能在三維空間更容易推演，需把三維度軸和四維度軸交換

圖中塗上紅色部分為推演線

正方晶邊數：正方體邊數＊2＋推演線＝12＊2＋8＝32個邊

正方晶面數：正方體面數＊2＋兩個推演線和兩個邊所構成的面＝6＊2＋12＝24面

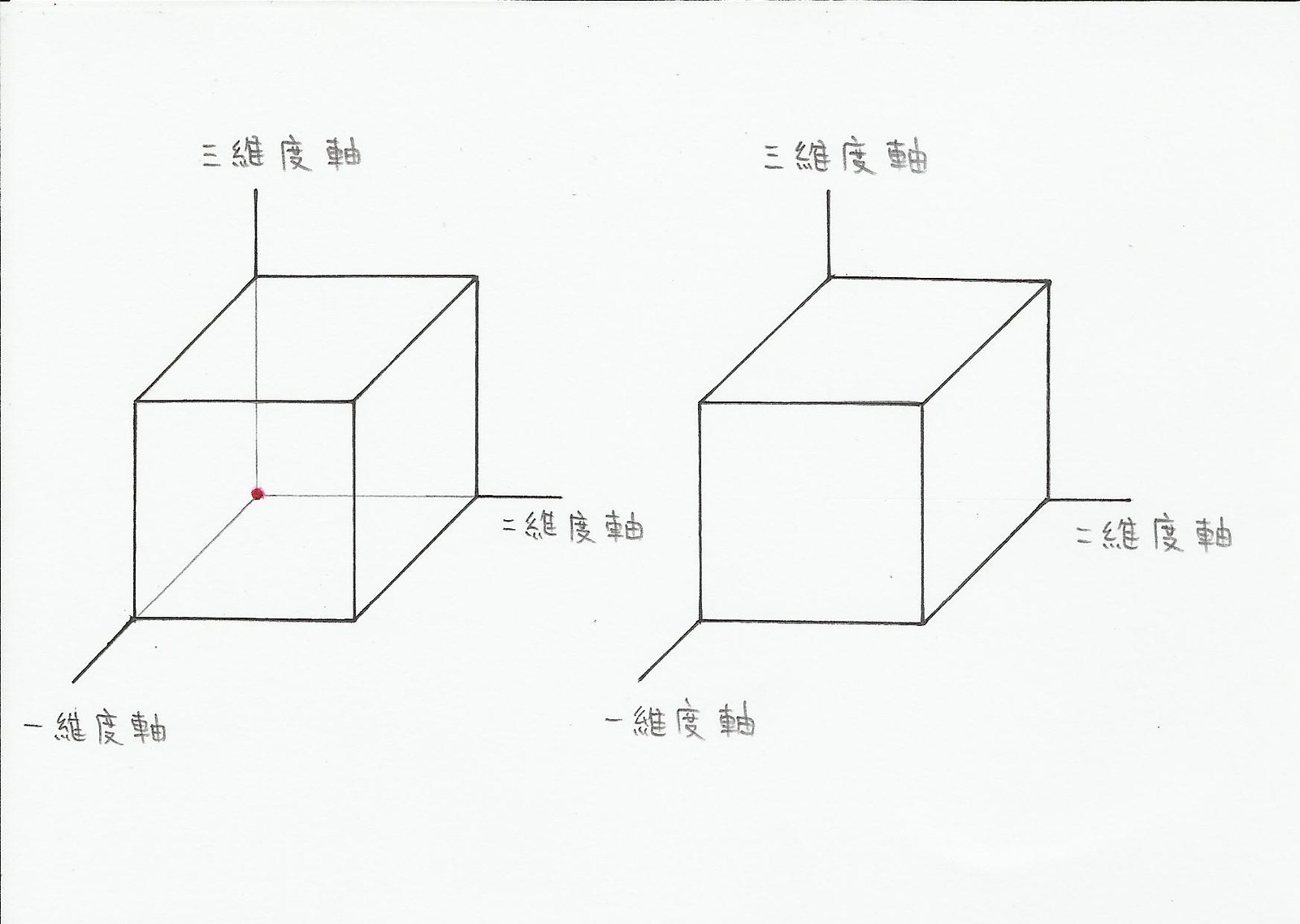
正方晶點數：14＋2＝16個點（2點是隱藏點）

二維空間表示正方體時也會有隱藏點

7＋1＝8個點（1點是隱藏點）

以圖說明，如果有二維空間的人類在觀察這個模型時，他不管怎麼旋轉模型就是看不到一個點，而這一點就被稱為隱藏點，但對三維空間的人類來看，隱藏點只是被遮住看不到而已

同樣的道理也適用於三維空間的正方晶模型，三維空間的人類不管怎麼翻轉模型就是看不到兩個點，對四維空間的人類來看也只是被遮住看不到而已

圖中紅點為隱藏點

正方晶的隱藏點（紅色指標所指的兩點）

以下為正方晶模型