【转载】Fisher Vector 通俗理解
转自: https://blog.csdn.net/u012192662/article/details/41644197
核心:
Fisher vector本质上是用似然函数的梯度vector来表达一幅图像
基础知识的预备:
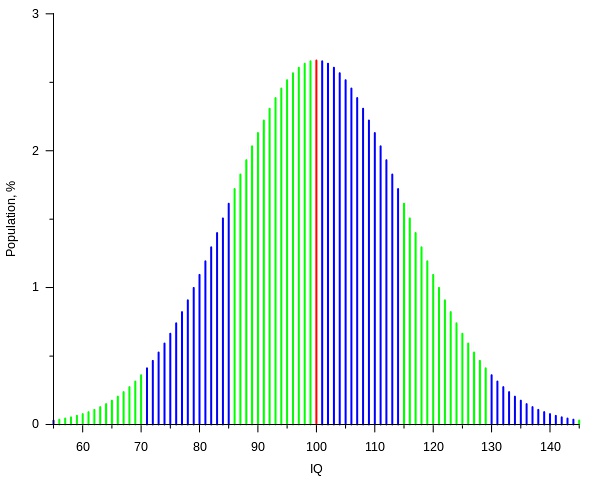
1. 高斯分布
生活和自然中,很多的事和物的分布都可以近似的看做是高斯分布。比如说:一个班的成绩的优良中差的分布。最优秀的和最差的往往都是少数,一般人是大多数。
高斯分布直观的感受是这样的:这是这种分布的概率情况的表示:
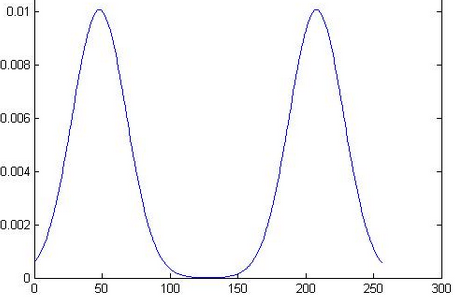
2. 混合高斯分布
问题是:一个班的成绩的分布他也可能是这样的:60分以下以及95分以上很少人,60-75很多人,突然75-85人又少了,但是85-90又多了。这个时候直观的感受是这样的:
这个时候很显然若使用两个高斯分布来拟合,加上二者的权重效果比单个的高斯分布要好得多!若是不止两个山峰那最好就是再多几个高斯的分布同时来拟合。所以我对GMM(Gaussian Mixture Model)理解。
3.高斯分布用于图像
相信大家对于独立同分布(i.i.d)还是知道的。对于图像也是,它表示为你用来表示这样图像的特征的哥哥维度之间是独立的。拿一个人来说,我们如果用它的身高、体重、三维来代替他。那这些就是他的特征了。对于他来说,这些特征就可以看做是独立同分布了。对于一个图像同样是这样。
而用到独立同分布最重要的原因是:你可以将一个样本(一张图片)的概率分布表示为各个特征维度上面的概率分布的乘积。即: 取对数以后则表示为各项的对数概率的和,这样就极大的降低了计算的难度。
4.流形学习(参考了:http://blog.pluskid.org/?p=533)
嵌入在高维空间中的低维流形:最直观的例子通常都会是嵌入在三维空间中的二维或者一维流行。比如说一块布,可以把它看成一个二维平面,这是一个二维的欧氏空间,现在我们(在三维)中把它扭一扭,它就变成了一个流形(当然,不扭的时候,它也是一个流形,欧氏空间是流形的一种特殊情况)。所以,直观上来讲,一个流形好比是一个
d 维的空间,在一个 m 维的空间中 (m > d) 被扭曲之后的结果。
5. Fisher Vector 的本质
Fisher
Vector的本质就是对于高斯分布-的变量求偏导!也就是对权重,均值,标准差求编导得到的结果。最后在需要一个归一化处理。具体的可以参照:
http://blog.csdn.net/carrierlxksuper/article/details/28151013
在此之前再定义一个变量:
,表征的是occupancyprobability,也就是特征xt是由第i个高斯分布生成的概率。
下面的公式给出了偏导计算公式:

值得注意的是上面求出来的都是没有归一化的vector,需要进行归一化操作,正如上一篇blog介绍的那样,由于是在概率空间中,与欧式空间中的归一化不同,引入Fisher matrix进行归一化。
公式4的三个变量分别引入三个对应的归一化需要的fisher matrix:
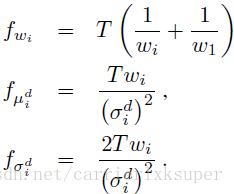
于是最终归一化之后的fisher vector就是:
由于每一个特征是d维的,需要K个高斯分布的线性组合,有公式5,一个Fisher vector的维数为(2*d+1)*K-1维。
这样得到的便是一张图片的特征了,便可以做视觉方面的操作勒。
6. 为什么Fisher Vector比高斯分布有效
我们将一张图近似为一个高斯分布,由这个高斯分布来表示这张图像。假设我们是做目标的检测,那么当你得到一个有相同的高斯分布的图的时候你就可以判断出这就是那个目标了。但实际的情况是却不一定是这样的,我们看一张图:
这两张图上特征点的分布在黑色的区域,二者的分布却可以一样(当然我画的不是很好)!
由此,我们知道,在高斯分布的基础上我们再找到变化的方向,我们便可以更加准确的表示这一张图!
我几乎是从道理上讲解的,细节还需要参考论文:Image Classification with the Fisher Vector: Theory and Practice. 等
好的,希望可以帮到你!
iker Cross
2014年12月2日


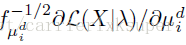
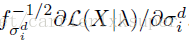


 浙公网安备 33010602011771号
浙公网安备 33010602011771号