【BZOJ 3270】博物馆
【原题题面】传送门
【题解大意】
设f[i][j]为a到i位置,b到j位置的概率。
转移方程很好搞,这里截个别人的图。
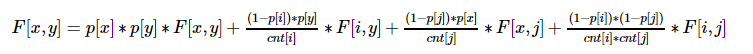
有个问题一直不明白,用来高斯消元的矩阵为什么要用边来消元。
下面是解释:
如果行列分别为1~n,那么a[i][j]这个系数在矩阵中只会出现一次,但是在本题中由指向该点的每一个点到点的概率所得到的概率值都是不相同的。
本题dp的阶段划分在于时间。
所以储存要矩阵需要储存相邻两个时刻a,b的位置,这样才能转移。
【code】

#include<bits/stdc++.h> #define rad 100000000 #define inf 1000000000 #define ll long long #define eps 1e-10 #define pa pair<ll,int> #define p(x,y) (x-1)*n+y using namespace std; int n,m,A,B,cnt,tot; int last[25],d[25]; double a[405][405],p[25]; vector<int> e[25]; void build(int x,int y) { a[p(x,y)][p(x,y)]--; for(unsigned int i=0;i<e[x].size();i++) for(unsigned int j=0;j<e[y].size();j++) { int tx=e[x][i],ty=e[y][j]; int t1=p(x,y),t2=p(tx,ty); if(tx!=ty) { if(tx==x&&ty==y) a[t1][t2]+=p[tx]*p[ty]; else if(tx==x) a[t1][t2]+=p[tx]*(1-p[ty])/d[ty]; else if(ty==y) a[t1][t2]+=p[ty]*(1-p[tx])/d[tx]; else a[t1][t2]+=(1-p[tx])*(1-p[ty])/d[tx]/d[ty]; } } } void gauss() { int now=1; for(int i=1;i<=tot;i++) { int j; for(j=now;!a[j][now]&&j<=tot;j++); for(int k=1;k<=tot+1;k++)swap(a[now][k],a[j][k]); for(int j=1;j<=tot;j++) if(j!=now) { double t=a[j][now]/a[now][now]; for(int k=1;k<=tot+1;k++) a[j][k]-=t*a[now][k]; } now++; } } int main() { scanf("%d%d%d%d",&n,&m,&A,&B); tot=n*n; a[p(A,B)][tot+1]=-1; for(int i=1;i<=n;i++)e[i].push_back(i); for(int i=1,u,v;i<=m;i++) { scanf("%d%d",&u,&v); d[u]++;d[v]++; e[u].push_back(v); e[v].push_back(u); } for(int i=1;i<=n;i++)scanf("%lf",&p[i]); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) build(i,j); gauss(); for(int i=1;i<=n;i++) { int t=p(i,i); printf("%.6lf",a[t][tot+1]/a[t][t]); if(i!=n)printf(" "); } return 0; }
G102的孤儿们都要好好的啊。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号