ACM 博弈(难)题练习 (第二弹)
第一弹:
Moscow Pre-Finals Workshop 2016 - Kent Nikaido Contest 1 Problem K. Pyramid Game
http://opentrains.snarknews.info/~ejudge/team.cgi?SID=afa73761fd0d61ae&action=2<=1
题意:
N堆石头,两个人轮流取。有2种操作:一是选择一堆石头拿走一个,二是从每堆石头拿走一个,但是只有当所有堆都非零的时候才能用第二种操作。 谁不能操作谁就输了。
题解:
1. 如果只有第一种操作,那么如果轮到某个人的时候剩下奇数个石头,他就可以赢。定义这样的局面是对他有利的。
2. 如果N为奇数,用第二种操作实际上不会改变局面对谁有利。 直接根据sum的奇偶判断。
3. 如果N为偶数,那么用一次第二种操作可以改变局面对谁有利。 考虑如果轮到某个人时,存在某一堆石头只有1个,那么如果当前局面对他有利,他直接用操作一拿走这个石头,如果对他不利,先手可以用一次操作二, 之后两个人都不能用操作二了。 所以不管怎样都是他赢。 换一个角度来看,如果某堆石头只有2个,那么显然不能去动它,否则就会把一个1留给对手。 因此问题转化为将每一堆石头都减去2个的子问题。 所以不断转化为子问题,只要考虑最少的那堆石头的奇偶性和sum的奇偶性就可以判断出答案了。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int main() 5 { 6 int n, a[100]; 7 cin >> n; 8 int s = 0, mi = 100; 9 for (int i = 1; i <= n; ++i) 10 { 11 cin >> a[i], s += a[i], mi = min(mi, a[i]); 12 } 13 14 if (n & 1) 15 { 16 if (s & 1) puts("Iori"); 17 else puts("Yayoi"); 18 } 19 else 20 { 21 if (mi & 1) puts("Iori"); 22 else 23 { 24 if (s & 1) puts("Iori"); 25 else puts("Yayoi"); 26 } 27 } 28 29 return 0; 30 }
XVIII Open Cup named after E.V. Pankratiev. Ukrainian Grand Prix Problem G Zenyk, Marichka and Interesting Game
http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=10396&locale_id=0
题意:
两个人玩取石子游戏,N堆石子,每次先手只能从某一堆石子里拿A个,后手只能从某一堆石子里拿B个,谁不能操作谁就输了。
题解:
1.如果A = B。显然对于一堆有$x$个石头的石子,只能操作$\lfloor \frac{x}{A} \rfloor $次,求和根据奇偶判断就好了。
2.如果A > B。
首先考虑所有堆的石子数都小于$A + B$的情况,这样对于每一堆石头,一个人取过,另一个人就不能再取了,而且先手在任意一堆上只能操作1次,后手则可能操作多次。先去掉那些$<B$的堆,即两个人都不能取的堆。
如果剩下偶数堆,那么先手必败,因为先后手都能取走一半的堆。
如果剩下奇数堆,如果存在一些堆的石头数 $ < A $&& $ >= B $, 即只有后手能取,那么后手必胜,因为后手可以比先手多取一些堆。 接着考虑如果某一堆石头$>= 2 * B$,后手肯定会抢这堆石头,因为这堆时候允许它操作多次。如果不存在这样特殊的堆,那么先手可以比后手多取走一堆,先手胜。 如果只存在一个这样的堆,那么先手只要一开始就拿这一堆,同样可以胜利。否则后手一定可以拿到一个特殊的堆,那么后手的操作次数至少不会少于先手,后手胜。
再考虑石头数可以$>= A + B$的情况。我们称把所有堆的石子数mod $(A + B)$后的局面为约化后的局面,然后证明一个局面和它约化后的局面胜负情况是一样的。
证明:
如果约化后的局面后手必胜,那么显然原来的局面后手也必胜。因为后手只要采取下面的策略就可以获胜:如果先手取了$>= A + B$的堆,后手也跟着取那一堆,否则后手采取和约化后的局面对应的策略。
如果约化后的局面后手必败,那么约化后的局面,$>= 2 * B$的堆只有0个或1个,先手只要一上来就先取这样的堆,然后之后如果后手取了$>= A + B$的堆,先手就跟着他取,否则采取和约化后的局面对应的策略,这样就可以胜利了。
3. A < B. 枚举先手第一步取哪个,转化为上一种情况。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 100010 5 int v[MAXN]; 6 int x, y, z, tot; 7 8 void add(int t, int a, int b) 9 { 10 if (t < b) --tot; 11 12 if (t >= a) ++x; 13 if (t >= b && t < a) ++y; 14 if (t >= 2 * b) ++z; 15 } 16 17 void del(int t, int a, int b) 18 { 19 if (t < b) ++tot; 20 21 if (t >= a) --x; 22 if (t >= b && t < a) --y; 23 if (t >= 2 * b) --z; 24 } 25 26 int main() 27 { 28 int n, a, b; 29 scanf("%d %d %d", &n, &a, &b); 30 for (int i = 1; i <= n; ++i) 31 scanf("%d", &v[i]); 32 33 34 int flag = 0; 35 if (a == b) 36 { 37 int cnt = 0; 38 for (int i = 1; i <= n; ++i) 39 cnt += v[i] / a; 40 puts(cnt & 1? "Zenyk":"Marichka"); 41 } 42 else if (a > b) 43 { 44 x = y = z = 0, tot = n; 45 for (int i = 1; i <= n; ++i) 46 { 47 int t = v[i] % (a + b); 48 add(t, a, b); 49 } 50 flag |= (tot%2==0) || z >= 2 || y; 51 puts(!flag? "Zenyk":"Marichka"); 52 } 53 else 54 { 55 x = y = z = 0, tot = n; 56 for (int i = 1; i <= n; ++i) 57 { 58 int t = v[i] % (a + b); 59 if (t < a) --tot; 60 61 if (t >= b) ++x; 62 if (t >= a && t < b) ++y; 63 if (t >= 2 * a) ++z; 64 } 65 66 for (int i = 1; i <= n; ++i) 67 { 68 if (v[i] < a) continue; 69 del(v[i] % (a + b), b, a); 70 add((v[i] - a) % (a + b), b, a); 71 72 flag |= (tot%2==0) || z >= 2 || y; 73 add(v[i] % (a + b), b, a); 74 del((v[i] - a) % (a + b), b, a); 75 } 76 puts(flag? "Zenyk":"Marichka"); 77 } 78 return 0; 79 }
2016 Petrozavodsk Winter- Saratov SU Contest Problem B Game on Bipartite Graph(证明留坑)
http://codeforces.com/gym/100886
题意:
给出一个二分图,一开始棋子在左边,两人轮流玩,每次沿着边移动,移动后那条边删去,谁不能动谁就输了。 点数<=100.
题解:
考虑一个先手赢的局面,那么棋子的轨迹一定是左右左右。。。左右, 对于左边的点,如果它不是起点,那么轨迹中一定有偶数条边和它关联。如果是起点,一定有奇数条。
如果右边存在一个点集S,使得左边和S相关的点中,仅有起点度数为奇数,那么先手必胜,他只要每次只往S集合里的点走就好了。 这个条件是充要的,不过反过来还不清楚为什么是对的。。。 高斯消元求是否存在这样的点集就好了。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define N 100 5 int e[N][N], a[N][N]; 6 bool inset[N]; 7 8 void guass(int n, int m) 9 { 10 int line = 1, i, j, k, col[N]; 11 for (i = 1; i <= m && line <= n; ++i) 12 { 13 k = line; 14 for (j = line + 1; j <= n; ++j) 15 if (a[j][i]) k = j; 16 if (!a[k][i]) continue; 17 18 if (k != line) 19 { 20 for (j = i; j <= m + 1; ++j) 21 swap(a[k][j], a[line][j]); 22 } 23 24 for (j = line + 1; j <= n; ++j) 25 { 26 if (a[j][i]) 27 { 28 for (k = i; k <= m + 1; ++k) 29 a[j][k] ^= a[line][k]; 30 } 31 } 32 col[line++] = i; 33 } 34 --line; 35 for (i = line + 1; i <= n; ++i) 36 { 37 if (a[i][m + 1]) 38 { 39 return; 40 } 41 } 42 43 int ans[N] = {0}; 44 for (i = line; i >= 1; --i) 45 { 46 int s = a[i][m + 1]; 47 for (j = col[i] + 1; j <= m; ++j) 48 s ^= a[i][j] & ans[j]; 49 ans[col[i]] = inset[col[i]] = s; 50 } 51 } 52 53 int main() 54 { 55 int n, m, edges, v, x, y; 56 scanf("%d %d %d %d", &n, &m, &edges, &v); 57 while (edges--) 58 { 59 scanf("%d %d", &x, &y); 60 e[x][y]++; 61 } 62 for (int j = 1; j <= m; ++j) 63 { 64 for (int i = 1; i <= n; ++i) 65 a[i][j] = e[i][j] & 1; 66 } 67 a[v][m + 1] = 1; 68 guass(n, m); 69 70 while (true) 71 { 72 int t = -1; 73 for (int j = 1; j <= m; ++j) 74 if (e[v][j] && (t == -1 || inset[j])) 75 t = j; 76 if (t == -1) 77 { 78 puts("Player 2 wins"); 79 fflush(stdout); 80 break; 81 } 82 --e[v][t], v = t; 83 printf("%d\n", t); 84 fflush(stdout); 85 86 t = -1; 87 for (int i = 1; i <= n; ++i) 88 if (e[i][v]) t = i; 89 if (t == -1) 90 { 91 puts("Player 1 wins"); 92 fflush(stdout); 93 break; 94 } 95 96 int newv; 97 scanf("%d", &newv); 98 --e[newv][v], v = newv; 99 } 100 101 return 0; 102 }
XVIII Open Cup named after E.V. Pankratiev. GP of Romania Problem L Xormites(证明留坑)
http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=010391
题意:
给出一个自然数序列,两个人轮流,每次从两头拿一个数, 每个人的得分是拿的数异或起来,得分多的人赢。
题解:
如果一开始所有的数异或和如果为0,那么肯定平局。
否则异或和非零,考虑异或和最高位非0的位置。显然最终两个人的得分这一位一个是0,一个是1.
所以其它位可以丢掉,只考虑这一位。
如果N是偶数,将下标奇数位置染成白色,偶数位置染成黑色,先手可以取走所有白色,或者所有黑色,所以先手必胜。
如果N是奇数,那么先手必须要取一个1,否则根据N-1是偶数,剩下的根据上一条后手必胜。
依次check先手拿哪头的1.
先手拿走一个1后,剩下的数xor起来是0,之后后手不管拿什么,先手必须都要和他拿的一样,否则会使xor起来非0且剩下偶数个数,后手必胜。
接下来就是一个我还不知道怎么证明的结论(CF讨论里petr提到了这个结论但没有给出证明):
先手能每次模仿后手的取法,当且仅当剩下的序列是“S aabbccdd.... T”这样的形式,其中S和T是互为转置的01串。也就是说两头一段相等,中间相邻的相等。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 100010 5 typedef long long LL; 6 7 bool check(int l, int r, int a[]) 8 { 9 if (l > r) return true; 10 int ones = 0; 11 for (int i = l; i <= r; ++i) 12 ones += a[i] == 1; 13 if ((ones >> 1) & 1) return false; 14 15 while (l < r && a[l] == a[r]) ++l, --r; 16 for (int i = l; i <= r; i += 2) 17 if (a[i] ^ a[i + 1]) return false; 18 return true; 19 20 } 21 22 int solve() 23 { 24 int n, sum = 0; 25 static int a[MAXN]; 26 scanf("%d", &n); 27 for (int i = 1; i <= n; ++i) 28 scanf("%d", &a[i]), sum ^= a[i]; 29 if (sum == 0) return 0; 30 if (n % 2 == 0) return 1; 31 if (n == 1) return 1; 32 33 for (int i = 30; ; --i) 34 { 35 if ((sum >> i) & 1) 36 { 37 for (int j = 1; j <= n; ++j) 38 a[j] = (a[j] >> i) & 1; 39 break; 40 } 41 } 42 43 if (a[1] && check(2, n, a)) return 1; 44 if (a[n] && check(1, n - 1, a)) return 1; 45 return -1; 46 } 47 48 int main() 49 { 50 //freopen("in.txt", "r", stdin); 51 52 int T; 53 scanf("%d", &T); 54 while (T--) 55 { 56 int res = solve(); 57 if (res == 1) puts("First"); 58 else if (res == 0) puts("Draw"); 59 else puts("Second"); 60 } 61 62 return 0; 63 }
XVIII Open Cup named after E.V. Pankratiev. Grand Prix of Korea Problem J Game of Sorting
http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=010410
题目大意:
一个序列,每次只能从两头拿。谁操作完最后剩下的序列单调非降或者单调非增谁就赢。 Q个询问,每次问子区间[L, R]的结果。
题解:
1.如果一开始就单调,先手必败。
2.如果单调区间长度为区间长度-1, 那么先手必胜。
3.如果单调区间长度为区间长度-2:
3.a 如果[L + 1, R - 1]单调,显然先手必败。
3.b 如果[L, R - 2]单调, 显然先手必须先取A[L], 接着后手必须取A[L + 1]. 二分找到最多能两个两个取取多少次。
3.c 如果[L + 2, R]单调, 和3.b对称。
4. 如果单调区间长度 更小。
win[L, R] = !win[L, R - 1] | !win[L + 1, R] .
观察下图:
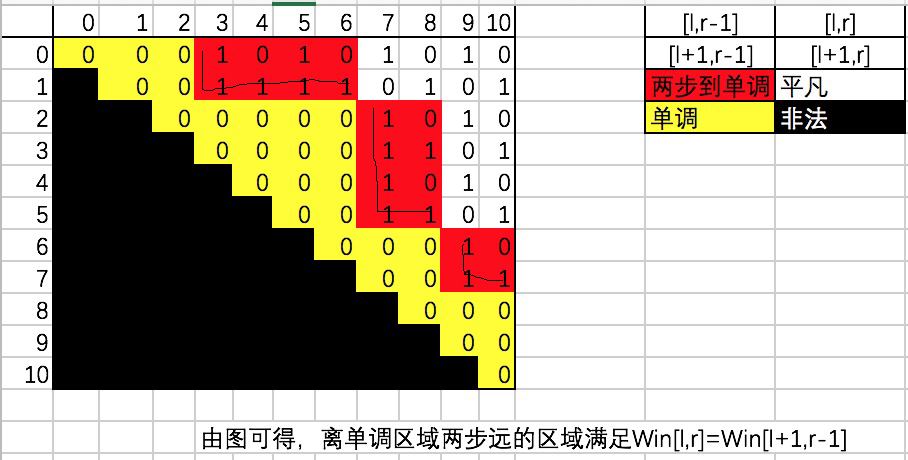
有win[L, R] = win[L + 1, R - 1]. 在上图中就是对角线元素相同, 单调区间长度为区间长度-2的情况实际上是为了求出一条对角线最左下角的那个。
根据这个,只要二分出可以确定的区间[L + k, R - k]再判断即可。
细节比较多的博弈题。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 1000010 5 typedef long long LL; 6 7 8 int a[MAXN], L[MAXN], f[MAXN], g[MAXN]; 9 10 int type(int l, int r) 11 { 12 if (l >= r) return 0; 13 if (L[r] <= l) return 0; 14 if (L[r] == l + 1 || L[r - 1] <= l) return 1; 15 if (L[r - 1] == l + 1) return 2; 16 if (L[r - 2] <= l) return 3; 17 if (L[r] <= l + 2) return 4; 18 return 5; 19 } 20 21 int solve(int l, int r) 22 { 23 int len = r - l + 1; 24 int kl, kr, kmid; 25 kl = 0, kr = r - l + 1; 26 while (kl < kr) 27 { 28 kmid = (kl + kr) >> 1; 29 if (type(l + kmid, r - kmid) == 5) kl = kmid + 1; 30 else kr = kmid; 31 } 32 l += kl; 33 r -= kl; 34 //cout << l << " " << r << " " << type(l + 1, r - 1) << endl; 35 if (L[r] <= l) return 0; 36 if (L[r] == l + 1 || L[r - 1] <= l) return 1; 37 if (L[r - 1] == l + 1) return 0; 38 else if (L[r - 2] <= l) 39 { 40 kl = 0, kr = len / 2; 41 while (kl < kr) 42 { 43 kmid = (kl + kr) >> 1; 44 if (type(l + kmid * 2, r) == type(l, r)) kl = kmid + 1; 45 else kr = kmid; 46 } 47 l += kl * 2; 48 return solve(l, r); 49 } 50 else 51 { 52 kl = 0, kr = len / 2; 53 while (kl < kr) 54 { 55 kmid = (kl + kr) >> 1; 56 if (type(l, r - kmid * 2) == type(l, r)) kl = kmid + 1; 57 else kr = kmid; 58 } 59 r -= kl * 2; 60 return solve(l, r); 61 } 62 } 63 int main() 64 { 65 //freopen("in.txt", "r", stdin); 66 67 int n, Q, l, r; 68 scanf("%d", &n); 69 for (int i = 1; i <= n; ++i) 70 scanf("%d", &a[i]); 71 L[1] = f[1] = g[1] = 1; 72 for (int i = 2; i <= n; ++i) 73 { 74 if (a[i] >= a[i - 1]) f[i] = f[i - 1]; 75 else f[i] = i; 76 if (a[i] <= a[i - 1]) g[i] = g[i - 1]; 77 else g[i] = i; 78 L[i] = min(f[i], g[i]); 79 } 80 scanf("%d", &Q); 81 while (Q--) 82 { 83 scanf("%d %d", &l, &r); 84 int res = solve(l, r); 85 if (res == 1) puts("Alice"); 86 else puts("Bob"); 87 } 88 return 0; 89 }
ps:
win[L, R] = win[L + 1, R - 1]的证明:
1. 如果win[L + 1, R - 1] = 0. 先手取L,后手取R,先手就输了;先手取R,后手取L,先手也是输。 所以win[L, R] = 0.
2. 如果win[L + 1, R - 1] = 1. 那么win[L + 2, R - 1] win[L + 1, R - 2]至少有一个等于1. 根据对称性假设win[L + 2, R - 1] = 1。 先手只要先取L, 然后如果后手取L + 1, 先手就取R, 如果后手取R, 先手就取L + 1. 所以先手可以胜利。 win[L, R] = 1.
Petrozavodsk Winter-2015. Jagiellonian U Contest Problem J. Game
http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=1456&locale_id=0
题目大意:一个序列,每次只能从两头拿。然后给出一些终止序列,即如果轮到某个人的时候,当前序列是终止序列,他就输了。 如果全被拿完,那么平局。问先手胜利还是后手胜利还是平局。(每个人如果他能获胜他就不会去平局)
题解:
1.首先有一个平局比较恶心。可以做两边,第一遍定义平局算先手胜利,第二遍定义平局算后手胜利。 如果第二遍先手胜利,那么先手肯定胜利。 否则先手肯定不能胜利,那么看他能不能平局。 只要看第一遍先手能不能胜利,能胜利就是平局,否则就是后手胜利。
2.定义win[L, R, draw = 0 or 1]表示只考虑[L, R]这一段,且平局算先手胜利(draw = 1)/ 失败(draw = 0) 的结果。 check(L, R)表示[L, R]这一段是否是终止序列。先考虑一些特殊的情况: 按顺序check下面每一条。
2.1 如果 check(L, R) = 1. win[L, R, draw] = 0.
2.2 如果L = R, win[L, R, draw] = draw.
2.3 如果check(L, R - 1) = 1 or check(L + 1, R) = 1。 那么显然先手可以获胜。
2.4 如果L + 1 = R, win[L, R, draw] = draw.
2.5 如果check(L + 2, R ) = 1. win[L, R, draw] = !win[L, R - 1, !draw]. 因为先手不能取L, 取L得话后手取L+1就凉了。 check(L, R - 2) = 1时同理有win[L, R, draw] = !win[L + 1, R, !draw].
2.6 如果check(L + 1, R - 1) = 1, win[L, R, draw] = 0. 因为先手随便取哪段,后手取另外一端就好了。
2.7 如果L + 2 = R, win[L, R, draw] = draw.
接下来是最重要的一条性质:win[L, R, draw] = win[L + 1, R - 1, draw]. 证明同上一题的ps部分。
1. 如果win[L + 1, R - 1] = 0. 先手取L,后手取R,先手就输了;先手取R,后手取L,先手也是输。 所以win[L, R] = 0.
2. 如果win[L + 1, R - 1] = 1. 那么win[L + 2, R - 1] win[L + 1, R - 2]至少有一个等于1. 根据对称性假设win[L + 2, R - 1] = 1。 先手只要先取L, 然后如果后手取L + 1, 先手就取R, 如果后手取R, 先手就取L + 1. 所以先手可以胜利。 win[L, R] = 1.
最后考虑如何求check(L, R)。 其实只要暴力检验每一个长度为R - L + 1的终止序列就好了,因为相同区间长度只会被check常数次。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define N 1000010 5 6 7 vector<vector<int> > lis[N]; 8 int n, m; 9 int a[N]; 10 11 12 bool check(int l, int r) 13 { 14 assert(l <= r); 15 int len = r - l + 1; 16 for (auto s: lis[len]) 17 { 18 int flag = 1; 19 for (int i = 0; i < len && flag; ++i) 20 if (s[i] ^ a[l + i]) flag = 0; 21 if (flag) return true; 22 } 23 return false; 24 } 25 26 int win(int l, int r, int draw) 27 { 28 assert(l <= r); 29 30 if (check(l, r)) return 0; 31 if (l == r) return draw; 32 33 if (check(l, r - 1) || check(l + 1, r)) return 1; 34 if (l + 1 == r) return draw; 35 36 if (check(l + 1, r - 1)) return 0; 37 if (check(l, r - 2)) return !win(l + 1, r, draw ^ 1); 38 if (check(l + 2, r)) return !win(l, r - 1, draw ^ 1); 39 if (l + 2 == r) return draw; 40 41 return win(l + 1, r - 1, draw); 42 43 } 44 45 void solve() 46 { 47 scanf("%d", &n); 48 for (int i = 0; i < n; ++i) 49 scanf("%d", &a[i]); 50 scanf("%d", &m); 51 52 53 while (m--) 54 { 55 int k, x; 56 scanf("%d", &k); 57 vector<int> s; 58 for (int i = 0; i < k; ++i) 59 scanf("%d", &x), s.push_back(x); 60 if (k < n) lis[k].push_back(s); 61 62 } 63 int win1 = win(0, n - 1, 1); 64 int win2 = win(0, n - 1, 0); 65 66 assert(!(win1 == 0 && win2 == 1)); 67 if (win1 & win2) puts("FIRST"); 68 else if (win1 | win2) puts("DRAW"); 69 else puts("SECOND"); 70 71 for (int i = 1; i <= n; ++i) lis[i].clear(); 72 73 } 74 75 int main() 76 { 77 int T; 78 scanf("%d", &T); 79 while (T--) 80 { 81 solve(); 82 } 83 return 0; 84 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号