最近做的一些题的简单题解

Codeforces Round #378 (Div. 2)

C：http://codeforces.com/contest/733/problem/C

题意：n个妖怪排成一队,如果某一秒钟 2个妖怪AB相邻,且A的体积大于B,那么A可以吃掉B,A的体积会增加B的体积。每一秒钟最多只会有一个妖怪吃掉另外一个妖怪。

给出最终剩下m个妖怪的体积,问是否存在一个吃的顺序,最终剩下的妖怪是这样的。 n,m<=500

题解：

首先最终剩下的每个妖怪的体积肯定是最开始连续的一些妖怪的体积之和,那么就可以确定最终剩下的每个妖怪是哪一段妖怪合起来的。所以只要考虑一段妖怪怎么合成一个妖怪。

我的方法是：如果这一段妖怪体积全相同,那么无解。否则,找到体积最大且能向左或者向右吃的某个妖怪,显然只要让它先吃掉一个妖怪让它体积变大一点,就可以吃所有剩下的妖怪的。总的时间复杂度O(n).

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <cstdlib>
#include <set>
#include <queue>
using namespace std;

#define X first
#define Y second
#define Mod 1000000007
#define N 1010
#define M 200010
typedef long long ll;
typedef pair<int,int> pii;

int n,m,t;
int a[N],b[N],ans1[N];
char ans2[N];

bool Solve(int l,int r)
{
    if (l==r) return true;
    int mx=0; bool flag=false;
    for (int i=l;i<=r;i++) mx=max(mx,a[i]);
    for (int i=l;i<=r;i++) if (a[i]!=mx) flag=true;
    if (!flag) return false;
    
    int s=0;
    for (int i=l;i<=r;i++)
    {
        if (a[i]==mx)
        {
            if (i>l && a[i-1]<mx) s=i;
        }
    }
    if (s!=0)
    {
        for (int i=1;i<=s-l;i++) t++,ans1[t]=s-i+1,ans2[t]='L';
        for (int i=1;i<=r-s;i++) t++,ans1[t]=l,ans2[t]='R';
        return true;
    }
    
    for (int i=l;i<=r;i++)
    {
        if (a[i]==mx)
        {
            if (i<r && a[i+1]<mx) s=i;
        }
    }
    for (int i=1;i<=r-s;i++) t++,ans1[t]=s,ans2[t]='R';
    for (int i=1;i<=s-l;i++) t++,ans1[t]=s-i+1,ans2[t]='L';
    return true;
}

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);

    scanf("%d",&n);
    for (int i=1;i<=n;i++) scanf("%d",&a[i]);
    scanf("%d",&m);
    for (int i=1;i<=m;i++) scanf("%d",&b[i]);
    for (int i=m,l,r=n,sum;i>=1;i--,r=l-1) 
    {
        for (l=r,sum=0;l && sum<b[i];l--) sum+=a[l]; l++;
        if (sum!=b[i]) {printf("NO\n"); return 0;}
        else if (!Solve(l,r)) {printf("NO\n");return 0;}
        if (i==1 && l!=1) {printf("NO\n"); return 0;}
    }
    printf("YES\n");
    for (int i=1;i<=t;i++) printf("%d %c\n",ans1[i],ans2[i]);
    return 0;
}

View Code

D:http://codeforces.com/contest/733/problem/D

题意：给出n个长方体,可以只选其中一个,或者选2个拼起来(有一个面相等的两个才能拼起来),然后从中得到一个最大的球。n<=100000

题解：

显然假设最终选的长方体(或者拼接成的长方体)的size是a*b*c,那么最大能得到的球的半径就是min(a,b,c)/2.

先处理掉不拼接的情况,对于2个拼起来的情况,假设选了2个a*b*c和a*b*d的长方体来拼,如果要最优,那么$c<=a\ ,\ c<=b\ ,\ d<=a\ ,\ d<=b$

因为球的半径受最短边的限制,对于一个长方体,如果拼上一个长方体后变优了,那么肯定要通过拼接改变最短边。

因此对于每个长方体,先让a>=b>=c,然后以a为第一关键字,b为第二关键字排序,那么能拼接的长方体在数组中肯定是连续的,搞一搞就可以求出最大值了。

总的复杂度O(nlogn)

#include <iostream>
#include <cstdio>
#include <cmath>
#include <queue>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <cstdlib>
#include <set>
using namespace std;

#define X first
#define Y second
#define Mod 1000000007
#define N 100010
#define M 200010
typedef long long ll;
typedef pair<int,int> pii;


int n,ans1,ans2,id,id1,id2;
int v[N][3];

struct node
{
    int x,y,z,d;
    bool operator < (const node &t)const
    {
        if (x==t.x)
        {
            if (y==t.y) return z<t.z;
            else return y<t.y;
        }
        else return x<t.x;
    }
}p[N];

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);

    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        scanf("%d%d%d",&v[i][0],&v[i][1],&v[i][2]);
        sort(v[i],v[i]+3);
        if (ans1<v[i][0]) id=i,ans1=v[i][0];
        p[i].x=v[i][2],p[i].y=v[i][1],p[i].z=v[i][0],p[i].d=i;
    }
    sort(p+1,p+n+1); 
    //for (int i=1;i<=n;i++) cout<<p[i].x<<" "<<p[i].y<<" "<<p[i].z<<endl;
    for (int i=1,j;i<=n;i=j+1)
    {
        j=i+1;
        while (j<=n && p[j].x==p[i].x && p[j].y==p[i].y) j++; j--;
        
        if (i!=j)
        {
            int tmp=min(p[j-1].z+p[j].z,p[j].x);
            tmp=min(tmp,p[i].y);
            if (tmp>ans2) ans2=tmp,id1=p[j].d,id2=p[j-1].d;
        }
    }
    if (ans1>=ans2) printf("1\n%d\n",id);
    else printf("2\n%d %d\n",id1,id2);
    
    return 0;
}

View Code

E：http://codeforces.com/contest/733/problem/E

题意：有n个台阶,每个台阶上写着'U'或者'D',如果一个人站在写着'U'的台阶上,就向上走,反之向下走。当人离开当前站的台阶后,台阶上的'U'会变成'D','D'会变成'U'. 从第1级台阶往下走,或者从第n级台阶往上走就离开了楼梯。求分别以每一级台阶为起点,多少步后走出楼梯。 n<=1000000

题解：假设起点是x,上面写着'D',那么人会不断向下走,直到碰到第一个'U',然后会返回x, 其结果是,把下方的第一个'U'变成了'D',然后改变了一次方向。接下来会一直往上走,直到碰到第一个'D',然后返回x,相当于把上方第一个'D'变成'U',然后改变方向。所以就很好搞了,有点周期性的味道,对于位置x,只要知道下方有多少个'U',这些'U'的坐标之和,上方有多少个'D',这些'D'的坐标之和,就可以计算出答案了。(最终是向上走出楼梯还是向下走出楼梯取决于下方'U'的个数,上方'U'的个数以及初始方向)

时间复杂度O(n).

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <cstdlib>
#include <set>
using namespace std;

#define X first
#define Y second
#define Mod 1000000007
#define N 1000010
#define M 200010
typedef long long ll;
typedef pair<int,int> pii;

int n,c1,c2;
int l[N],r[N];
ll s1[N],s2[N];
char str[N];

ll f1(int k,int pos){return (1ll*k*pos-(s1[c1]-s1[c1-k]))*2;}

ll f2(int k,int pos){return (s2[c2]-s2[c2-k]-1ll*k*pos)*2;}

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
    
    scanf("%d%s",&n,str+1);
    for (int i=n;i>=1;i--) if (str[i]=='D') r[++c2]=i;
    for (int i=1;i<=c2;i++) s2[i]=r[i]+s2[i-1];
    
    for (int i=1;i<=n;i++)
    {
        ll ans=0;
        if (str[i]=='U')
        {
            if (c2<=c1)
            {
                ans=n-i+1;
                ans+=f2(c2,i);
                ans+=f1(c2,i);
            }
            else
            {
                ans=i;
                ans+=f2(c1+1,i);
                ans+=f1(c1,i);
            }
            
            
            l[++c1]=i; s1[c1]=s1[c1-1]+i;
        }
        else
        {
            c2--;
            if (c1<=c2) 
            {
                ans=i;
                ans+=f1(c1,i);
                ans+=f2(c1,i);
            }
            else
            {
                ans=n-i+1;
                ans+=f1(c2+1,i);
                ans+=f2(c2,i);
            }
        }
        printf("%I64d%c",ans,i==n? '\n':' ');
    }
    return 0;
}

View Code

F: http://codeforces.com/contest/733/problem/F

题意： n个点m条边,每条边有2个值w_i和cost_i,即花cost_i的可以将w_i减去1. 一开始有S块钱,可以用来减少边的w_i,要使得最小生成树的边权和最小。 n,m<=200000

题解：假设最终选了一些边来构成最小生成树,那么肯定会选其中cost最小的一条边来降价。因此如果要降价,肯定是把钱都花在一条边上最优。先求MST,然后枚举降价的边,如果这条边在MST上,那么总的w减去相应的值就好。否则强制插入这条边<u,v>,必定会形成一个环,那么需要先删除MST上u->v之间边权最大的边。用树上倍增预处理即可。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <vector>
#include <set>
using namespace std;

#define N 200010
#define M 400010
typedef long long ll;
typedef unsigned long long ull;

struct Edge
{
    int x,y,z,w,id;
    bool flag;
    bool operator < (const Edge &t)const{return z<t.z;}
}e[N];

int n,m,tot,K;
int father[N],head[N],dep[N];
int f[N][19],g[N][19];
int to[M],val[M],nxt[M];


void Add_Edge(int x,int y,int z){to[tot]=y,nxt[tot]=head[x],val[tot]=z,head[x]=tot++;}

int Find(int x)
{
    if (x==father[x]) return x;
    father[x]=Find(father[x]);
    return father[x];
}

void Merge(int x,int y)
{
    x=Find(x),y=Find(y);
    if (x!=y) father[x]=y;
}

void Dfs(int x,int d)
{
    dep[x]=d; 
    for (int i=head[x],y;i!=-1;i=nxt[i])
    {
        y=to[i]; if (y==f[x][0]) continue;
        f[y][0]=x,g[y][0]=val[i]; Dfs(y,d+1);
    }
}

int Calc(int x,int y)
{
    int res=0;
    if (dep[x]<dep[y]) swap(x,y);
    for (int j=18;j>=0;j--) if ((1<<j)<=dep[x]-dep[y]) res=max(res,g[x][j]),x=f[x][j];
    if (x==y) return res;
    
    for (int j=18;j>=0;j--) if (f[x][j]!=f[y][j]) res=max(res,g[x][j]),res=max(res,g[y][j]),x=f[x][j],y=f[y][j];
    res=max(res,g[x][0]),res=max(res,g[y][0]);
    return res;
}

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
    
    ll ans=1ll<<60,sum=0,tmp;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=m;i++) scanf("%d",&e[i].z);
    for (int i=1;i<=m;i++) scanf("%d",&e[i].w);
    for (int i=1;i<=m;i++) scanf("%d%d",&e[i].x,&e[i].y),e[i].id=i;
    scanf("%d",&K); sort(e+1,e+m+1);
    for (int i=1;i<=n;i++) father[i]=i,head[i]=-1;
    
    for (int i=1;i<=m;i++)
    {
        int x=e[i].x,y=e[i].y,z=e[i].z;
        if (Find(x)!=Find(y))
        {
            Merge(x,y);

            sum+=e[i].z;
            e[i].flag=true; 
        
            Add_Edge(x,y,z);
            Add_Edge(y,x,z);
        }
    }
    Dfs(1,0);
    for (int j=1,h=2;h<=n;h<<=1,j++)
    {
        for (int i=1;i<=n;i++)
        {
            f[i][j]=f[f[i][j-1]][j-1];
            g[i][j]=max(g[i][j-1],g[f[i][j-1]][j-1]);
        }
    }
    int t;
    for (int i=1;i<=m;i++)
    {
        if (e[i].flag) tmp=sum-K/e[i].w;
        else
        {
            tmp=sum-Calc(e[i].x,e[i].y);
            tmp+=e[i].z-K/e[i].w;
        }
        if (tmp<ans) ans=tmp,t=i;
    }
    e[t].z-=K/e[t].w;
    printf("%I64d\n",ans);
    
    for (int i=1;i<=n;i++) father[i]=i;
    sort(e+1,e+m+1);
    for (int i=1;i<=m;i++) e[i].flag=false;
    for (int i=1;i<=m;i++)
    {
        int x=e[i].x,y=e[i].y,z=e[i].z;
        if (Find(x)!=Find(y))
        {
            Merge(x,y);
            e[i].flag=true; 
             printf("%d %d\n",e[i].id,e[i].z);
        }
    }

    return 0;
}

View Code

Canada Cup 2016

C：http://codeforces.com/contest/725/problem/C

像这样将A-Z放在2*13的格子里,相邻和对角的格子能连同. 比如下图中F和ERSTG都相邻。

ABCDEFGHIJKLM
NOPQRSTUVWXYZ

给出长度为27的字符串,保证A-Z都出现过,表示路径。

比如ABCDEFGHIJKLMNOPQRSGTUVWXYZ 表示从A到B到C最后一直到Z。

构造一种方法将A-Z放到2*13的格子里,使得这样的路径存在。

题解：比赛的时候漏掉了给出的字符串中保证A-Z都出现过这个条件,只会爆搜,于是T了...

字符串长度为27,且26个字母都出现过,那么肯定是只有一个字母出现了2次,其他出现了1次。

构造一： http://blog.csdn.net/qq_33199236/article/details/52915634

构造二：(官方题解)删掉第二次出现的字母,然后将剩下的26个字母顺时针放一圈,不断旋转这个圈总有一个时刻满足题意。

D：http://codeforces.com/contest/725/problem/D

题意：ACM现场赛有n支队伍,目前每支队伍有ti个气球,队伍的重量是wi。(气球越多排名越高) 你可以开挂把自己队伍的气球分一些给别的队伍,如果某个队伍的气球数大于重量,就会飞走(出局), 求你的队伍的可能最好排名。

题解：要提高自己的排名,肯定要把气球给排在自己前面的队伍,而且优先给容易飞走的队伍。因此维护一个优先队列,一开始把所有排在自己前面的队伍存进去,每次踢掉一只队伍,不断拿当前排名和最优排名比较。注意把气球给别的队伍之后可能会被后面的队伍超过,因此每次踢别人之后还要把超过自己的加入优先队列。

时间复杂度O(nlogn) 因为每个元素最多进入优先队列一次,出去一次。

Codeforces Round #377 (Div. 2)

D：http://codeforces.com/contest/732/problem/D

有n天m门课,第i门课需要用a_i天来复习,第i天可以参加d_i这门课的考试。每天可以参加一门课的考试或者复习一门课。问最少要多少天可以通过所有考试。 n,m<=100000

题解：考虑二分答案Mid,判断前Mid是否能完成所有考试的时候,假设这Mid天里有好多天可以考一门课,那么肯定放在最靠后的那一天来考。所以扫一遍,碰到没考试的天或者可以延后考的情况,就把当前空闲天数+1,碰到考试且不能延后,就把空闲天数减去需要的复习天数,如果不够肯定不可行。比赛的时候由于没有判断前Mid天一次也不能考某门课的情况,FST了。时间复杂度O(nlogn)

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <cstdlib>
#include <set>
using namespace std;

#define X first
#define Y second
#define Mod 1000000007
#define N 100010
#define M 200010
typedef long long ll;
typedef pair<int,int> pii;

int n,m;
int v[N],nxt[N],last[N],b[N];

bool Check(int Mid)
{
    int cnt=0,c=0;
    for (int i=1;i<=Mid;i++)
    {
        if (v[i]==0 || nxt[i]<=Mid) cnt++;
        else 
        {
            if (b[v[i]]>cnt) return false;
            cnt-=b[v[i]]; c++;
        }
    }
    return c==m;
}

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);

    scanf("%d%d",&n,&m);
    for (int i=0;i<=m;i++) last[i]=n+1;
    for (int i=1;i<=n;i++) scanf("%d",&v[i]);
    for (int i=n;i>=1;i--)
    {
        nxt[i]=last[v[i]];
        last[v[i]]=i;
    }
    for (int i=1;i<=m;i++) scanf("%d",&b[i]);
    
    int L=0,R=n,Mid;
    while (L<R)
    {
        Mid=(L+R)>>1;
        if (Check(Mid)) R=Mid;
        else L=Mid+1;
    }
    if (Check(L)) printf("%d\n",L);
    else printf("-1\n");
    
    return 0;
}

View Code

E：http://codeforces.com/contest/732/problem/F

题意：给出n点个m条无向边,要求给这些无向边定方向,r_i为定向之后从第i个点出发能到达的点的数目,要使得r_i的最小值最大。 n,m<=400000

题解：首先考虑缩点,找出所有桥,先去掉这些桥边,在每个块内做一次dfs,让dfs的方向就是边的方向,可以使得块内的所有点互相都能到达。接下来就是确定桥边的方向。

假设给桥边确定好了方向,缩点之后,成为一个有向无环图,那么肯定有一个点的出度为0(反证：如果不存在出度为0的点,图又是无环的,那么从一个点出发可以一直往下走下去,显然不对). 那么r_i的最小值肯定不能超过这个块的size了。于是我们可以构造一个方案：缩点之后可以看成一个树,以size最大的块为树的根,从上往下确定边的方向。这样就构造了一个答案为maxsize的解,显然不可能比这个解更加优。输出方案挺恶心...代码略丑时间复杂度O(n+m)

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <vector>
#include <set>
using namespace std;

#define N 400010
#define M 400010
typedef long long ll;
typedef unsigned long long ull;

int n,m,dfs_clock;
int dfn[N],low[N],id[N];
bool vis[N];
vector<int> g[N],g2[N];

struct Edge
{
    int x,y,rev;
    bool bridge;
    Edge(int _x=0,int _y=0):x(_x),y(_y){}
}e[M];

void Dfs(int x,int father)
{
    dfn[x]=low[x]=++dfs_clock;
    for (int y,i=0;i<g[x].size();i++)
    {
        y=e[g[x][i]].x==x? e[g[x][i]].y:e[g[x][i]].x;
        if (y==father) continue;
        
        if (!dfn[y]) Dfs(y,x),low[x]=min(low[x],low[y]);
        else low[x]=min(low[x],dfn[y]);
        if (low[y]>dfn[x]) e[g[x][i]].bridge=true;
    }
}

int Dfs2(int x,int father,int num)
{
    int cnt=1;  id[x]=num; vis[x]=true;
    for (int y,i=0;i<g[x].size();i++)
    {
        y=e[g[x][i]].x==x? e[g[x][i]].y:e[g[x][i]].x;
        if (y==father || e[g[x][i]].bridge) continue;
        if (!e[g[x][i]].rev) e[g[x][i]].rev= e[g[x][i]].y==x? 2:1;
        //cout<<num<<" "<<x<<" "<<y<<" "<<e[g[x][i]].rev<<" "<<e[g[x][i]].x<<" "<<e[g[x][i]].y<<endl;
        if (!vis[y]) cnt+=Dfs2(y,x,num);            
    }
    return cnt;
}

void Dfs3(int x,int father)
{
    for (int y,i=0;i<g2[x].size();i++)
    {
        y=id[e[g2[x][i]].x]==x? id[e[g2[x][i]].y]:id[e[g2[x][i]].x];
        if (y==father) continue;
        e[g2[x][i]].rev=id[e[g2[x][i]].x]==x? 2:1;
        Dfs3(y,x);
    }
}

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
    
    int x,y,cnt,mx=0,tot=0,rt;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        e[i]=Edge(x,y);
        g[x].push_back(i);
        g[y].push_back(i);
        e[i].bridge=false;
        e[i].rev=0;
    }
    Dfs(1,0);
    for (int i=1;i<=n;i++) if (!vis[i]) 
    {
        cnt=Dfs2(i,0,++tot);
        if (cnt>mx) mx=cnt,rt=id[i];
    }
    //for (int i=1;i<=m;i++) cout<<i<<" "<<e[i].bridge<<endl;
    for (int i=1;i<=m;i++) if (e[i].bridge)
    {
        x=id[e[i].x],y=id[e[i].y];
        g2[x].push_back(i);
        g2[y].push_back(i);
    }

    Dfs3(rt,0);
    printf("%d\n",mx);
    for (int i=1;i<=m;i++)
    {
        if (e[i].rev==2) printf("%d %d\n",e[i].y,e[i].x);
        else printf("%d %d\n",e[i].x,e[i].y);
    }
    
    return 0;
}

View Code

Codeforces Round #376 (Div. 2)

C：http://codeforces.com/contest/731/problem/C

题意：

有n双袜子,每双袜子有一个颜色.有m天,第i天要穿编号为li和ri的袜子,但是它们的颜色可能不同。

求最少改变多少双袜子的颜色能使得每天穿的袜子颜色一样。n,m<=200000

题解：利用并查集,可以求出最终哪些袜子的颜色必须一样。对于最终的每一个集合,找出其中颜色相同的最多的袜子,将整个集合的袜子的颜色染成这个颜色。

时间复杂度O(n)

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <cstdlib>
#include <set>
using namespace std;

#define X first
#define Y second
#define Mod 1000000007
#define N 200010
#define M 200010
typedef long long ll;
typedef pair<int,int> pii;

int n,m,k;
int c[N],father[N],cnt[N];
vector<int> g[N];

int Find(int x)
{
    if (father[x]==x) return x;
    int tmp,fa=x;
    while (fa!=father[fa]) fa=father[fa];
    while (x!=fa)
    {
        tmp=father[x];
        father[x]=fa;
        x=tmp;
    }
    return fa;
}

void Merge(int x,int y){x=Find(x),y=Find(y),father[x]=y;}

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
    
    int x,y,ans,mx;
    scanf("%d%d%d",&n,&m,&k); ans=n;
    for (int i=1;i<=n;i++) scanf("%d",&c[i]),father[i]=i;
    for (int i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        Merge(x,y);
    }
    for (int i=1;i<=n;i++) g[Find(i)].push_back(i);
    for (int i=1;i<=n;i++) if (father[i]==i)
    {
        int t;  mx=0; 
        for (int j=0;j<g[i].size();j++)
        {
            t=c[g[i][j]];
            cnt[t]++;
            mx=max(mx,cnt[t]);
        }
        for (int j=0;j<g[i].size();j++)
        {
            t=c[g[i][j]];
            cnt[t]--;
        }        
        ans-=mx;
    }
    printf("%d\n",ans);
    return 0;
}

View Code

D: http://codeforces.com/contest/731/problem/D

题意：

给出n个字符串,每个字符串里的元素是<=c的正整数。

每次可以将所有字符串里的每个元素+1, 如果那个数是c,就会变成1.

要求一个p,即进行p次操作后可以使得这n个字符串按字典序排序。 n<=500000,所有字符串的长度和<=1000000

题解：

考虑相邻的两个字符串S,T,设S和T从第i位开始不同,分别是x,y. 那么要使(x+p)%c < (y+p)%c p的解是1个或者2个区间.

这样最后就转化为求区间的交了,方法很多, 比如对于区间[L,R],可以将a[L]++ , a[R+1]--, 最后扫一遍就好。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;

#define N 1000010
int c;
int len[N],s[N];
vector<int> w[N];

void Add(int l,int r)
{
    if (l>r) return;
    //cout<<l<<" "<<r<<endl;
    s[l]++,s[r+1]--;
}

bool Solve(vector<int> &a,vector<int> &b)
{
    int n=a.size(),m=b.size(),x,y,d,t;
    
    for (int i=0;i<n && i<m;i++)
    {
        if (a[i]!=b[i])
        {
            x=a[i],y=b[i];
            d=x<y? y-x:c-(x-y);
            t=c-1-d;
            if (x>t) Add(c-x,c-x+t);
            else Add(0,t-x),Add(c-x,c-1);
            return true;
        }
    }
    if (n<=m) Add(0,c-1);
    return n<=m;
}

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    
    int n,x;
    scanf("%d%d",&n,&c);
    for (int i=1;i<=n;i++)
    {
        scanf("%d",&len[i]);
        for (int j=1;j<=len[i];j++) scanf("%d",&x),w[i].push_back(x-1);
    }
    for (int i=1;i<n;i++) 
    {
        //cout<<"num="<<i<<endl;
        if (!Solve(w[i],w[i+1]))
        {
            printf("-1\n");
            return 0;
        }
    }
    
    int now=0,ans; bool flag=false;
    for (int i=0;i<c;i++)
    {
        now+=s[i];
        if (now==n-1) flag=true,ans=i;
    }
    if (flag) printf("%d\n",ans);
    else printf("-1\n");
    
    return 0;
}

View Code

E：http://codeforces.com/contest/731/problem/E

题意：

有n个数,AB轮流玩游戏,从左边开始取数,每次可以至少要取走2个,将这些数加起来得到一个sum,取得人得到sum分,并把sum这个数放到最左边。最后只剩下一个数的时候游戏结束。 A先取,两个人的目标都是让自己的得分减去对方的得分尽可能大 ,并且都采取最优策略。问A最多能比B多多少分(可能是负数)。

题解：

可以发现任何状态都可以是将原来数列的前i个数合并后得到。

因此一个状态可以用当前第1个数是原来的前多少个数合并的结果来表示。

dp[i]表示将前i个数合并后先手比后手最多多多少分。我们要求的是dp[1].

dp[n]=0. dp[i]=max{S[k]-dp[k]} i<k<=n.

实现的时候可以保存S[k]-dp[k]的最大值,时间复杂度O(n)

define X first
#define Y second
#define Mod 1000000007
#define N 200010
#define M 200010
typedef long long ll;
typedef pair<int,int> pii;

int n;
int v[N];
ll S[N],dp[N];

int main()
{
    //freopen("in.in","r",stdin);
    //freopen("out.out","w",stdout);
    
    scanf("%d",&n);
    for (int i=1;i<=n;i++) scanf("%d",&v[i]),S[i]=S[i-1]+v[i];
    
    ll mx=S[n]; dp[n]=0;
    for (int i=n-1;i>=1;i--)
    {
        dp[i]=mx;
        mx=max(mx,S[i]-dp[i]);
    }
    printf("%I64d\n",dp[1]);
    
    return 0;
}

View Code

F: http://codeforces.com/contest/731/problem/F

题意：给出n个数,要求先选出某个数x, 然后选择一些数y,要求y是x的倍数,如果不是,需要将y减小成x的某个倍数, 使得最后的和最大。 n<=200000,a_i<=200000

题解：

话说这题放在F题的位置还是偏水了点。

先用个cnt[i]统计i出现多少次。枚举x, 那么x<=y<=2x-1 的y对答案的贡献都是x, 2x<=y<=3x-1贡献都是2x 依次类推。用个前缀和处理下就好了。

$\text{[math]}$

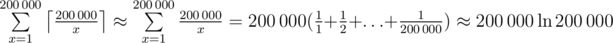
时间复杂度O(nlogn)

posted @ 2016-11-04 19:27 lzw4896s 阅读(222) 评论(0) 编辑收藏举报

刷新页面返回顶部

lzw4896s

最近做的一些题的 简单题解

公告

最近做的一些题的简单题解