[机器学习实战-Logistic回归]使用Logistic回归预测各种实例
[机器学习实战-Logistic回归]使用Logistic回归预测各种实例#
本实验代码已经传到gitee上,请点击查收!#
一、实验目的#
- 学习Logistic回归的基本思想。
- Sigmoid函数和Logistic回归分类器。
- 学习最优化算法--梯度上升算法、随机梯度上升算法等。
- 运用Logistic回归预测各种实例。
二、实验内容与设计思想#
实验内容#
- 基于Logistic回归和Sigmoid函数分类
- 基于最优化方法的最佳回归系数确定
- 示例1:从疝气病症预测病马的死亡率
- 示例2:从打斗数和接吻数预测电影类型(数据自制)
- 示例3:从心脏检查样本帮助诊断心脏病(数据来源于网络)
- 改进函数封装使不同的样本数据可以使用相同的函数封装
设计思想#
- Logistic回归的一般步骤:
- 收集数据:采用任意方法收集数据。
- 准备数据:由于需要进行距离计算,因此要求数据类型为数值型。另外,结构化数据格式则最佳
- 分析数据:采用任意方法对数据进行分析。
- 训练算法:大部分时间将用于训练,训练的目的是为了找到最佳的分类回归系数。
- 测试算法:一旦训练步骤完成,分类将会很快。
- 使用算法:首先,我们需要输入一些数据,并将其转换成对应的结构化数值;接着,基于训练好的回归系数就可以对这些数值进行简单的回归计算。判定它们属于哪个类别;在这之后,我们就可以输出的类别上做一些其他的分析工作。
三、实验使用环境#
- 操作系统:Microsoft Windows 10
- 编程环境:Python 3.6、Pycharm、Anaconda
四、实验步骤和调试过程#
4.1 基于Logistic回归和Sigmoid函数分类#
- 优点:计算代价不高,易于理解和实现。
- 缺点:容易欠拟合,分类精度可能不高。
- 使用数据类型:数值型和标称型数据。
Logistic回归算法只能用于预测结果只有两种情况(即要么0,要么1)的实例。而我们需要的函数则是能接收所有输入特征,最后预测出类别。且函数能稳定在某两个值之间,且能够平均分配,这里就引入了数学上的一个函数,即Sigmoid函数。
Sigmoid函数计算公式如下:
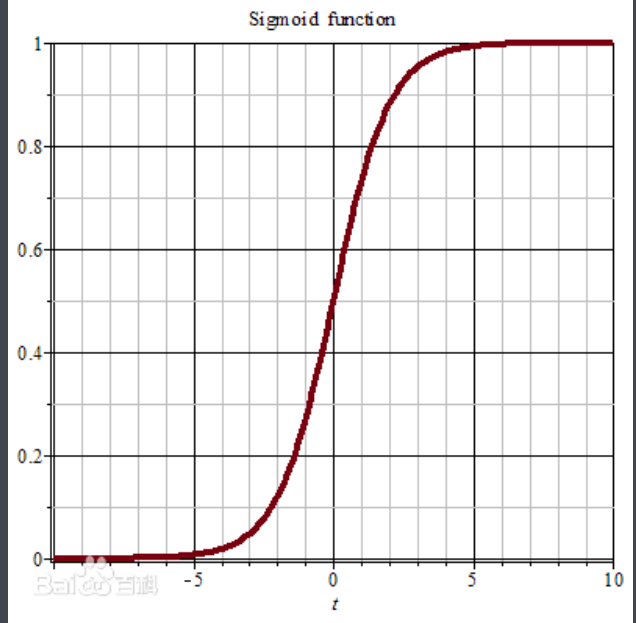
Sigmoid函数图像如下(来源:百度百科-Sigmoid函数):
Sigmoid函数特点描述:
当z值为0,Sigmoid函数值为0.5.随着z的不断增大,对应的Sigmoid值将逼近1;而随着z的减小,Sigmoid值将逼近与0。如果横坐标刻度足够大,那么纵观Sigmoid函数,它看起来很像一个阶跃函数。
而Sigmoid函数中的z值是需要经过下列计算的,为了实现Logistic回归分类器,我们可以在每一个特征上乘以一个回归系数,然后把所有的结果值相加,而这个相加的总和就是z值了。再将z值代入到Sigmoid函数中,可以得到一个0到1之间的数值,我们将任何大于0.5的数值归为1类,小于0.5的数值被归为0类。所以,Logistic回归可以被看做是一种概率估算。
在上面说明了z值的计算方法后,我们用公式来更直观地描述z值计算:
用向量的写法,上述公式可以写成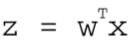 ,表示将这两个数值向量对应元素相乘起来然后全部加起来即是z值。其中
,表示将这两个数值向量对应元素相乘起来然后全部加起来即是z值。其中向量x是分类器的输入数据,即特征值数据;向量w是我们需要寻找的最佳系数,寻找最佳系数的目的是为了让分类器的结果尽可能的精确。
经过上面分析,Sigmoid函数公式最终形式可以写成下面这种形式:
4.2 基于最优化方法的最佳回归系数确定#
上面我们提到z值计算中,w的值是回归系数,而回归系数决定了预测结果的准确性,为了获取最优回归系数,我们需要使用最优化方法。最优化方法这里学习和使用两种:梯度上升算法和随机梯度上升算法(是对梯度上升算法的改进,使计算复杂度降低)。
4.2.1 梯度上升算法:#
算法思想:要找到某函数的最大值,最好的方法是沿着该函数的梯度方向探寻。
算法迭代公式:
其中:
4.2.2 测试算法:使用梯度上升算法找到最佳参数#
def loadDataSet():
"""
读取测试文件中的数据,拆分得到的每一行数据并存入相应的矩阵中,最后返回。
:return: dataMat, labelMat
dataMat: 特征矩阵
labelMat: 类型矩阵
"""
# 初始化特征列表和类型列表
dataMat = []
labelMat = []
# 打开测试数据,默认为读方式
fr = open("data/testSet.txt")
# 通过readLines()方法可以获得文件中的所有行信息
for line in fr.readlines():
# 将一行中大的信息先通过strip()方法去掉首尾空格
# 再通过split()方法进行分割,默认分割方式是空格分割
# 将分割好后的数据存入列表lineArr
lineArr = line.strip().split()
# 取出列表lineArr中的数据通过append方法插入到dataMat列表表中
# 这里为了方便计算,将第一列的值都设置为1.0
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
# 再取出文件中的最后一列的值作为类型值存入labelMat列表中
labelMat.append(int(lineArr[2]))
"""
列表中的append方法小结:
从上面两个列表添加元素的语句可以看出:
当我们需要添加一行数据时,需要加[],表示将插入一行数据。
当我们将数据直接插入到某一列的后面时,则不需要加[]。
且需要注意的是:如果一次要添加好几个元素时,必须有[],否则会报错。
"""
return dataMat, labelMat
def sigmoid(inX):
"""
sigmoid函数:α(z) = 1 / (1 + e^(-z))
:param inX: 函数中的参数z
:return: 返回函数计算结果
"""
return 1.0 / (1 + exp(-inX))
def gradAscent(dataMatIn, classLabels):
"""
梯度上升算法
:param dataMatIn: 特征值数组
:param classLabels: 类型值数组
:return: 返回最佳回归系数
"""
# 通过numpy模块中的mat方法可以将列表转化为矩阵
dataMatrix = mat(dataMatIn)
# transpose()方法是矩阵中的转置
labelMatrix = mat(classLabels).transpose()
# 通过numpy中大的shape方法可以获得矩阵的行数和列数信息
# 当矩阵是一维矩阵时,返回的是一个数的值
# 当矩阵是二维矩阵时,返回的是一个(1*2)的元组,元组第一个元素表示行数,第二个元素表示列数
m, n = shape(dataMatrix) # m = 100; n = 3
alpha = 0.001 # 步长
maxCycles = 500 # 迭代次数
# ones()属于numpy模块,函数功能是生成一个所有元素都为1的数组
# 这里是生成一个“n行1列”的数组,数组中每一个元素值都是1
weights = ones((n, 1))
# 循环迭代maxCycles次,寻找最佳参数
for k in range(maxCycles):
# dataMatrix * weights 是矩阵乘法
# 矩阵相乘时注意第一个矩阵的列数要和第二个矩阵的行数相同
# (m × n) * ( n × 1) = (m × 1) 括号中表示几行几列
# (100 × 3) * (3 × 1) = (100 × 1)
# 最后得到一个100行1列的矩阵
# 该矩阵运算结果为为sigmoid函数(α(z) = 1 / (1 + e^(-z)))中的z
# z的公式为:z = w0x0 + w1x1 + w2x2 + ... + wnxn
h = sigmoid(dataMatrix * weights)
# 计算真实类别与预测类别的差值
error = labelMatrix - h
# 按差值error的方向调整回归系数
# 0.01 * (3 × m) * (m × 1)
# 表示每一个列上的一个误差情况,最后得到x1,x2,xn的系数偏移量
# 矩阵乘法,最后得到一个更新后的回归系数
# 梯度上升算法公式:w:=w+α▽w f(w)
# 其中α是步长,▽w f(w)是上升方向
weights = weights + alpha * dataMatrix.transpose() * error
return array(weights)
输出:
if __name__ == '__main__':
dataMats, classMats = loadDataSet()
dataArr = array(dataMats)
weights = array(gradAscent(dataMats, classMats))
print(weights) # 输出最佳系数w的各个值
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
小结:
-
梯度上升算法核心函数是
gradAscent(dataMatIn, classLabels)函数,在该函数中不断迭代使得参数w不断优化,使得最终返回的参数最优。 -
上述的
sigmoid(inX)函数就是我们使用的Sigmoid函数公式,写成函数是因为下面我们会频繁的使用到这个函数,所以将该公式单独封装成一个函数。 -
loadDataSet()函数作用就是将我们收集到的数据读取出来,并且将读取出来的数据格式化存储到相应的数组中,最后返回供外界使用和分析。 -
这里小结一下列表中的
append()方法和extend()方法:if __name__ == '__main__': li = [] appendLi = [1, 2, 3] extendLi = [3, 4, 5] li.append(appendLi) print(li) li.extend(extendLi) print(li)输出:
[[1, 2, 3]]
[[1, 2, 3], 3, 4, 5]可以看到append()方法是将appendLi这个列表加入到li列表的新的一行,而extend()方法则是将extendLi列表中的数值取出来一个个接在li列表后面。
-
这里涉及到的numpy模块中的新函数(所谓新,是相对于我来说滴):
mat():将数组或则列表转化为矩阵- 矩阵中包含的方法:
transpose()方法是矩阵的转置。 - 矩阵相乘需要注意:第一个矩阵的列数需要和第二个矩阵的函数相同。
-
line.strip().split()用法:可以看到这里是对字符串的切割,字符串line先通过strip()方法去掉了首尾的空格,在通过split()方法进行默认空格切割。两种方法一气呵成,不用分成两不写。
4.2.3 分析数据:画出决策边界#
def plotBestFit(dataArr, labelMat, weights):
"""
画出决策边界
:param dataArr: 特征值数组
:param labelMat: 类型数组
:param weights: 最佳回归系数
:return:
"""
# 通过shape函数获得dataArr的行列数,其中[0]即行数
n = shape(dataArr)[0]
# xCord1和yCord1是类型为1的点的x和y坐标值
xCord1 = []
yCord1 = []
# xCord2和yCord1是类型为0的点的x和y坐标值
xCord2 = []
yCord2 = []
# 特征数组的每一行和类型数组的没每一列一一对应
for i in range(n):
# 当类型为1时,
# 将特征数组中的指定行的1和2两个下标下的值分别作为x轴和y轴的值
if int(labelMat[i]) == 1:
xCord1.append(dataArr[i, 1])
yCord1.append(dataArr[i, 2])
# 当类型为0时,
# 将特征数组中的指定行的1和2两个下标下的值分别作为x轴和y轴的值
else:
xCord2.append(dataArr[i, 1])
yCord2.append(dataArr[i, 2])
# figure()操作时创建或者调用画板
# 使用时遵循就近原则,所有画图操作是在最近一次调用的画图板上实现。
fig = plt.figure()
# 将fig分成1×1的网格,在第一个格子中加载ax图
# 参数111表示“1×1网格中的第1个表格”
# 如果参数是211则表示“2行1列的表格的中的第一个表格”
# 第几个表格的计算顺序为从左到右,从上到下
ax = fig.add_subplot(111)
# 设置散点图参数
# 前两个参数xCord1,yCord1表示散点对应的x和y坐标值
# s=30表示散点大小为30
# c='red'表示散点颜色为红色
# marker='s'表示散点的形状,这里是正方形
ax.scatter(xCord1, yCord1, s=30, c='red', marker='s')
# 同上说明
ax.scatter(xCord2, yCord2, s=30, c='green')
# 生成一个[-3.0, 3.0]范围中间隔每0.1取一个值
x = arange(-3.0, 3.0, 0.1)
# y相对于x的函数
"""
这里的y是怎么得到的呢?
从dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
可得:w0*x0+w1*x1+w2*x2 = z
x0最开始就设置为1,x2就是我们画图的y值,x1就是我们画图的x值。
所以:w0 + w1*x + w2*y = 0
→ y = (-w0 - w1 * x) / w2
"""
y = (-weights[0] - weights[1] * x) / weights[2]
# 画线
ax.plot(x, y)
# 设置x轴和y轴的名称
plt.xlabel('x1')
plt.ylabel('x2')
# 展示图像
plt.show()
输出:
if __name__ == '__main__':
dataMats, classMats = loadDataSet()
dataArr = array(dataMats)
weights = array(gradAscent(dataMats, classMats))
plotBestFit(dataArr, classMats, weights) # 调用该函数话决策边界
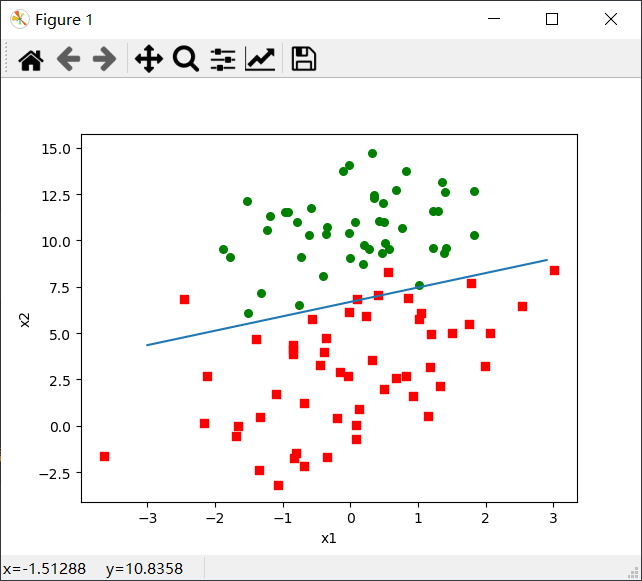
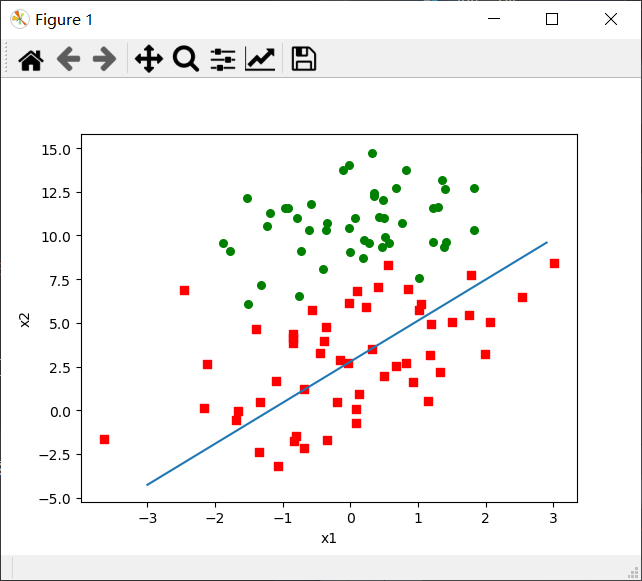
输出图如下:
小结:
-
观察上面的图示,可以看出这个分类结果相当不错,只错分了三四个点。
-
画图方法小结:(箭头表示赋值)
- 调用画板→fig:plt.figure() 方法。(plt是画图工具包我们取的别名)
-
划分画板→ax:fig.add_subplot(111)方法,其中111表示1*1的画板中的第1个画板。
- 画图:画曲散点图用ax.sctter()方法,画曲线图用ax.plot()方法
-
设置坐标名称:plt.xlabel('x1')和plt.ylabel('x2'),这里设置x轴名称为x1,y轴名称为x2。
- 显示图画:plt.show()方法。
-
但是尽管该例子很小且数据集很小,求最佳系数时需要大量的计算(300次乘法)。对于几百个左右的数据集合还可以,但是如果是10亿个样本和成千上万的特征,那么这个计算方法的复杂度太高了,甚至可能出不来最佳系数。所以下面引入随机梯度上升算法。
4.2.4 训练算法:随机梯度上升#
def stocGradAscent0(dataMatrix, classLabels):
"""
随机梯度上升算法
:param dataMatrix: 特征值矩阵
:param classLabels: 类型数组
:return: 最佳系数weights
"""
# m = 100,n = 3
m, n = shape(dataMatrix)
alpha = 0.01
weights = ones(n)
print(weights)
# 循环迭代m次,即100次
for i in range(m):
# (1 × 3) * (1 × 3) = (1 × 3)
# 数组相乘,两个数组的每个元素对应相乘
# 最后求和
# z = w0x0 + w1x1 + wnxn
# 在将z代入sigmoid函数进行计算
h = sigmoid(sum(dataMatrix[i] * weights))
# 计算实际结果和测试结果之间的误差,按照差值调整回归系数
error = classLabels[i] - h
# 通过梯度上升算法更新weights
weights = weights + alpha * error * dataMatrix[i]
return weights
使用上面的plotBestFit(dataArr, labelMat, weights)函数分析该算法。
输出:
if __name__ == '__main__':
dataMats, classMats = loadDataSet()
dataArr = array(dataMats)
weights = array(stocGradAscent0(dataArr, classMats))
plotBestFit(dataArr, classMats, weights)
小结:
- 通过图示可以看出,随机梯度上升算法错分了三分之一的样本。
- 随机梯度上升算法与梯度上升算法很类似,但是有一些区别:
- 后者的变量h和误差error都是向量,而前者则全是一个数值;
- 前者没有矩阵转换的过程,所有变量的数据类型都是Numpy,效率上会较后者快。
- 因为经过比较此时的随机梯度算法错分了三分之一的样本,我们通过下面的改进来优化一下该算法。
改进后的随机梯度上升算法代码如下:
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
"""
改进后的随机梯度上升算法
:param dataMatrix: 特征值矩阵
:param classLabels: 类型数组
:param numIter: 迭代次数,设置默认值为150
:return: 最佳系数weights
"""
m, n = shape(dataMatrix)
# 创建与列数相同矩阵,所有元素都为1
weights = ones(n)
# 随机梯度,循环默认次数为150次,观察是否收敛
for j in range(numIter):
# 产生列表为[0, 1, 2 ... m-1]
dataIndex = list(range(m))
for i in range(m):
# i和j不断增大,导致alpha不断减小,单上衣不为0,
# alpha会随着迭代不断的减小,但永远不会减小到0,因为后面还有一个常数项0.01
alpha = 4 / (1.0 + j + i) + 0.01
# 产生一个随机在0-len()之间的值
# random.uniform(x, y)方法将随机生成一个实数,他在[x, y]范围内,x<=y。
randIndex = int(random.uniform(0, len(dataIndex)))
# sum(dataMatrix[randIndex]*weights)是为了求z值
# z = w0x0 + w1x1 + ... + wnxn
h = sigmoid(sum(dataMatrix[randIndex] * weights))
# 计算实际结果和测试结果之间的误差,按照差值调整回归系数
error = classLabels[randIndex] - h
# 通过梯度上升算法更新weights
weights = weights + alpha * error * dataMatrix[randIndex]
# 删除掉此次更新中用到的特征数据
del(dataIndex[randIndex])
return weights
输出:
if __name__ == '__main__':
dataMats, classMats = loadDataSet()
dataArr = array(dataMats)
weights = array(stocGradAscent1(dataArr, classMats))
plotBestFit(dataArr, classMats, weights)
小结:
- 这里增加了3处代码来进行改进:
- 一方面,alpha在每次迭代的时候都会再进行调整。另外,虽然alpha会随着迭代次数不断减小,但永远不会减小到0,这是因为调整时还存在一个常数项。必须这样做的原因是为了保证多次迭代后新数据仍然具有一定的影响。
- 第二处改进,通过随机选取样本来更新回归系数。这种方法每次随机从列表中选取一个值,更新完系数后删除掉该值(再进行下一次迭代)。
- 第三就是该算法还增加了第三个参数,传入迭代的次数,默认值为150.
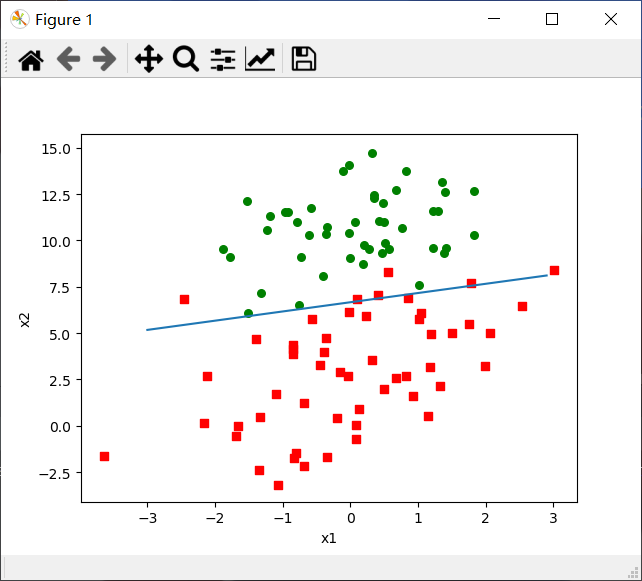
- 在看此时分析数据得到的划分图,此时划分只错分了几个样本数据,所以该优化后的随机梯度算法满足我们需求,且数据量大的时候不用进行矩阵变化,效率也比较高。
4.3 示例1:从疝气病症预测病马的死亡率#
这里我们将使用Logistic回归来预测患有疝气病症的马的存活问题。这里的数据包含299个训练样本和67个测试样本。其中我们通过21中特征值(每个特征代表什么我们可以不用关心)来进行预测患有疝病的马的存活率。1表示存活,0表示死亡。
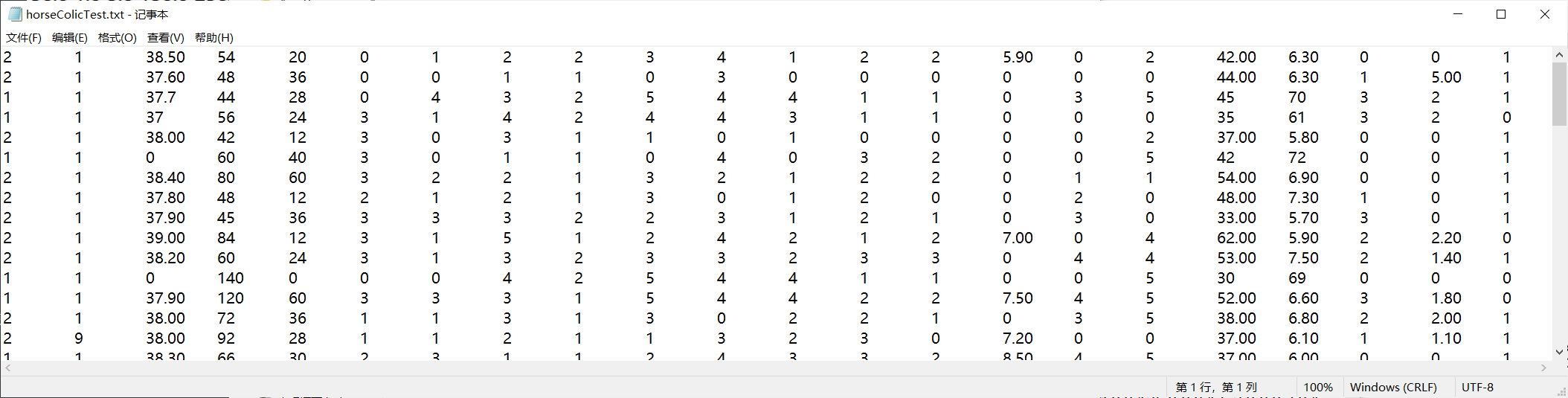
训练样本horseColicTraining.txt展示:
测试样本horseColicTest.txt展示:
测试算法:用Logistic回归进行分类
def classifyVector(inX, weights):
"""
使用梯度上升算法获取到的最优系数来计算测试样本中对应的Sigmoid值。
其中Sigmoid值大于0.5返回1,小于0.5返回0.
:param inX: 特征数组
:param weights: 最优系数
:return: 返回分类结果,即1或0
"""
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def colicTest():
"""
测试回归系数算法的用于计算疝气病症预测病马的死亡率的错误率。
这里运用的随机梯度算法来获取最佳系数w1,w2,...,wn
:return: 返回此次测试的错误率
"""
# 以默认只读方式打开训练数据样本和测试数据样本
frTrain = open('data/horseColicTraining.txt')
frTest = open('data/horseColicTest.txt')
trainingSet = []
trainingLabels = []
# 读取训练数据样本的每一行
for line in frTrain.readlines():
# 去掉首尾空格,并按tab空格数来切割字符串,并将切割后的值存入列表
currLine = line.strip().split('\t')
lineArr = []
# 将21个特征值依次加入到lineArr列表汇总
for i in range(21):
lineArr.append(float(currLine[i]))
# 再将lineArr列表加入到二维列表trainingSet列表中
trainingSet.append(lineArr)
# 将类型值依次接到trainingLabels这个列表的末尾行
trainingLabels.append(float(currLine[21]))
# 使用上面写的改进的随机梯度算法求得最佳系数,用于下面分类器使用区分类型
trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 300)
errorCount = 0
numTestVec = 0.0
# 读取测试数据的每一行
for line in frTest.readlines():
# 测试数据数加1
numTestVec += 1.0
# 去掉首尾空格,并以tab空格数切割字符串,并将切割后的值存入列表
currLine = line.strip().split('\t')
lineArr = []
# 将21个特征值依次加入到特征列表lineArr中
for i in range(21):
lineArr.append(float(currLine[i]))
# 通过上面计算得到的最佳系数,使用分类器计算lineArr这些特征下的所属的类型
if int(classifyVector(array(lineArr), trainWeights)) != int(currLine[21]):
# 如果分类器得到结果和真实结果不符,则错误次数加1
errorCount += 1
# 通过遍历获得的所有测试数据量和错误次数求得最终的错误率
errorRate = float(errorCount) / numTestVec
# 输出错误率
print("测试结果的错误率为:{:.2%}".format(errorRate))
# 返回错误率,用于计算n次错误率的平均值
return errorRate
def multiTest():
"""
多次测试算法的错误率取平均值,以得到一个比较有说服力的结果。
:return:
"""
numTests = 10
errorSum = 0.0
# 通过10次的算法测试,并获得10次错误率的总和
for k in range(numTests):
errorSum += colicTest()
# 通过错误率总和/10可以求得10次平均错误率并输出
print("10次算法测试后平均错误率为:{:.2%}".format(errorSum/float(numTests)))
输出:
if __name__ == '__main__':
multiTest()
测试结果的错误率为:29.85%
测试结果的错误率为:32.84%
测试结果的错误率为:35.82%
测试结果的错误率为:40.30%
测试结果的错误率为:34.33%
测试结果的错误率为:46.27%
测试结果的错误率为:32.84%
测试结果的错误率为:37.31%
测试结果的错误率为:29.85%
测试结果的错误率为:50.75%
10次算法测试后平均错误率为:37.01%
小结:
classifyVector(inX, weights)函数,是以最佳回归系数和特征向量作为输入来计算最终对应的Sigmoid值。如果Sigmoid值大于0.5,函数返回1,否则返回0。注意:这个函数后面其他实例也会经常用到,因为这个函数相当于一个分类器,可以获取到最终的预测结果。colicTest()函数,是用于打开测试集和训练测试集,并对数据进行格式化处理的函数,函数最终放回测试的错误率。multiTest()函数,其功能是调用10次colicTest()函数并求结果的平均值。为了使最终错误率更有说服力。- 从上面的结果可以看到10次迭代后的平均错误率为37.01%。事实上,这个结果并不差,因为样本数据中实际上有30%的数据缺失。当然,如果调整colicTest()的迭代次数和stochGradAscent1()中的步长,平均错误率可以降到20%左右。
- 当然后面如果我们有某些特征值需要判断,并使用该算法预测时,我们只需再增加一个输入各特征值的函数,然后调用classifyVector(inX, weights)函数,就可以预测出某些特征下疝病马是否会死亡。
4.4 示例2:从打斗数和接吻数预测电影类型(数据自制)#
从kNN算法里面的小例子得到启发,使用打斗数和接吻数这两个特征最终预测得到的电影类型只有两种:爱情片和动作片。所以符合Logistic回归算法的使用标准。
特征说明:打斗数、接吻数
类型说明:1表示动作片;0表示爱情片
自制数据代码展示:
# !/usr/bin/python3
# -*- coding: utf-8 -*-
# @Time : 2020/4/26 17:21
# @Author : zjw
# @FileName: generateData.py
# @Software: PyCharm
# @Blog :https://www.cnblogs.com/vanishzeng/
from numpy import *
def generateSomeData(fileName, num):
trainFile = open(fileName, "w")
for i in range(num):
fightCount = float(int(random.uniform(0, 101)))
kissCount = float(int(random.uniform(0, 101)))
if fightCount > kissCount:
label = 1 # 表示动作片
else:
label = 0 # 表示爱情片
trainFile.write(str(fightCount) + "\t" + str(kissCount) + "\t" + str(float(label)) + "\n")
trainFile.close()
if __name__ == '__main__':
generateSomeData("data/movieTraining.txt", 200)
generateSomeData("data/movieTest.txt", 100)
自制数据思路:通过随机生成打斗数和接吻数(数量在100以内),判断当打斗数大于接吻数时为动作片,记为1;当接吻数大于打斗数时为爱情片,记为0。并将数据写入相应的txt文件中。这里生成了200个训练样本和100个测试样本。最后,还经过对生成的样本数据,进行手动修改几个类别,以达到更加实际现实的样本数据。
样本展示:
测试算法:使用Logistic回归预测电影类别(关键代码展示)
def classifyVector(inX, weights):
"""
使用梯度上升算法获取到的最优系数来计算测试样本中对应的Sigmoid值。
其中Sigmoid值大于0.5返回1,小于0.5返回0.
:param inX: 特征数组
:param weights: 最优系数
:return: 返回分类结果,即1或0
"""
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def movieTest():
"""
使用Logistic回归算法测试判断电影类别的错误率。
:return: 错误率
"""
trainFile = open("data/movieTraining.txt")
testFile = open("data/movieTest.txt")
trainSet = []
trainLabels = []
for line in trainFile.readlines():
lineArr = line.strip().split('\t')
trainSet.append([float(lineArr[0]), float(lineArr[1])])
trainLabels.append(float(lineArr[2]))
trainWeights = stocGradAscent1(array(trainSet), trainLabels, 500)
errorCount = 0
allTestCount = 0
for line in testFile.readlines():
allTestCount += 1
lineArr = line.strip().split('\t')
eigenvalue = [float(lineArr[0]), float(lineArr[1])]
if classifyVector(eigenvalue, trainWeights) != float(lineArr[2]):
errorCount += 1
errorRate = float(errorCount)/float(allTestCount)
print("错误率为:{:.2%}".format(errorRate))
return errorRate
def multiTest():
"""
多次测试算法的错误率取平均值,以得到一个比较有说服力的结果。
:return:
"""
numTests = 10
errorSum = 0.0
# 通过10次的算法测试,并获得10次错误率的总和
for k in range(numTests):
errorSum += movieTest()
# 通过错误率总和/10可以求得10次平均错误率并输出
print("10次算法测试后平均错误率为:{:.2%}".format(errorSum/float(numTests)))
输出:
if __name__ == '__main__':
multiTest()
错误率为:11.00%
错误率为:6.00%
错误率为:5.00%
错误率为:6.00%
错误率为:5.00%
错误率为:10.00%
错误率为:4.00%
错误率为:7.00%
错误率为:14.00%
错误率为:11.00%
10次算法测试后平均错误率为:7.90%
小结:
- 这里测试算法的思路和上面的思路基本一致,只是对一些函数中的内容进行小修小补。
- 因为这里的数据是自制的,且特征数量只有两个,制作规则比较简单,且手动修改的类别不多,所以最终得到的错误率并不高,算法的测试结果是令人满意的。
4.5 示例3:从心脏检查样本帮助诊断心脏病(数据来源于网络)#
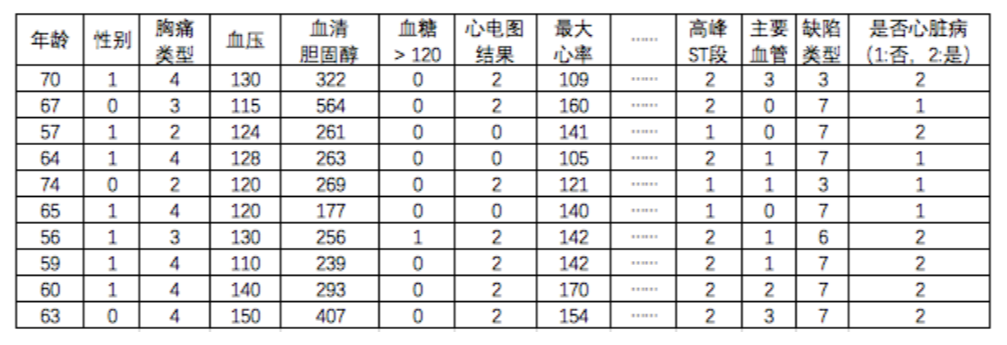
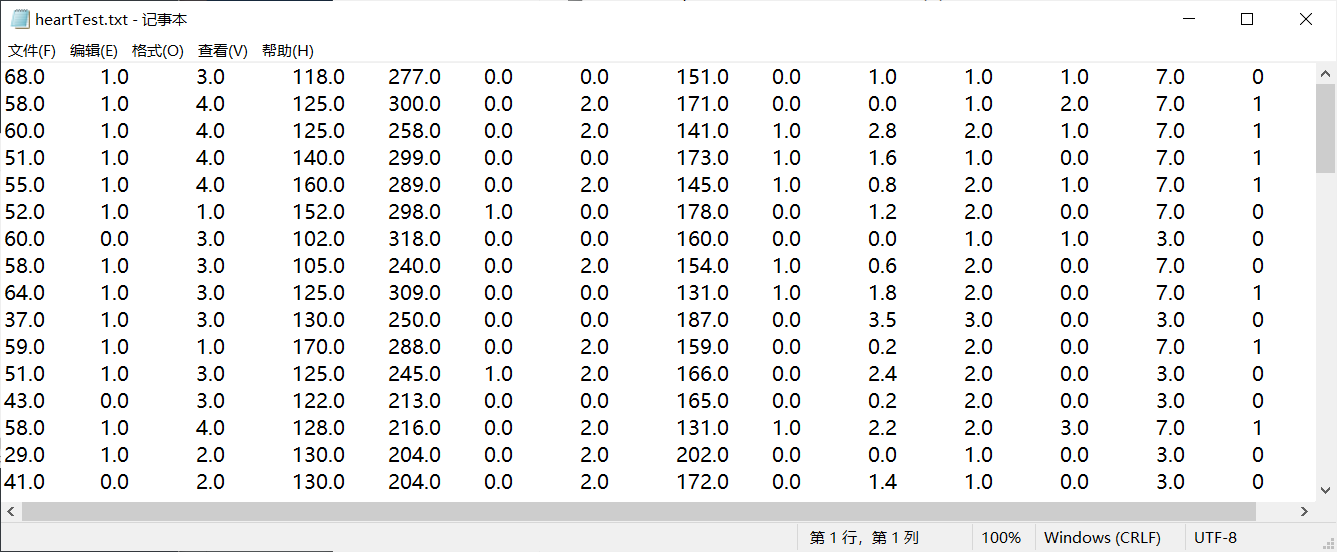
在这个例子中我们使用到一批心脏检查样本数据(数据来源于网络:Statlog (Heart) Data Set),这里我将获取到的270个样本数据分成两部分,一部分作为训练样本(heartTraining.txt)有200个样本数据,一部分作为测试样本(heartTest.txt)有70个样本数据。数据各列的特征(有13个特征)和是否为心脏病如下图所示:
注:这里中间有些特征没有标明,但这并不影响我们对数据的操作。
这里为了使数据便于后面的操作,我将数据集中最后一列数据进行了修改,原来是1表示否,2表示是;修改后1表示是,0表示否。
重构数据集的代码如下:
# !/usr/bin/python3
# -*- coding: utf-8 -*-
# @Time : 2020/4/29 9:54
# @Author : zjw
# @FileName: modifyDataFile.py
# @Software: PyCharm
# @Blog :https://www.cnblogs.com/vanishzeng/
def modifyData(fileName):
file = open(fileName, 'r')
allStr = []
for line in file.readlines():
arr = line.strip().split(' ')
if arr[13] == '1':
arr[13] = '0'
else:
arr[13] = '1'
s = ''
for i in range(14):
s += arr[i] + '\t'
s += '\n'
allStr.append(s)
file.close()
newFile = open(fileName, 'w')
newFile.writelines(allStr)
newFile.close()
if __name__ == '__main__':
modifyData('data/heartTest.txt')
modifyData('data/heartTraining.txt')
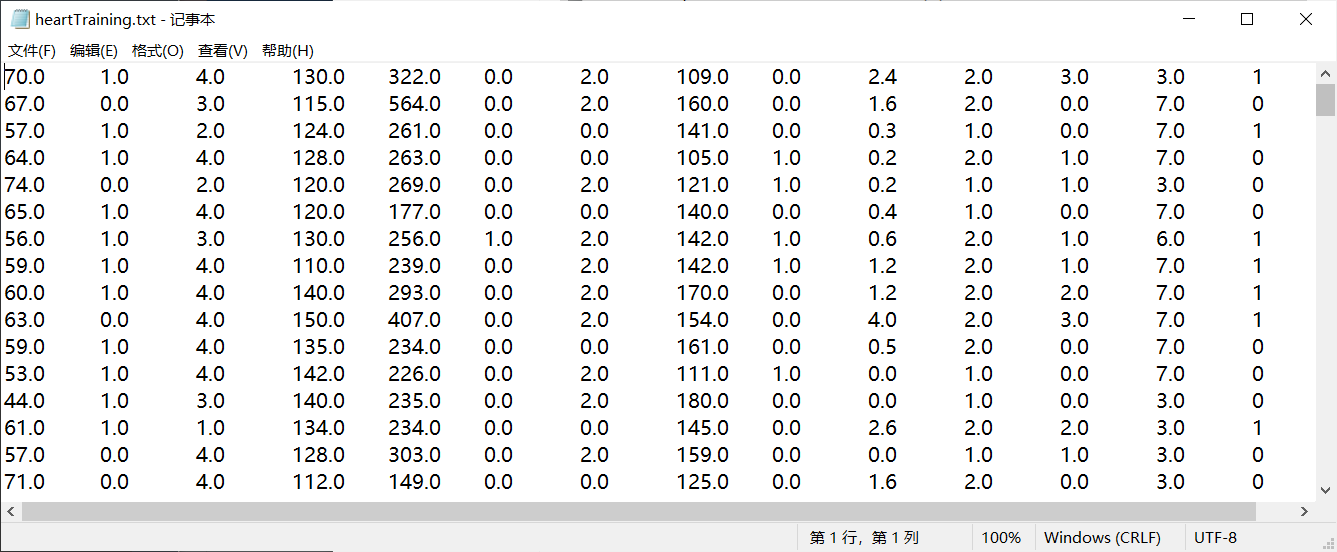
重构思路:将文本文件中的数据都读取出来,然后进行切割,将数据中的最后一列中的值通过if判别进行替换。并将修改好后的列表转化为一个个字符串,存入到allStr这个总列表中。最后再以写的方式打开文件,通过writelines()方法一次性将allStr列表写入文件中。
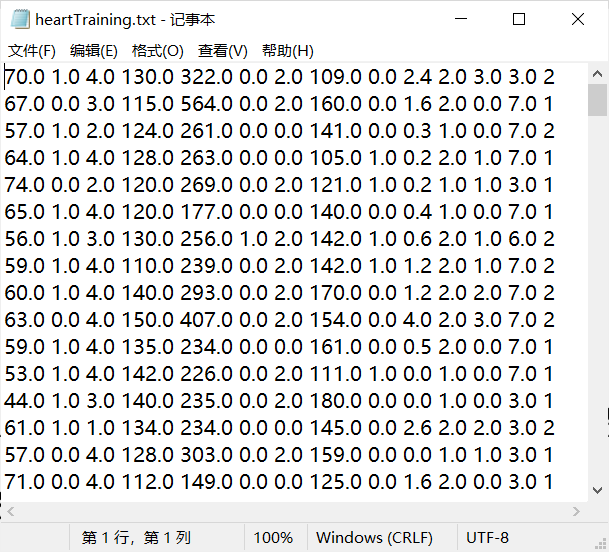
重构后的文件数据集:
测试算法:使用Logistic回归预测是否为心脏病(关键代码展示)
def classifyVector(inX, weights):
"""
使用梯度上升算法获取到的最优系数来计算测试样本中对应的Sigmoid值。
其中Sigmoid值大于0.5返回1,小于0.5返回0.
:param inX: 特征数组
:param weights: 最优系数
:return: 返回分类结果,即1或0
"""
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def heartTest():
"""
使用Logistic回归算法诊断心脏病的错误率。
:return:错误率
"""
trainFile = open("data/heartTraining.txt")
testFile = open("data/heartTest.txt")
trainSet = []
trainLabels = []
for line in trainFile.readlines():
lineArr = line.strip().split(' ')
temArr = []
for i in range(13):
temArr.append(float(lineArr[i]))
trainSet.append(temArr)
trainLabels.append(float(lineArr[13]))
trainWeights = stocGradAscent1(array(trainSet), trainLabels, 100)
errorCount = 0
allTestCount = 0
for line in testFile.readlines():
allTestCount += 1
lineArr = line.strip().split(' ')
eigenvalue = []
for i in range(13):
eigenvalue.append(float(lineArr[i]))
if classifyVector(eigenvalue, trainWeights) != float(lineArr[13]):
errorCount += 1
errorRate = float(errorCount) / float(allTestCount)
print("错误率为:{:.2%}".format(errorRate))
return errorRate
def multiTest():
"""
多次测试算法的错误率取平均值,以得到一个比较有说服力的结果。
:return:
"""
numTests = 10
errorSum = 0.0
# 通过10次的算法测试,并获得10次错误率的总和
for k in range(numTests):
errorSum += heartTest()
# 通过错误率总和/10可以求得10次平均错误率并输出
print("10次算法测试后平均错误率为:{:.2%}".format(errorSum/float(numTests)))
输出:
if __name__ == '__main__':
multiTest()
错误率为:18.57%
错误率为:17.14%
错误率为:15.71%
错误率为:31.43%
错误率为:24.29%
错误率为:12.86%
错误率为:21.43%
错误率为:12.86%
错误率为:32.86%
错误率为:22.86%
10次算法测试后平均错误率为:21.00%
小结:
- 可以看到测试算法的错误率为21%,是一个还不错的结果。因为这次得到的数据的特征值较多,且特征值之间也有所差别。可以通过增加迭代次数,以及调整步长进一步减低错误率。
- 在数据处理方面,从三个实例可以看出,基本上是一致的,知识因为特征值数量的不同,以及读取文件的不同,导致代码上有略微的区别。测试Logistic算法的大致思路都是一致的,测试算法思想:
- 读取训练样本中的数据,进行格式化处理;
- 将格式化处理后的数据传入随机梯度上升算法函数中,获取到最佳参数。
- 再读取测试样本中的数据,进行格式化处理后,调用分类器函数(传入样本特征和最佳参数),可以预测出最终特征。与测试数据中的实际特征进行比较,计算出错误次数。
- 最终通过错误次数/测试样本总数求出错误率。
- 为了使试验结果具有说服力,使用了多次求解错误率取平均值的方法。
- 经过上面的分析,我们可以看到在测试算法时,我们用到了基本一致的步骤,所以想到写几个函数,可以将这些步骤统一起来,通过传入某些参数来实现对不同特征数据的分析和预测。
4.6 改进函数封装使不同的样本数据可以使用相同的函数封装#
改进函数展示:
def dataTest(trainFileName, testFileName, numOfFeatures):
"""
函数功能:测试回归算法预测数据样本的错误率。
函数伪代码:
1. 读取训练样本中的数据,进行格式化处理;
2. 将格式化处理后的数据传入随机梯度上升算法函数中,获取到最佳参数。
3. 再读取测试样本中的数据,进行格式化处理后,调用分类器函数(传入样本特征和最佳参数),可以预测出最终特征。与测试数据中的实际特征进行比较,计算出错误次数。
4. 最终通过错误次数/测试样本总数**求出错误率。
:param trainFileName: 训练样本的文件路径/文件名
:param testFileName: 测试样本的文件路径/文件名
:param numOfFeatures: 样本所包含的特征数量
:return:
"""
trainFile = open(trainFileName)
testFile = open(testFileName)
trainSet = []
trainLabels = []
for line in trainFile.readlines():
lineArr = line.strip().split('\t')
temArr = []
for i in range(numOfFeatures):
temArr.append(float(lineArr[i]))
trainSet.append(temArr)
trainLabels.append(float(lineArr[numOfFeatures]))
trainWeights = stocGradAscent1(array(trainSet), trainLabels, 200)
errorCount = 0
allTestCount = 0
for line in testFile.readlines():
allTestCount += 1
lineArr = line.strip().split('\t')
eigenvalue = []
for i in range(numOfFeatures):
eigenvalue.append(float(lineArr[i]))
if classifyVector(eigenvalue, trainWeights) != float(lineArr[numOfFeatures]):
errorCount += 1
errorRate = float(errorCount) / float(allTestCount)
print("错误率为:{:.2%}".format(errorRate))
return errorRate
def multiTest1(trainFileName, testFileName, numOfFeatures):
"""
多次测试算法的错误率取平均值,以得到一个比较有说服力的结果。
:return:
"""
numTests = 10
errorSum = 0.0
# 通过10次的算法测试,并获得10次错误率的总和
for k in range(numTests):
errorSum += dataTest(trainFileName, testFileName, numOfFeatures)
# 通过错误率总和/10可以求得10次平均错误率并输出
print("10次算法测试后平均错误率为:{:.2%}".format(errorSum/float(numTests)))
输出:
if __name__ == '__main__':
print("示例1:示例1:从疝气病症预测病马的死亡率")
multiTest1('data/horseColicTraining.txt', 'data/horseColicTest.txt', 21)
print("\n示例2:从打斗数和接吻数预测电影类型")
multiTest1('data/movieTraining.txt', 'data/movieTest.txt', 2)
print("\n示例3:从心脏检查样本帮助诊断心脏病")
multiTest1('data/heartTraining.txt', 'data/heartTest.txt', 13)
示例1:从疝气病症预测病马的死亡率
错误率为:32.84%
错误率为:29.85%
错误率为:29.85%
错误率为:37.31%
错误率为:29.85%
错误率为:34.33%
错误率为:31.34%
错误率为:29.85%
错误率为:29.85%
错误率为:31.34%
10次算法测试后平均错误率为:31.64%示例2:从打斗数和接吻数预测电影类型
错误率为:14.00%
错误率为:6.00%
错误率为:14.00%
错误率为:3.00%
错误率为:6.00%
错误率为:11.00%
错误率为:5.00%
错误率为:11.00%
错误率为:5.00%
错误率为:5.00%
10次算法测试后平均错误率为:8.00%示例3:从心脏检查样本帮助诊断心脏病
错误率为:20.00%
错误率为:22.86%
错误率为:17.14%
错误率为:22.86%
错误率为:18.57%
错误率为:18.57%
错误率为:35.71%
错误率为:22.86%
错误率为:35.71%
错误率为:18.57%
10次算法测试后平均错误率为:23.29%
小结:
- 通过函数封装后,就可以直接传入相应的文件名和特征数即可测试不同的样本。解决了上面的代码冗余。
- 函数封装的思路主要是对上面写的测试函数进行重构,重构的位置有两个地方:
- 将colicTest()、movieTest()、heartTest()三个函数统一为
dataTest(trainFileName, testFileName, numOfFeatures)这个函数,增加了三个参数的目的是,原来三个函数中的不同的地方就是不同的文件和不同的特征数量,所以以参数的形式传递进来,即使有所不同,但是以函数内参数形式调用即可实现相同的功能。 - 将原来的multiTest()函数重构为
multiTest1(trainFileName, testFileName, numOfFeatures)这个函数,也是增加了和上面同样的三个参数,主要是因为在这个函数中要调用dataTest()这个函数,所以需要需要通过multiTest1这个函数间接帮忙传递参数。
- 将colicTest()、movieTest()、heartTest()三个函数统一为
- 通过该函数封装后,后面当我们需要测试新的数据使,只要告诉我文件所在位置和文件名,以及数据的特征数量,我就可以调用multiTest1()函数很快的计算出错误率,无需再写新的函数进行测试,极大的提高了效率。
五、实验总结#
-
Logistic回归算法的目的是寻找一个非线性函数Sigmoid的最佳拟合参数,求解过程可以使用最优化算法来完成。
-
最优化算法中,最常用的是梯度上升算法。梯度上升算法可以简化为效率比较高的随机梯度上升算法。
-
改进后的随机梯度上升算法的效果和梯度上升算法效果相当,但是占用更少的计算资源且效率更高。
-
Sigmoid函数:
-
函数封装很重要,可以解决代码冗余问题,此外也可以提高开发效率,不必每次一有新数据,就要重新写新的函数来满足要求。好的代码封装,后续只要调用相应的函数就可以完成指定的目标。
-
numpy相关函数:
- mat():将数组或列表转为矩阵形式。
- mat.transpose():矩阵转置
六、参考资料#
- 《机器学习实战》 Peter Harrington (作者) 李锐 , 李鹏 , 曲亚东 , 王斌 (译者) 第2章 k-近邻算法
- 预测心脏病的数据来源:http://archive.ics.uci.edu/ml/datasets/Concrete+Compressive+Strength
- 机器学习代码实战:使用逻辑回归帮助诊断心脏病
- Sigmoid函数
- 【机器学习笔记1】Logistic回归总结
版权声明:欢迎转载=>请标注信息来源于 Vanish丶博客园

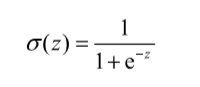
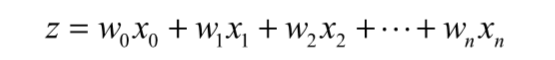
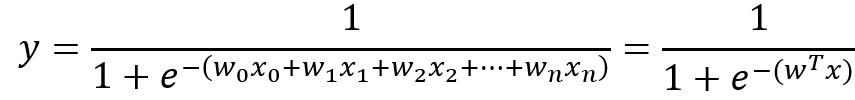
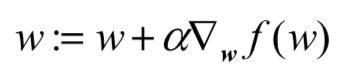
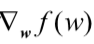
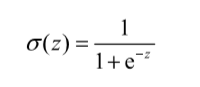



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek 解答了困扰我五年的技术问题
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 用 C# 插值字符串处理器写一个 sscanf
· Java 中堆内存和栈内存上的数据分布和特点
· 开发中对象命名的一点思考
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· DeepSeek 解答了困扰我五年的技术问题。时代确实变了!
· 本地部署DeepSeek后,没有好看的交互界面怎么行!
· 趁着过年的时候手搓了一个低代码框架
· 推荐一个DeepSeek 大模型的免费 API 项目!兼容OpenAI接口!