DS博客作业07--查找

1.本周学习总结

1.思维导图

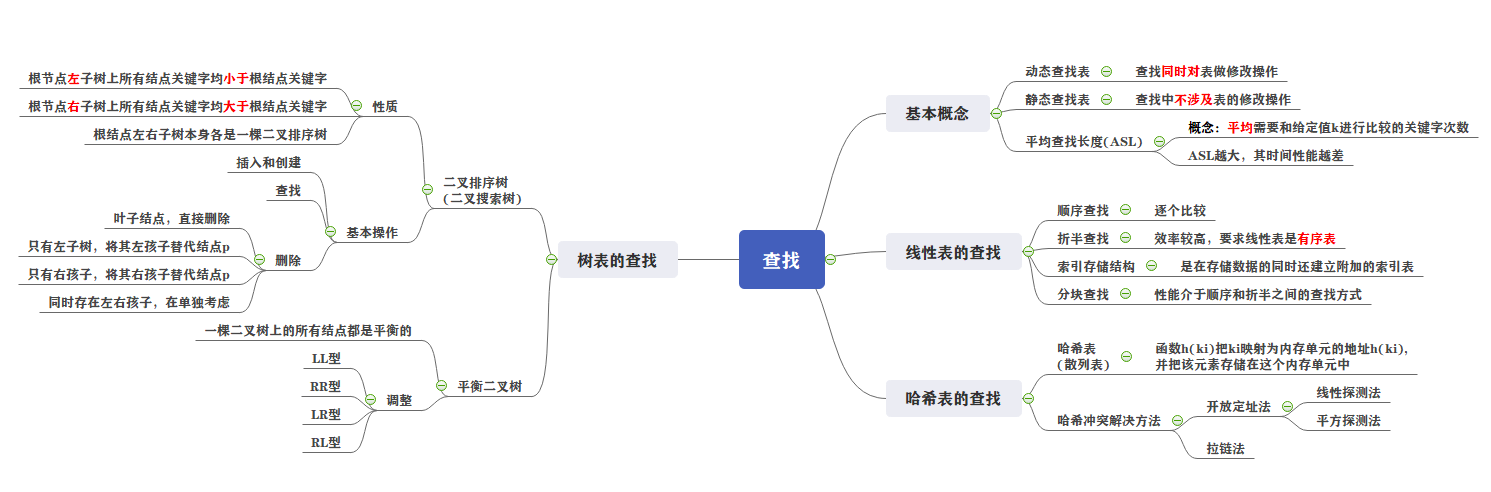
2.谈谈你对查找运算的认识及学习体会。

1.查找这一章主要要接触和熟练二叉排序树和哈希查找；
2.在二叉排序树中要重点学习删除操作，其有四种不同情况的删除情况；且二叉树中有引申出平衡二叉树和B树，平衡二叉树主要要了解他的调整过程，而B树要了解他的建树原则以及插入删除的过程；
3.在哈希查找中则学习了开放定址法的线性探测法和平方探测法以及需要除留余数法辅助建表，还有拉链法；拉链法处理冲突简单且无堆积现象，删除较易实现。
4.学会计算各种查找算法在成功和不成功情况下的的ASL。

2.PTA实验作业

2.1.题目1：6-2 是否二叉搜索树 (25 分)

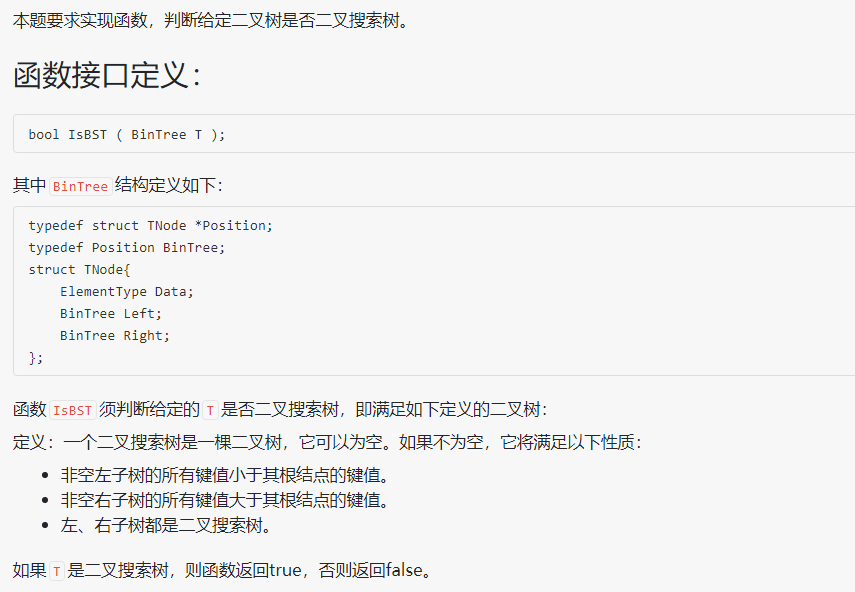
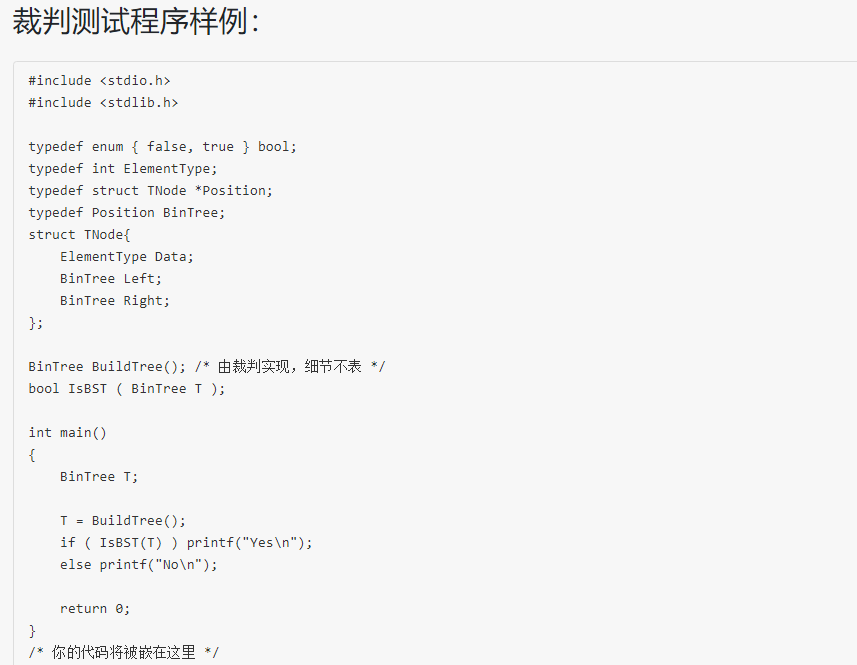
2.1.1设计思路（伪代码）

法一：通过中序遍历将二叉树的数据存入数组中，因为搜索二叉树中序遍历结点值是从小到大排列的，所以可以通过该方法判断是否为搜索二叉树。
//函数外创建数组num用于存结点关键字
//定义整型i为0开始记录地址位置
bool IsBST(BinTree T)
if T不为空 do
    //中序遍历,并将结点关键字依次存入数组num中
end if
for j=0 to i-1 do j++
    判断数组中上一个数是否比下一个数大
    小的话则错误
    返回false
end for
放回true

法二：遍历二叉树判断各个结点是否满足二叉搜索树的特点，若某个节点的左子树的最右结点的关键字值比该节点大，或右子树的最左结点关键字比该节点小，则为错误的二叉搜索树。
bool IsBST(BinTree T)
定义BinTree型的结点p
若树为空则返会true
若树的左右结点都为空，则返回true
p=T->Left
if p不为空 do
    while p->Right不为空 do
        p=p->Right
    end while //找到左子树的最右结点
    if p->Data>T->Data do 
        返回false
    end if 
end if
p=T->Right
//同理判断右子树的最左结点
分别遍历左子树和右子树判断正误

2.1.2代码截图

• 法一：

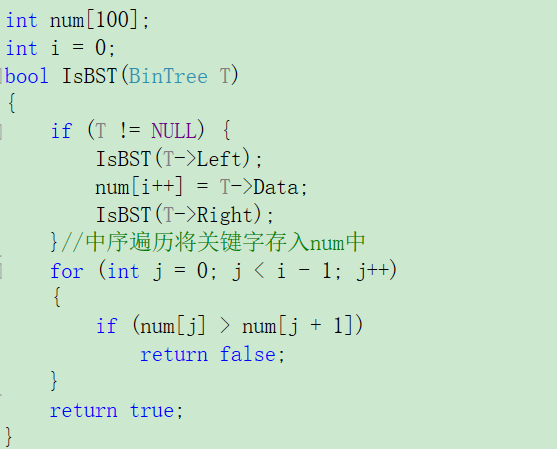
• 法二：

2.1.3本题PTA提交列表说明。

• Q1：使用法一是部分正确；
• A1：主要是在中序遍历时没有将值存入数组中，而只是单独的数组在自增，增加赋值之后即可；
• Q2：法二时判断正确的情况一直出现运行超时的情况；
• A2：因为有部分代码题目省略了，所以只能通过观察来解决错误，发现在赋值左右子树后用了while语句判断p是否为空的情况，导致正确的时候，出不了该while语句，从而导致超时，将其改成if即可。

2.2.题目2：6-4 jmu-ds-哈希表操作集 (15 分)

2.2.1设计思路（伪代码）

• 整体思路：采用除留取余法和线性探测法，将数据插入到哈希表中，在利用线性探测法查找元素。

void InsertHT(HashTable ha, int &n, KeyType k, int p)//哈希表插入数据
定义整型loc表示地址
定义整型counts记录查找次数
loc=k%p//除留余数法取哈希地址
if ha[loc].count等于0 do //此单元空闲可以插入
    给该单元赋关键字的值，并赋查找次数为1
else 
    while ha[loc].count!=0 do//说明该单元不为空，用线性探测法找空闲单元
        counts 递增
        loc=(loc+1)%p//线性探测法的数学递推公式
    end while
    counts加一//找到之后也算一次
    给该单元赋关键字的值，并赋查找次数为counts
end if
//---------分割线---------
void CreateHT(HashTable ha, KeyType x[], int n, int m, int p)  //创建哈希表
for i=0 to m do i++
    将哈希表中的所有哈希单元的查找次数都修改成零
end for
for i=0 to n do i++
    插入函数一次插入各个元素
end for
//---------分割线-----------
int SearchHT(HashTable ha, int p, KeyType k)	//在哈希表中查找关键字k
定义整型loc表示地址
loc=k%p//除留余数法取哈希地址
if 该查找地址的count查找次数为0 do //该位置为空时,说明该查找关键字不存在哈希表中
    返回-1
else 
    没有查找到的次数递增
    while 1 do 
         loc=(loc+1)%p//线性探测法的数学递推公式
         没有查找到的次数递增
        if 该查找地址的count查找次数为0 do
            返回-1
        end if
        if 哈希地址中的值和查找值相等 do
            返回该地址
        end if
    end while
end if     

2.2.2代码截图

2.2.3本题PTA提交列表说明。

• Q1：出现查找超时的情况；
• A1：用测试数据调试查找不到的元素，发现在程序一直卡在搜索的while(1)语句中，在看调试的一些数据，发现每个哈希地址中count都为1，表明哈希地址为满，所以不可能有查找不到的情况。经过调试后发现是在给所有哈希中count赋值零时，将哈希长度弄错为n，实际上是m。
• Q2：答案错误；
• A2：理解错误查找失败的查找次数的情况，全局变量定义的uns_count就是用来计算查找不成功的查找次数，添加到不成功的判断条件下即可成功。

2.3.题目3：7-2 航空公司VIP客户查询 (25 分)

2.3.1设计思路（伪代码）

声明一个map容器且对应类型都是long long的名称为vip
声明一个迭代器ster
定义整型变量IDNum存省份证号
定义字符型变量tail存身份证最后一位
定义distance存里程数
输入n,k//n代表n组数，k代表最低里程
while n-- do
    输入IDNum，tail,distance
    若tail为x则将IDNum置为负数
    iter为IDNum在map中的位置
    if 此IDNum不在vip中 do
        若distance小于最低里程k，则置为k
        将IDNum和distance的对应存入vip中
    else do    //IDNum存在
        若distance小于最低里程k，则置为k
        在该用户拥有的里程数基础上加上distance
    end if
end while
输入m
while m-- do//查找身份证所包含的里程数
    输入IDNum和tail
    若tail为x则将IDNum置为负数
    找IDNum在vip中的位置
    找到输出里程数，找不到输出No Info
end while

2.3.2代码截图

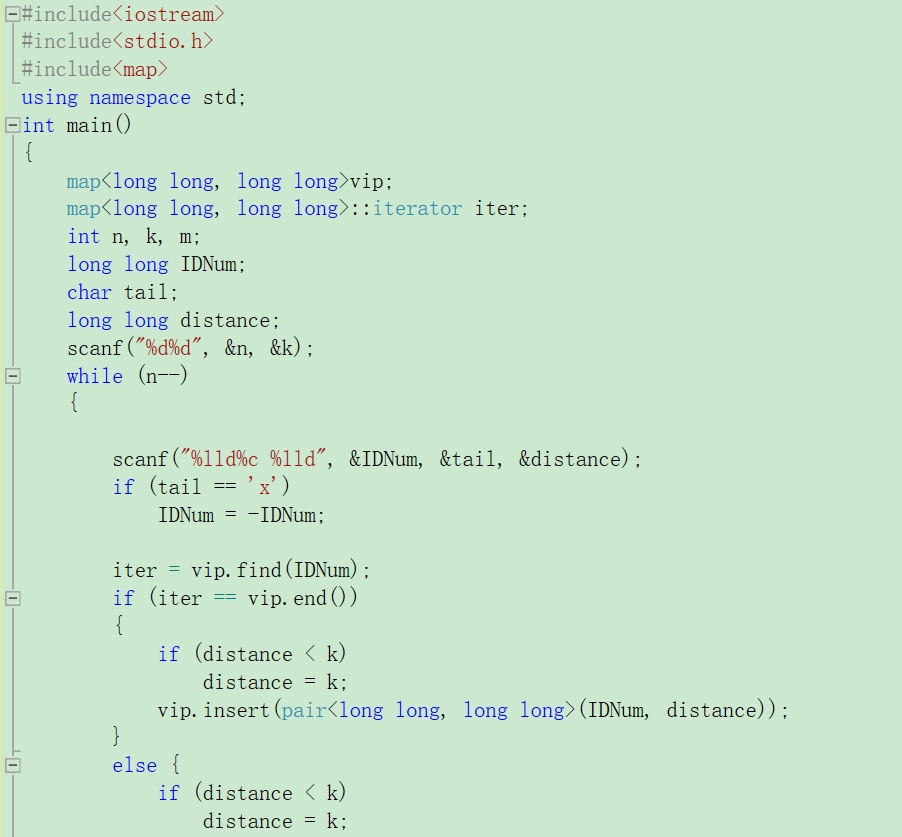
2.3.3本题PTA提交列表说明。

• Q1：当要输入的数据非常多时，出现了超时的现象；
• A1：查找资料发现c++的cin和cout在没有解绑的转态下，其所花时间将近c的scanf和printf的两倍，进行更改。
• Q2：更改后依旧出现超时；
• A2：继续修改可能花时间较大的变量，发现string也会耗时很大，将输入身份证号的string型改成long long型后，在对程序进行小的修改，最后通过了测试。

3、阅读代码

3.1 题目

162. 寻找峰值（来源：力扣）

3.2 解题思路

3.3 代码截图

3.4 学习体会

1.这题的二分查找和我们平常查找二分有点不同，正常的二分查找要求查找表是一个有序表，
而这题中的数据不是一个有序表，而要求查找效率为O(logN)，所以想到二分法。
2.如果自己写代码实现，可能不会想到用二分查找，而是遍历实现，但是时间复杂度过高不
满足题目条件，可能超时，所以在思考题目时要广度思考，择优选择。