acwing10. 有依赖的背包问题
题目描述
有 NN 个物品和一个容量是 VV 的背包。
物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。
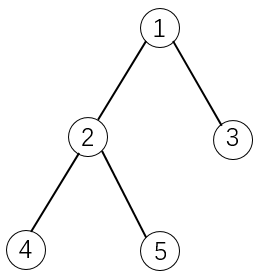
如下图所示：
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。
每件物品的编号是 ii，体积是 vivi，价值是 wiwi，依赖的父节点编号是 pipi。物品的下标范围是 1…N1…N。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N，VN，V，用空格隔开，分别表示物品个数和背包容量。
接下来有 NN 行数据，每行数据表示一个物品。
第 ii 行有三个整数 vi,wi,pivi,wi,pi，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1pi=−1，表示根节点。 数据保证所有物品构成一棵树。输出格式
输出一个整数，表示最大价值。
数据范围
1≤N,V≤1001≤N,V≤100
1≤vi,wi≤1001≤vi,wi≤100父节点编号范围：
- 内部结点：1≤pi≤N1≤pi≤N;
- 根节点 pi=−1pi=−1;
输入样例
5 7 2 3 -1 2 2 1 3 5 1 4 7 2 3 6 2输出样例：
11
dfs+分组背包
分析
树上分组背包问题
对一个节点u，用f[u][j]表示当容量为j的时候，以u为根的子树的最大价值
那么需要求的就是f[root][m]
对每个节点u的话，如何求其f[u][0 ~ m]：
- 首先将u的每个孩子看成一个分组，分组内部按体积划分
- 根据分组背包的思想，需要三重循环
- 第一重
i循环遍历所有分组（即u的所有孩子）- 第二重循环
j遍历所有体积（注意u节点必选，所以体积为m -> m - v[u]，同时注意倒序枚举体积，原理同01背包一维优化类似）- 第三重循环
k就是组内枚举，这里组内按照分给该孩子的体积划分，所以体积为0 -> j
- 第三重循环
- 第二重循环
- 第一重
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int root;
int n, m; //
int f[N][N]; // f[u][j] 表示当前节点为u，体积为j能够有的最大价值
int v[N], w[N]; // v是体积，w是价值
int h[N], e[N], ne[N], idx = 0;
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int son = e[i]; // u的孩子节点son被选中
dfs(son); // 递归找到son的所有f[i][j]
for(int j = m - v[u]; j >= 0; j--) // 当前节点u一定要选，那么剩余体积就是m-v[u]
{
//son组内按照体积大小划分！ k是分给son的体积
for(int k = 0; k <= j; k++)
{
f[u][j] = max(f[u][j], f[son][k] + f[u][j - k]); // son分得了k大小的体积，u还剩j-k
// 注意等式右边的f[u][j], f[u][j-k]都是上一轮求出来的
}
}
}
// 这里也是错的！//for(int j = v[u]; j <= m; j++) f[u][j] = f[u][j-v[u]] + w[u];
// 体积一定是从大到小循环，不能从小到大，因为这里是用晓得更新大的
// 和01背包优化的时候类似！
for(int j = m; j >= v[u]; j--) f[u][j] = f[u][j-v[u]] + w[u]; // 大于等于v[u]的情况都加上u的价值
for(int j = 0; j < v[u]; j++) f[u][j] = 0; // 小于等于v[u]的时候，u节点都不能选，其他孩子更不能选，所以价值是0
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
{
int p;
scanf("%d%d%d", &v[i], &w[i], &p);
if(p == -1) root = i;
else add(p, i); // p->i
}
dfs(root);
printf("%d\n", f[root][m]);
return 0;
}
解法2
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int root;
int n, m; //
int f[N][N]; // f[u][j] 表示当前节点为u，体积为j能够有的最大价值
int v[N], w[N]; // v是体积，w是价值
int h[N], e[N], ne[N], idx = 0;
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
// u节点必选，所以
for(int i = v[u]; i <= m; i++) f[u][i] = w[u];
//
for(int i = h[u]; i != -1; i = ne[i])
{
int son = e[i]; // u的孩子节点son被选中
dfs(son); // 递归找到son的所有f[i][j]
// 体积从大到小
for(int j = m; j >= v[u]; j--)
{
// son组内按照体积大小划分！ k是分给son的体积
// 分给son的体积最大不能超过 j - v[u]，否则不能选择u节点
for(int k = 0; k <= j - v[u]; k++)
{
f[u][j] = max(f[u][j], f[son][k] + f[u][j - k]); // son分得了k大小的体积，u还剩j-k
// 注意等式右边的f[u][j], f[u][j-k]都是上一轮求出来的
}
}
}
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
{
int p;
scanf("%d%d%d", &v[i], &w[i], &p);
if(p == -1) root = i;
else add(p, i); // p->i
}
dfs(root);
printf("%d\n", f[root][m]);
return 0;
}
时间复杂度
参考文章
#include<iostream> #include<vector> using namespace std; int f[110][110];//f[x][v]表达选择以x为子树的物品，在容量不超过v时所获得的最大价值 vector<int> g[110]; int v[110],w[110]; int n,m,root; int dfs(int x) { for(int i=v[x];i<=m;i++) f[x][i]=w[x];//点x必须选，所以初始化f[x][v[x] ~ m]= w[x] for(int i=0;i<g[x].size();i++) { int y=g[x][i]; dfs(y); for(int j=m;j>=v[x];j--)//j的范围为v[x]~m, 小于v[x]无法选择以x为子树的物品 { for(int k=0;k<=j-v[x];k++)//分给子树y的空间不能大于j-v[x],不然都无法选根物品x { f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]); } } } } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { int fa; cin>>v[i]>>w[i]>>fa; if(fa==-1) root=i; else g[fa].push_back(i); } dfs(root); cout<<f[root][m]; return 0; } 作者：yzy0611 链接：https://www.acwing.com/solution/content/8316/ 来源：AcWing 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。思路略区别于dxc的思路
dfs在遍历到 x 结点时，先考虑一定选上根节点 x ，因此初始化f[x][v[x] ~ m] = w[x]在分组背包部分：
j的范围[ m , v[x] ]小于v[x]则没有意义因为连根结点都放不下；k的范围[ 0 , j-v[x] ]，当大于j-v[x]时分给该子树的容量过多，剩余的容量连根节点的物品都放不下了；- 详细思路见代码
