P3916 图的遍历
题目描述
题目描述
给出NN个点,MM条边的有向图,对于每个点vv,求A(v)A(v)表示从点vv出发,能到达的编号最大的点。
输入格式
第1 行,2 个整数N,MN,M。
接下来MM行,每行2个整数U_i,V_iU**i,V**i,表示边(U_i,V_i)(U**i,V**i)。点用1, 2,\cdots,N1,2,⋯,N编号。
输出格式
N 个整数A(1),A(2),\cdots,A(N)A(1),A(2),⋯,A(N)。
输入输出样例
输入 #1复制
4 3 1 2 2 4 4 3输出 #1复制
4 4 3 4说明/提示
• 对于60% 的数据,1 \le N . M \le 10^31≤N.M≤103;
• 对于100% 的数据,1 \le N , M \le 10^51≤N,M≤105。
dfs反向建图 求解
分析
如果反着建图,那么点A能到达点B就成了点B能到达点A。然后从 n 开始倒着枚举每个点
对每个点u,u能dfs到的所有点,其反着也一定能到u,就将能到的点的编号都设置成u;
注意每个点只访问一次就可了
代码
时间复杂度
参考文章
https://blog.csdn.net/weixin_43590232/article/details/105795340
https://www.cnblogs.com/chenjiaxuan/p/10775057.html
当你仔细思考这道题的时候你就会发现:你在从每个点出发去找它能到达的编号最大的点时,每搜到一个点你不能保证它是答案,而那些不是答案的点就浪费了你的宝贵时间
那么,如何避免这个问题呢?
很简单
你可以“倒着”搜:找哪些点能到i,而不是挨个找每个点能到达的编号最大的点
for example:
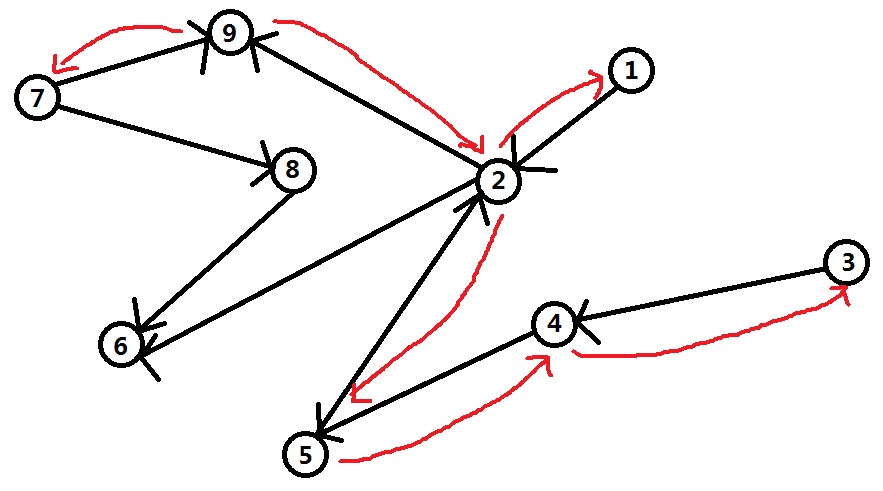
先从最大的点(9号点)开始,沿着能到达它的边反向搜索,搜索到的点能到达的编号最大的点就是它(“9”)
再从第二大的点(8号点)开始,沿着能到达它的边反向搜索,搜索到的点能到达的编号最大的点就是它(“8”)
再从第三大的点(7号点)开始,沿着能到达它的边反向搜索,但是7号点的入度(入度:指向这个点的边的数量叫这个点的入度)为0
再从第四大的点(6号点)开始,沿着能到达它的边反向搜索,搜索到的点能到达的编号最大的点就是它(“6”)
………………(以此类推,直到全图的每一个点都搜索过一遍)
注意:被搜索过的点以后就不需要搜索了
#include<bits/stdc++.h>
using namespace std;
int n,m,ans[100001];
vector<int> adj[100001];
void dfs(int u,int k){
if(ans[u]) return;
ans[u]=k;
for(int i=0;i<adj[u].size();i++){
dfs(adj[u][i],k);
}
}
int main() {
scanf("%d%d",&n,&m);
int a,b;
while(m--){
scanf("%d%d",&a,&b);
adj[b].push_back(a);
}
for(int i=n;i>0;i--) dfs(i,i);
for(int i=1;i<=n;i++){
if(i!=1) printf(" ");
printf("%d",ans[i]);
}
return 0;
}
·