P5318 【深基18.例3】查找文献
题目描述
小K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个(也有可能没有)参考文献的链接指向别的博客文章。小K 求知欲旺盛,如果他看了某篇文章,那么他一定会去看这篇文章的参考文献(如果他之前已经看过这篇参考文献的话就不用再看它了)。
假设洛谷博客里面一共有 n(n\le10^5)n(n≤105) 篇文章(编号为 1 到 nn)以及 m(m\le10^6)m(m≤106) 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章,请帮助小 K 设计一种方法,使小 K 可以不重复、不遗漏的看完所有他能看到的文章。
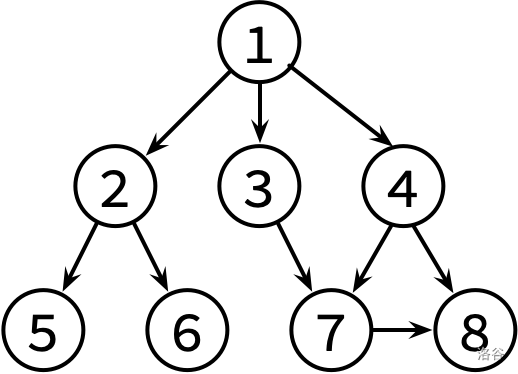
这边是已经整理好的参考文献关系图,其中,文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。
请对这个图分别进行 DFS 和 BFS,并输出遍历结果。如果有很多篇文章可以参阅,请先看编号较小的那篇(因此你可能需要先排序)。
输入格式
共 m+1m+1 行,第 1 行为 2 个数,nn 和 mm,分别表示一共有 n(n\le10^5)n(n≤105) 篇文章(编号为 1 到 nn)以及m(m\le10^6)m(m≤106) 条参考文献引用关系。
接下来 mm 行,每行有两个整数 X,YX,Y 表示文章 X 有参考文献 Y。
输出格式
共 2 行。 第一行为 DFS 遍历结果,第二行为 BFS 遍历结果。
输入输出样例
输入 #1复制
8 9 1 2 1 3 1 4 2 5 2 6 3 7 4 7 4 8 7 8输出 #1复制
1 2 5 6 3 7 8 4 1 2 3 4 5 6 7 8
bfs dfs算法求解
分析
模板dfs,bfs
注意几个点:
- 要求从小到大依次遍历,所以存每个节点指向的点的时候,要从小到大排序,每个节点指向的点用vector存,然后对每个点的vector排序即可
- “目前小 K 已经打开了编号为 1 的一篇文章,请帮助小 K 设计一种方法,使小 K 可以不重复、不遗漏的看完所有他能看到的文章。”:说明只需要从1开始bfs、dfs,其他连通块不需要遍历,1的父节点也不需要遍历
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 100010, M = 1000010;
vector<int> h[N]; // 链表头
bool st[N]; // 是否被访问过
int res[N];
int cnt = 0;
int n, m;
// 从第u个点dfs
void dfs(int u)
{
st[u] = true; // 访问了该节点
// // 已经访问了n个节点
// if(cnt == n)
// {
// //输出
// for(int i = 0; i < n; i++) printf("%d ", res[i]);
// puts("");
// return ;
// }
// u的所有指向的节点
for(int t : h[u])
{
// 如果没有被访问过
if(!st[t])
{
res[cnt++] = t; //记录该节点
dfs(t); //访问t的所有子节点
}
}
}
// bfs不会递归处理的
void bfs(int u)
{
st[u] = true;
queue<int> q;
q.push(u);
while(q.size())
{
int t = q.front();
q.pop();
// 遍历t的所有邻接点
for(int point : h[t])
{
if(!st[point]) // 该点没有出现过
{
st[point] = true;
res[cnt++] = point;
q.push(point);
}
}
}
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 0; i < m; i++)
{
int a, b;
scanf("%d%d", &a, &b);
h[a].push_back(b); // a -> b
}
for(int i = 1; i <= n; i++)
{
sort(h[i].begin(), h[i].end()); // 保证每个点遍历其邻居节点的时候从小到大
}
res[cnt++] = 1;
dfs(1);
for(int i = 0; i < cnt; i++) printf("%d ", res[i]);
puts("");
// // dfs
// for(int i = 1; i <= n; i++)
// {
// if(!st[i]) // 该点没有出现过
// {
// res[cnt++] = i;
// dfs(i);
// }
// }
// bfs
memset(st, 0, sizeof st);
cnt = 0;
res[cnt++] = 1;
bfs(1);
// // 对每个点bfs
// for(int i = 1; i <= n; i++)
// {
// if(!st[i])
// {
// res[cnt++] = i;
// bfs(i);
// }
// }
for(int i = 0; i < cnt; i++) printf("%d ", res[i]);
puts("");
return 0;
}