acwing \871. 约数之和

题目描述

给定 n 个正整数 ai，请你输出这些数的乘积的约数之和，答案对 10^9+7 取模。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式

输出一个整数，表示所给正整数的乘积的约数之和，答案需对 109+7109+7 取模。

数据范围

1≤n≤100
1≤ai≤2×10^9

输入样例：

3
2
6
8

输出样例：

252

试除法求质数 + 快速幂

分析

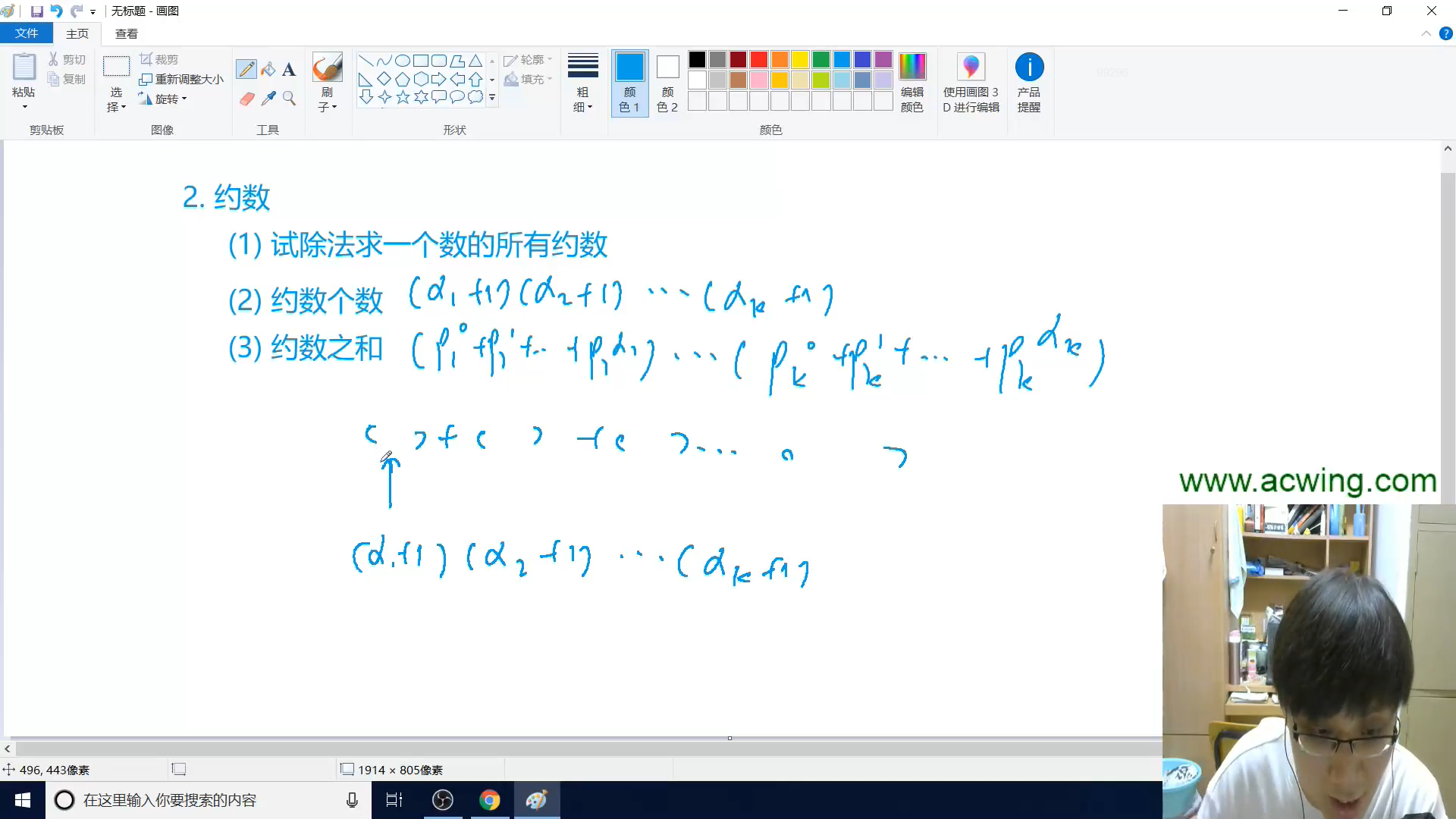
根据上面的公式很好理解，重点就是求出N的每个质因子和其个数

我的做法：使用快速幂来求每个幂

简单写就是上面的那种

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<unordered_map>
using namespace std;

typedef long long ll;

const int mod = 1e9 + 7;
unordered_map<int, int> h; // 用来存每个质数在最后的乘积中出现了多少次

ll ksm(int a, int b, int p)
{
    ll res = 1; 
    ll t = a;
    while(b)
    {
        if(b & 1) res = (res * t) % p;
        t = (t * t) % p;
        b >>= 1;
    }
    return res;
}

int main()
{
    int n;
    scanf("%d", &n);
    while(n--)
    {
        int x;
        scanf("%d", &x);
        for(int i = 2; i <= x/i; i++)
        {
            if(x % i == 0)
            {
                int cnt = 0;
                while(x % i == 0)
                {
                    cnt++;
                    x /= i;
                }
                h[i] += cnt;
            }
            
        }
        if(x > 1) h[x] += 1;
    }
    
    // for(auto item : h) cout << item.first << " " << item.second << endl;
    // return 0;
    
    
    ll res = 1;
    /*for(auto item : h)
    {
         // a^0 + a^1 + a^2 + a^h[a]
        ll t = 0;
        for(int j = 0; j <= item.second; j++)
        {
            t = (t + ksm(item.first, j, mod)) % mod;
        }
        res = (res * t) % mod;
    }*/
    
    for(auto item : h)
    {
        int a = item.first, b = item.second;
        ll t = 1;
        while(b --) t = (t * a + 1) % mod;
        res = (res * t) % mod;
    }
    printf("%lld\n", res);
    return 0;
}

时间复杂度

参考文章