数据结构：图及其邻接矩阵与邻接表表示

图

六度空间理论

图中两个顶点若要联系，最多通过6个结点便可以完成 。

基本概念

• 图用于表示“多对多”的关系。

• 包含

• 一组顶点：通常用V (Vertex) 表示顶点集合

• 一组边：通常用E (Edge) 表示边的集合

• 边是顶点对：(v, w) E ，其中v, w V

• 有向边< v, w> 表示从v指向w的边（单行线）

  

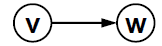
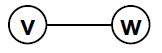
• 不考虑重边和自回路

  • 重边：两个顶点之间有两条边。
  • 自回路：一个顶点的边指向自己。
    

抽象数据类型定义

• 类型名称：图（Graph）
• 数据对象集：G(V,E)由一个非空的有限顶点集合V和一个有限边集合E组成。
• 操作集：对于任意图G  Graph，以及v  V, e  E
• Graph Create()：建立并返回空图；
• Graph InsertVertex(Graph G, Vertex v)：将v插入G；
• Graph InsertEdge(Graph G, Edge e)：将e插入G；
• void DFS(Graph G, Vertex v)：从顶点v出发深度优先遍历图G；
• void BFS(Graph G, Vertex v)：从顶点v出发宽度优先遍历图G；
• void ShortestPath(Graph G, Vertex v, int Dist[])：计
  算图G中顶点v到任意其他顶点的最短距离；
• void MST(Graph G)：计算图G的最小生成树；

怎么在程序中表示一个图

• 对顶点进行编号。
• 顶点序号所对应在邻接矩阵中的值为1。
• 因为没有自回路，所以对角线全为0。
• 无向图为对称矩阵。
  

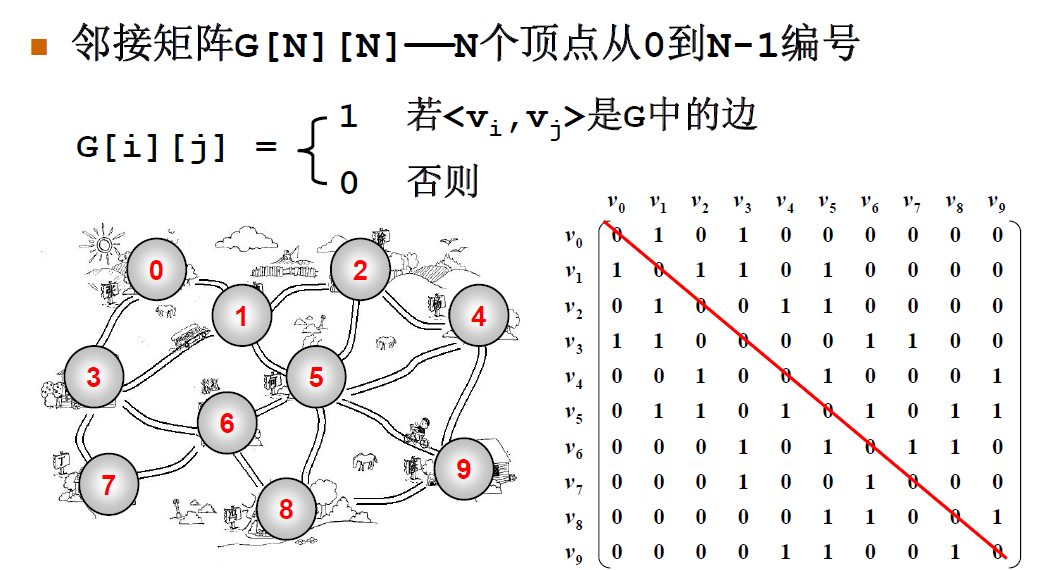
问题：对于无向图的存储，怎样可以省一半空间？

• 用一个长度为N(N+1)/2的1维数组A存储{G00,G10,G11,……,Gn-1 0,…,Gn-1 n-1}，则Gij在A中对应的下标是：(i*(i+1)/2+j)。
  -对于网络，只要把G[i][j]的值定义为边<vi,vj>的权重即可。
  

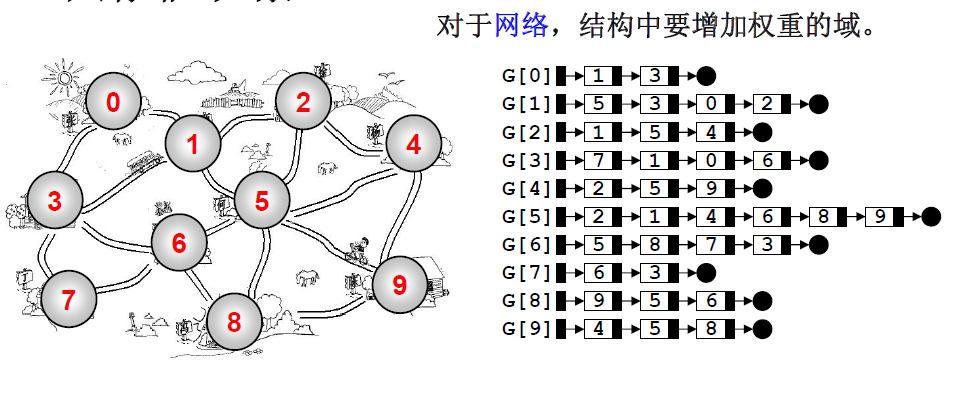
邻接矩阵—— 有什么好处？

• 直观、简单、好理解
• 方便检查任意一对顶点间是否存在边
• 方便找任一顶点的所有“邻接点”（有边直接相连的顶点）
• 方便计算任一顶点的“度”（从该点发出的边数为“出
  度”，指向该点的边数为“入度”）
• 无向图：对应行（或列）非0元素的个数
• 有向图：对应行非0元素的个数是“出度”；对应列非0元素的
  个数是“入度”

邻接矩阵—— 有什么不好？

• 浪费空间—— 存稀疏图（点很多而边很少）有大量无效元素
• 对稠密图（特别是完全图）还是很合算的
• 浪费时间—— 统计稀疏图中一共有多少条边

邻接表

• G[N]为指针数组，对应矩阵每行一个链表，只存非0元素

邻接矩阵—— 有什么好处？

• 方便找任一顶点的所有“邻接点”
• 节约稀疏图的空间：需要N个头指针+2E（每个节点至少两个域）
• 方便计算任一顶点的“度”？：对无向图：是的，对又想吐只能计算出度，需要构造“逆邻接表”计算入度。

邻接矩阵—— 有什么不好？

• 不方便检查任意一对顶点间是否存在边。

代码实现

• 设定初始参数，最大值和权值顶点数
• 设定边结点，用于连接顶点。
• 设定图结点，建立顶点数，边数，表示关系的邻接矩阵。
• 设定插入函数，把边插入到图当中。

设定参数

• 设定INFINITY为最大值，便于权值的比较。

#define MaxVertexNum 100    /* 最大顶点数设为100 */
#define INFINITY 65535        /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
typedef int WeightType;        /* 边的权值设为整型 */
typedef char DataType;        /* 顶点存储的数据类型设为字符型 */
 

设定边结点

• 包括边结点、边结点的指针、边连接的两个顶点和边的权重。

/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
    Vertex V1, V2;      /* 有向边<V1, V2> */
    WeightType Weight;  /* 权重 */
};
typedef PtrToENode Edge;
      

设定图结点

• 包括图结点、图结点的指针、包含的顶点数、边数、图的邻接矩阵、顶点存储的数据。

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;  /* 顶点数 */
    int Ne;  /* 边数   */
    WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
    DataType Data[MaxVertexNum];      /* 存顶点的数据 */
    /* 注意：很多情况下，顶点无数据，此时Data[]可以不用出现 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
 

创建一个图

• 创建一个图结点并将顶点初始化，返回指针。

 
MGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
    Vertex V, W;
    MGraph Graph;
     
    Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    /* 初始化邻接矩阵 */
    /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
    for (V=0; V<Graph->Nv; V++)
        for (W=0; W<Graph->Nv; W++)  
            Graph->G[V][W] = INFINITY;
             
    return Graph; 
}
   

将边插入到顶点当中

• 接受一个边结点，把对应值的关系储存。
• 若是无向图要储存两次。

     
void InsertEdge( MGraph Graph, Edge E )
{
     /* 插入边 <V1, V2> */
     Graph->G[E->V1][E->V2] = E->Weight;    
     /* 若是无向图，还要插入边<V2, V1> */
     Graph->G[E->V2][E->V1] = E->Weight;
}
 

建立图

MGraph BuildGraph()
{
    MGraph Graph;
    Edge E;
    Vertex V;
    int Nv, i;
     
    scanf("%d", &Nv);   /* 读入顶点个数 */
    Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ 
     
    scanf("%d", &(Graph->Ne));   /* 读入边数 */
    if ( Graph->Ne != 0 ) { /* 如果有边 */ 
        E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */ 
        /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
        for (i=0; i<Graph->Ne; i++) {
            scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
            /* 注意：如果权重不是整型，Weight的读入格式要改 */
            InsertEdge( Graph, E );
        }
    } 
 
    /* 如果顶点有数据的话，读入数据 */
    for (V=0; V<Graph->Nv; V++) 
        scanf(" %c", &(Graph->Data[V]));
 
    return Graph;
}