数据结构：判断是否为同一棵二叉搜索树

问题

• 给定一个插入序列就可以唯一确定一棵二叉搜索树。然而，一棵给定的二叉搜索树却可以由多种不同的插入序列得到。
• 例如，按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树，都得到一样的结果。
• 问题：对于输入的各种插入序列，你需要判断它们是否能生成一样的二叉搜索树。
  

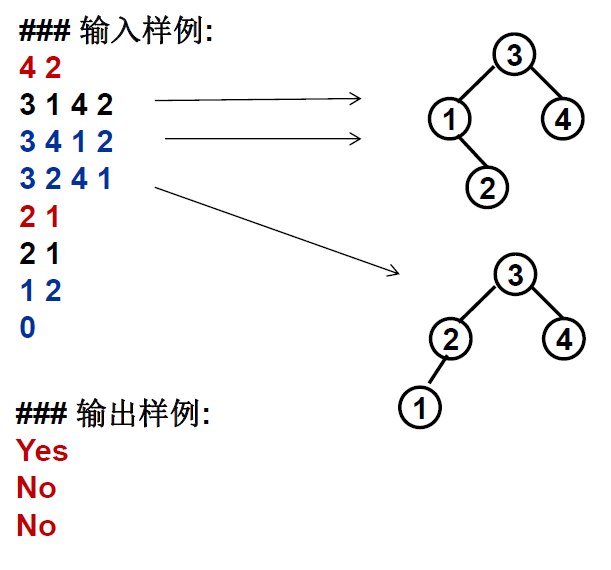
输入输出示例

三种求解思路

1. 分别建两棵搜索树的判别方法：
   根据两个序列分别建树，再判别树是否一样。

2. 不建树的判别方法：根据根结点，把序列按左右子树分为两个分序列，再进行比较
   3 1 2 4 vs 3 4 1 2
   {1 2} 3 {4} {1 2} 3 {4}
   3 1 2 4 vs 3 2 4 1

3. 建一棵树，再判别其他序列是否与该树一致：

   1. 搜索树表示
   2. 建搜索树T
   3. 判别一序列是否与搜索树T一致

搜索树表示

• flag：标记序列中是否有这个结点

typedef struct TreeNode *Tree;
struct TreeNode {
int v;
Tree Left, Right;
int flag;
};

主函数部分

int main() { 
对每组数据
1 读入N和L
2 根据第一行序列建树T
3 依据树T分别判别后面的L个序列是否能与T形成同一搜索树并输出结果 return 0; }

需要设计的主要函数：

• 读数据建搜索树T
• 判别一序列是否与T构成一样的搜索树

int main()
{ int N, L, i;
Tree T;
scanf("%d", &N);
while (N) {
scanf("%d", &L);
T = MakeTree(N);
for (i=0; i<L; i++) {
if (Judge(T, N)) printf("Yes\n");
else printf("No\n");
ResetT(T); /*清除T中的标记flag*/
}
FreeTree(T);
scanf("%d", &N);
}
return 0;
}

建搜索树

建立搜索树

Tree MakeTree( int N )
{ Tree T;
int i, V;
scanf("%d", &V);
T = NewNode(V);
for (i=1; i<N; i++) {
scanf("%d", &V);
T = Insert(T, V);
}
return T;
}

插入操作

• 结点指针为空时，新建一个结点
• 结点非空，按照大小关系进入搜索树

Tree Insert( Tree T, int V )
{
if ( !T ) T = NewNode(V);
else {
if ( V>T->v )
T->Right = Insert( T->Right, V );
else
T->Left = Insert( T->Left, V );
}
return T;
}

建立新结点

• 初始化：动态创建结点，结点值，左右结点值

Tree NewNode( int V )
{ Tree T = (Tree)malloc(sizeof(struct TreeNode));
T->v = V;
T->Left = T->Right = NULL;
T->flag = 0;
return T;
}

判别序列是否一致

方法：在树T中按顺序搜索序列3 2 4 1中的每个数

• 如果每次搜索所经过的结点在前面均出现过，则一致

• 否则（某次搜索中遇到前面未出现的结点），则不一致
  

• 分为两种情况：该结点与序列中的一致（flag=0）或不一致（flag=1）

• 到达一个结点，若未遍历过，则判断是否与序列的一致。

• 若不一致，则返回0，一致则标记为1。

• 若遍历过，则判断该结点值与序列中的值的大小关系，进入下一个子树。

int check ( Tree T, int V )
{
if ( T->flag ) {
if ( V<T->v ) return check(T->Left, V);
else if ( V>T->v ) return check(T->Right, V);
else return 0;
}
else {
if ( V==T->v ) {
T->flag = 1;
return 1;
}
else return 0;
}
}

int Judge( Tree T, int N )
{
int i, V, flag = 0;
/* flag: 0代表目前还一致，1代表已经不一致*/
scanf("%d", &V);
if ( V!=T->v ) flag = 1;
else T->flag = 1;
for (i=1; i<N; i++) {
scanf("%d", &V);
if ( (!flag) && (!check(T, V)) ) flag = 1;
}
if (flag) return 0;
else return 1;
}

• 递归重置

void ResetT ( Tree T ) /* 清除T中各结点的flag标记 */
{
if (T->Left) ResetT(T->Left);
if (T->Right) ResetT(T->Right);
T->flag = 0;
}

• 递归重置

void FreeTree ( Tree T ) /* 释放T的空间 */
{
if (T->Left) FreeTree(T->Left);
if (T->Right) FreeTree(T->Right);
free(T);
}